Sześć funkcji trygonometrycznych to sin, cos, tan, cosec, sec i cot.
Spróbujmy znaleźć \(\angle A\) w podanym trójkącie.
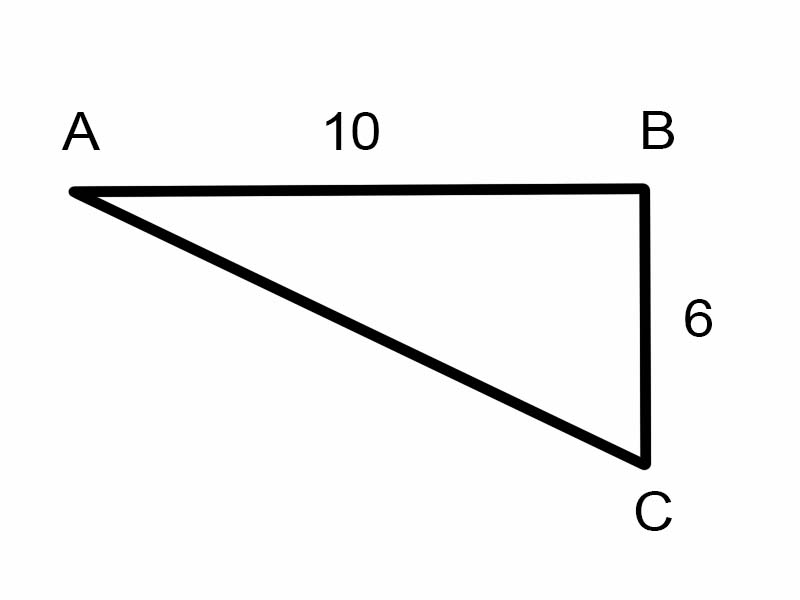
\(\tan A = \frac{6}{10}\)
Ale to nie jest pomocne w znalezieniu miary \(\angle A\)
Musimy znaleźć nowe narzędzie matematyczne do rozwiązywania takich problemów. Funkcje sinus, cosinus i tangens przyjmują kąty i podają stosunki boków. Ale potrzebujemy funkcji, które przyjmują stosunki boków i podają kąty, dlatego wprowadzamy odwrotne funkcje trygonometryczne .
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Oceń za pomocą kalkulatora]
Jeżeli znana jest długość dwóch boków, miarę kąta można wyznaczyć korzystając z odwrotnej funkcji trygonometrycznej.
\(\sin^{-1}x \textrm{ Lub } \arcsin x\) jest funkcją odwrotną do sinusa.
\(\cos^{-1}x \textrm{ Lub } \arccos x \) jest funkcją odwrotną do cos.
\(\tan^{-1}x \textrm{ Lub } \arctan x\) jest odwrotną funkcją tangensa.
\(\csc^{-1}x \) lub arccsc x jest funkcją odwrotną csc.
\(\sec^{-1}x \) lub arcsec x jest odwrotną funkcją sec.
\(cot^{-1}x \) lub arccot x jest odwrotną funkcją cot.
Niech w trójkącie \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [jako \(\sin\theta = \) Prostopadła ∕ Przeciwprostokątna]
Możemy zapisać jako \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Możemy wyznaczyć wartości stosunków trygonometrycznych, gdy \(\theta\) jest podane jako odwrotność zgodnie z poniższą tabelą :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Przykład 1: Drabina oparta o ścianę tworzy kąt θ z podłożem. Podstawa drabiny znajduje się 3 metry od ściany, a drabina ma 5 metrów długości. Znajdź θ.
Rozwiązanie:
Ponieważ mamy przeciwprostokątną (5 m) i przyległy bok (3 m), używamy funkcji cosinus:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Użyj kalkulatora, aby wyprowadzić wartość θ, \(\theta \approx 53.13^{\circ}\)
Przykład 2: Oblicz \(cos^{−1}(\frac{-1}{2}) \)
Rozwiązanie:
Korzystając z własności odbicia: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Podstawienie \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Przykład 3: Oblicz \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Rozwiązanie:
Korzystając z tożsamości: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
W przypadku funkcji trygonometrycznych odwrotnych dziedzina odnosi się do zbioru wartości wejściowych (wartości x), dla których funkcja jest zdefiniowana, a zakres odnosi się do zbioru wartości wyjściowych (wartości y), które funkcja może przyjąć.
Oto dziedziny i zakresy sześciu odwrotnych funkcji trygonometrycznych:
| Dziedzina | funkcji | Zakres |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |