As seis funções trigonométricas são sin, cos, tan, cosec, sec e cot.
Vamos tentar encontrar \(\angle A\) no triângulo dado.
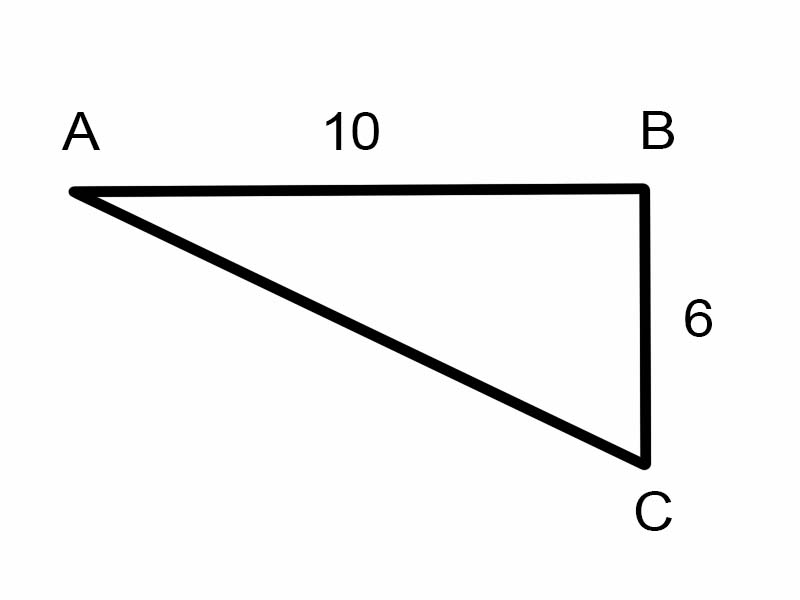
\(\tan A = \frac{6}{10}\)
Mas isso não ajuda a encontrar a medida do \(\angle A\)
Precisamos encontrar uma nova ferramenta matemática para resolver problemas como esses. Funções seno, cosseno e tangente pegam ângulos e dão razões laterais. Mas precisamos de funções que pegam razões laterais e dão ângulos e, portanto, funções trigonométricas inversas são introduzidas.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Calcule com a calculadora]
Se o comprimento de dois lados for conhecido, as medidas dos ângulos podem ser determinadas usando a função trigonométrica inversa.
\(\sin^{-1}x \textrm{ ou } \arcsin x\) é uma função seno inversa.
\(\cos^{-1}x \textrm{ ou } \arccos x \) é a função cos inversa.
\(\tan^{-1}x \textrm{ ou } \arctan x\) é uma função tan inversa.
\(\csc^{-1}x \) ou arccsc x é a função csc inversa.
\(\sec^{-1}x \) ou arcsec x é a função sec inversa.
\(cot^{-1}x \) ou arccot x é a função cot inversa.
Em um triângulo seja \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [como \(\sin\theta = \) Perpendicular∕ Hipotenusa]
Podemos escrever como \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Podemos derivar o valor das razões trigonométricas quando \(\theta\) é dado como inverso de acordo com a tabela abaixo :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Exemplo 1: Uma escada se apoia em uma parede, formando um ângulo θ com o chão. A base da escada está a 3 metros de distância da parede, e a escada tem 5 metros de comprimento. Encontre θ.
Solução:
Como temos a hipotenusa (5 m) e o cateto adjacente (3 m), usamos a função cosseno:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Use a calculadora para derivar o valor de θ, \(\theta \approx 53.13^{\circ}\)
Exemplo 2: Avalie \(cos^{−1}(\frac{-1}{2}) \)
Solução:
Usando a propriedade de reflexão: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Substituindo \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Exemplo 3: Avalie \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Solução:
Usando a identidade: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Em funções trigonométricas inversas , o domínio se refere ao conjunto de valores de entrada (valores x) para os quais a função é definida, e o intervalo se refere ao conjunto de valores de saída (valores y) que a função pode assumir.
Aqui estão os domínios e intervalos das seis funções trigonométricas inversas:
| Faixa | de domínio | de função |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |