Шесть тригонометрических функций — это sin, cos, tan, cosec, sec и cot.
Попробуем найти \(\angle A\) в данном треугольнике.
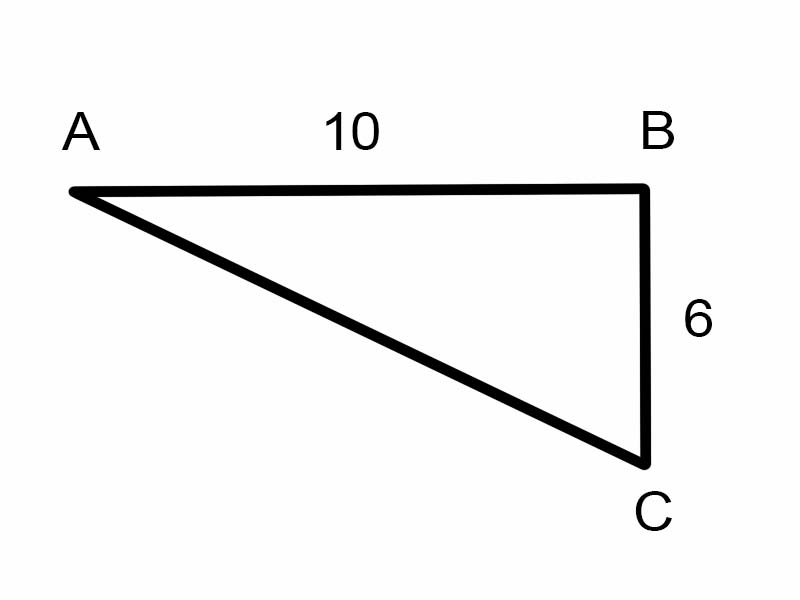
\(\tan A = \frac{6}{10}\)
Но это не поможет найти меру \(\angle A\)
Нам нужно найти новый математический инструмент для решения таких задач. Функции синуса, косинуса и тангенса берут углы и дают соотношения сторон. Но нам нужны функции, которые берут соотношения сторон и дают углы, и поэтому вводятся обратные тригонометрические функции .
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Оценить с помощью калькулятора]
Если известны длины двух сторон, то угловые меры можно определить с помощью обратной тригонометрической функции.
\(\sin^{-1}x \textrm{ или } \arcsin x\) — функция арксинуса.
\(\cos^{-1}x \textrm{ или } \arccos x \) — обратная функция cos.
\(\tan^{-1}x \textrm{ или } \arctan x\) — функция, обратная тангенсу.
\(\csc^{-1}x \) или arccsc x — обратная csc функция.
\(\sec^{-1}x \) или arcsec x — обратная функция sec.
\(cot^{-1}x \) или arccot x — обратная функция cot.
В треугольнике пусть \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [так как \(\sin\theta = \) Перпендикуляр∕ Гипотенуза]
Мы можем записать как \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Мы можем вывести значение тригонометрических соотношений, когда \(\theta\) задано как обратное, согласно приведенной ниже таблице :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Пример 1: Лестница прислонена к стене, образуя угол θ с землей. Основание лестницы находится на расстоянии 3 метров от стены, а длина лестницы составляет 5 метров. Найдите θ.
Решение:
Поскольку у нас есть гипотенуза (5 м) и прилежащий катет (3 м), используем функцию косинуса:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Используйте калькулятор, чтобы вывести значение θ, \(\theta \approx 53.13^{\circ}\)
Пример 2: Оценить \(cos^{−1}(\frac{-1}{2}) \)
Решение:
Используя свойство отражения: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Подставляя \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Пример 3: Оценить \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Решение:
Используя тождество: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
В обратных тригонометрических функциях домен относится к набору входных значений (значений x), для которых определена функция, а диапазон относится к набору выходных значений (значений y), которые может принимать функция.
Вот области определения и диапазоны шести обратных тригонометрических функций:
| Область | области | функции |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |