Gjashtë funksionet trigonometrike janë sin, cos, tan, cosec, sec dhe cot.
Le të përpiqemi të gjejmë \(\angle A\) në trekëndëshin e dhënë.
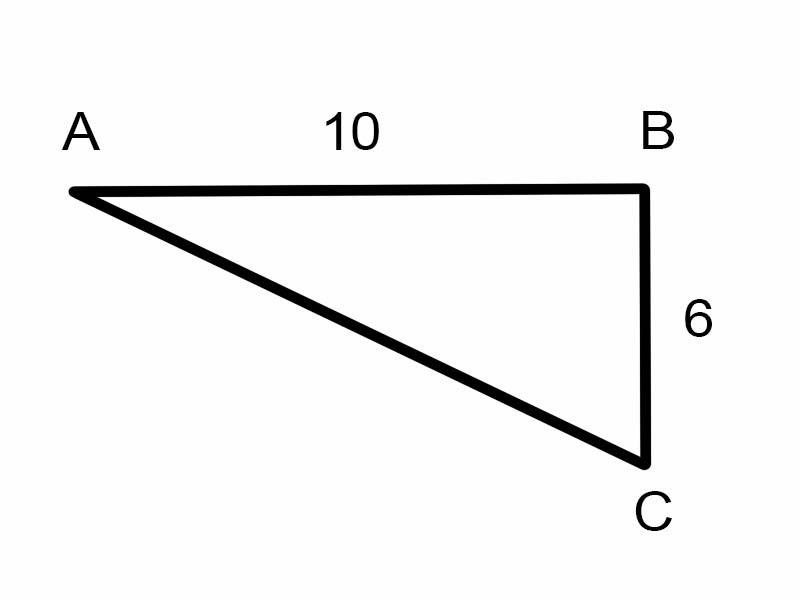
\(\tan A = \frac{6}{10}\)
Por kjo nuk është e dobishme për të gjetur masën e \(\angle A\)
Ne duhet të gjejmë një mjet të ri matematikor për të zgjidhur probleme si këto. Funksionet sinus, kosinus dhe tangjente marrin kënde dhe japin raportet anësore. Por ne kemi nevojë për funksione që marrin raportet anësore dhe japin kënde dhe për këtë arsye futen funksionet trigonometrike të anasjellta .
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Vlerëso me kalkulatorin]
Nëse dihet gjatësia e dy brinjëve, matjet e këndit mund të përcaktohen duke përdorur funksionin trigonometrik të anasjelltë.
\(\sin^{-1}x \textrm{ ose } \arcsin x\) është funksion sinus i anasjelltë.
\(\cos^{-1}x \textrm{ ose } \arccos x \) është funksion i anasjelltë cos.
\(\tan^{-1}x \textrm{ ose } \arctan x\) është funksion i anasjelltë tan.
\(\csc^{-1}x \) ose arccsc x është funksion invers csc.
\(\sec^{-1}x \) ose arcsec x është funksion invers sec.
\(cot^{-1}x \) ose arccot x është funksion invers i shtratit.
Në një trekëndësh leni \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [si \(\sin\theta = \) Hipotenuzë pingul∕]
Mund të shkruajmë si \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Ne mund të nxjerrim vlerën e raporteve trigonometrike kur \(\theta\) jepet si e anasjelltë sipas tabelës së mëposhtme :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Shembulli 1: Një shkallë mbështetet pas një muri, duke krijuar një kënd θ me tokën. Baza e shkallës është 3 metra larg murit, dhe shkalla është e gjatë 5 metra. Gjeni θ.
Zgjidhja:
Meqenëse kemi hipotenuzën (5 m) dhe anën ngjitur (3 m), përdorim funksionin kosinus:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Përdorni makinën llogaritëse për të nxjerrë vlerën e θ, \(\theta \approx 53.13^{\circ}\)
Shembulli 2: Vlerësoni \(cos^{−1}(\frac{-1}{2}) \)
Zgjidhja:
Duke përdorur vetinë e reflektimit: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Duke zëvendësuar \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Shembulli 3: Vlerësoni \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Zgjidhja:
Duke përdorur identitetin: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Në funksionet trigonometrike të anasjellta , domeni i referohet grupit të vlerave hyrëse (x-vlerat) për të cilat është përcaktuar funksioni, dhe diapazoni i referohet grupit të vlerave dalëse (y-vlerat) që mund të marrë funksioni.
Këtu janë domenet dhe vargjet e gjashtë funksioneve trigonometrike të anasjellta:
| Gama | e domenit | të funksionit |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(-\infty \le x \le \infty\) | \(y = \cot^{-1}x\) | \(0 \lt y \lt {\pi}\) |