Back to the topics list

omvända trigonometriska funktioner

De sex trigonometriska funktionerna är sin, cos, tan, cosec, sec och cot.

Låt oss försöka hitta \(\angle A\) i den givna triangeln.

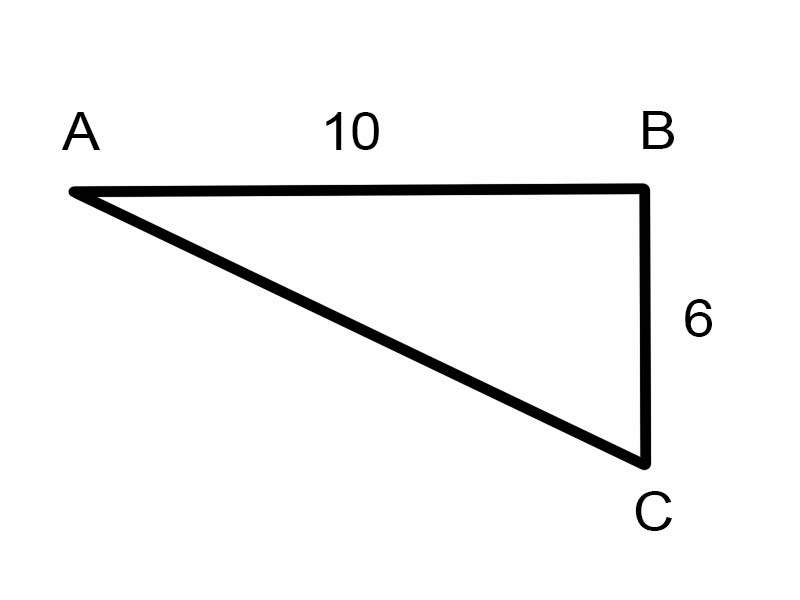
\(\tan A = \frac{6}{10}\)

Men det här är inte användbart för att hitta måttet på \(\angle A\)

Vi måste hitta ett nytt matematiskt verktyg för att lösa problem som dessa. Sinus, Cosinus och Tangent funktioner tar vinklar och ger sidoförhållanden. Men vi behöver funktioner som tar sidförhållanden och ger vinklar och därför introduceras omvända trigonometriska funktioner .

\(\tan A = \frac{6}{10}\)

\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)

A = 30,96° [Utvärdera med kalkylatorn]

Om längden på två sidor är känd kan vinkelmått bestämmas med hjälp av den inversa trigonometriska funktionen.

\(\sin^{-1}x \textrm{ eller } \arcsin x\) är invers sinusfunktion.

\(\cos^{-1}x \textrm{ eller } \arccos x \) är invers cos-funktion.

\(\tan^{-1}x \textrm{ eller } \arctan x\) är invers tan-funktion.

\(\csc^{-1}x \) eller arccsc x är invers csc-funktion.

\(\sec^{-1}x \) eller arcsec x är invers sek-funktion.

\(cot^{-1}x \) eller arccot ​​x är invers cot-funktion.

Relation mellan trigonometri och invers trigonometrifunktioner

Låt \(\sin \theta = x\) i en triangel

⇒ \(\sin \theta = {x \over 1}\) [som \(\sin\theta = \) Vinkelrät∕ Hypotenus]

Vi kan skriva som \({x \over 1} = \frac{AB}{AC}\)

\(AC^2 = AB^2 + BC^2\)

⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)

Vi kan härleda värdet av trigonometriska förhållanden när \(\theta\) ges som invers enligt nedanstående tabell :
1. \(\theta = \sin^{-1}x\)

2. \(\theta = \cos^{-1}x\)

3. \(\theta = \tan^{-1}x\)

Kan du nu härleda värdena för \(\csc^{-1} x\) , \(\sec^{-1}x\) , \(\cot^{-1}x\) ?

Förhållandet mellan inversa trigonometriska funktioner:

\(\sin^{-1}(-x) = - \sin^{-1} x\)

\(\tan^{-1}(-x) = - \tan^{-1} x\)

\(\csc^{-1}(-x) = - \csc^{-1} x\)

\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)

\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)

\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)

\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)

\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)

\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)

\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)

\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)

\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)

\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)

Exempel:

Exempel 1: En stege lutar sig mot en vägg och bildar en vinkel θ mot marken. Stegens bas är 3 meter från väggen och stegen är 5 meter lång. Hitta θ.

Lösning:
Eftersom vi har hypotenusan (5 m) och den intilliggande sidan (3 m), använder vi cosinusfunktionen:

\(\cos \theta = {3 \over 5}\)

\(\theta = \cos^{-1} ({3 \over 5})\) Använd kalkylatorn för att härleda värdet på θ, \(\theta \approx 53.13^{\circ}\)

Exempel 2: Utvärdera \(cos⁡^{−1}(\frac{-1}{2}) \)

Lösning:

Använda reflektionsegenskapen: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)

Ersätter \( x=\frac{1}{2} \)

\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)

Exempel 3: Utvärdera \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)

Lösning:

Använda identiteten: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)

\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)

Domän och omfång av inversa trigonometriska funktioner

I inversa trigonometriska funktioner hänvisar domänen till den uppsättning ingångsvärden (x-värden) som funktionen är definierad för, och intervallet hänvisar till den uppsättning utdatavärden (y-värden) som funktionen kan ta.

Här är domänerna och intervallen för de sex inversa trigonometriska funktionerna: