Vitendaji sita vya trigonometric ni sin, cos, tan, cosec, sec na cot.
Wacha tujaribu kupata \(\angle A\) katika pembetatu iliyotolewa.
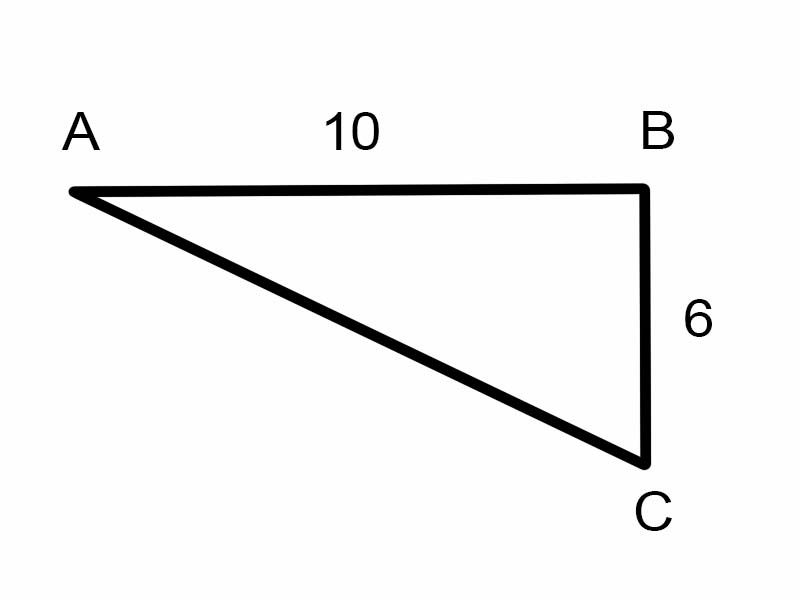
\(\tan A = \frac{6}{10}\)
Lakini hii haisaidii kupata kipimo cha \(\angle A\)
Tunahitaji kutafuta zana mpya ya hisabati ili kutatua matatizo kama haya. Vitendaji vya Sine, Cosine na Tangent huchukua pembe na kutoa uwiano wa upande. Lakini tunahitaji chaguo za kukokotoa ambazo huchukua uwiano wa upande na kutoa pembe na kwa hivyo vitendaji Inverse Trigonometric vinaanzishwa.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96° [Tathmini kwa kutumia kikokotoo]
Ikiwa urefu wa pande mbili unajulikana, hatua za pembe zinaweza kuamua kwa kutumia kazi ya trigonometric inverse.
\(\sin^{-1}x \textrm{ au } \arcsin x\) ni kitendakazi kinyume cha sine.
\(\cos^{-1}x \textrm{ au } \arccos x \) ni kitendakazi kinyume cha cos.
\(\tan^{-1}x \textrm{ au } \arctan x\) ni kitendakazi kinyume cha tani.
\(\csc^{-1}x \) au arcsc x ni kitendakazi kinyume cha csc.
\(\sec^{-1}x \) au arcsec x ni chaguo la kukokotoa la sec kinyume.
\(cot^{-1}x \) au arccot x ni utendakazi kinyume cha kitanda.
Katika pembetatu acha \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [kama \(\sin\theta = \) Perpendicular∕ Hypotenuse]
Tunaweza kuandika kama \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Tunaweza kupata thamani ya uwiano wa trigonometric wakati \(\theta\) imetolewa kama kinyume kulingana na jedwali hapa chini :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Mfano 1: Ngazi inaegemea ukuta, na kutengeneza pembe θ na ardhi. Msingi wa ngazi ni mita 3 kutoka kwa ukuta, na ngazi ni mita 5 kwa muda mrefu. Tafuta θ.
Suluhisho:
Kwa kuwa tuna hypotenuse (m 5) na upande wa karibu (m 3), tunatumia kazi ya cosine:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Tumia kikokotoo kupata thamani ya θ, \(\theta \approx 53.13^{\circ}\)
Mfano wa 2: Tathmini \(cos^{−1}(\frac{-1}{2}) \)
Suluhisho:
Kwa kutumia sifa ya kuakisi: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Inabadilisha \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Mfano wa 3: Tathmini \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Suluhisho:
Kwa kutumia kitambulisho: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Katika kinyume cha chaguo za kukokotoa za trigonometriki , kikoa kinarejelea seti ya thamani za ingizo (thamani x) ambazo utendakazi wake umebainishwa, na safu inarejelea seti ya thamani za matokeo (y-thamani) ambazo chaguo la kukokotoa linaweza kuchukua.
Hapa kuna vikoa na safu za vitendakazi sita kinyume cha trigonometriki:
| Safu ya | Kikoa cha | Utendaji |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |