ฟังก์ชันตรีโกณมิติทั้ง 6 ตัวคือ sin, cos, tan, cosec, sec และ cot
มาลองหา \(\angle A\) ในรูปสามเหลี่ยมที่กำหนดให้กันดีกว่า
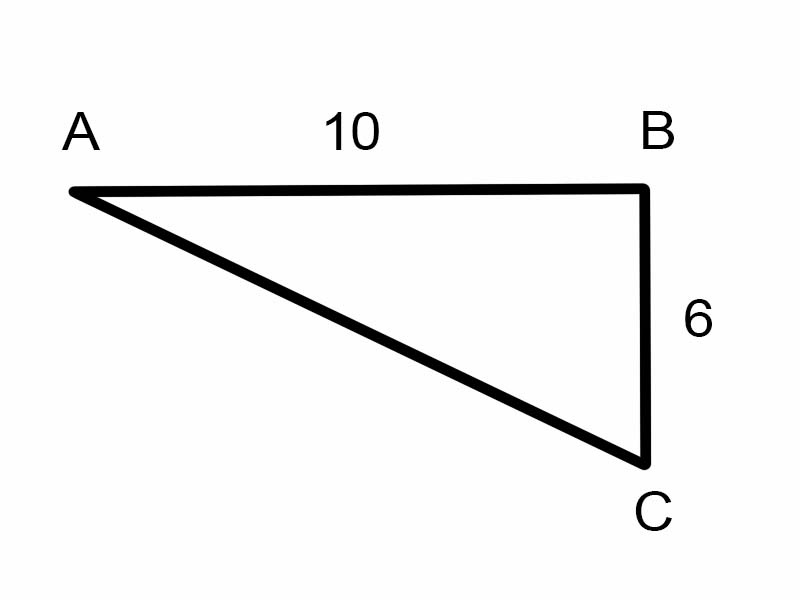
\(\tan A = \frac{6}{10}\)
แต่สิ่งนี้ไม่ช่วยหาขนาดของ \(\angle A\)
เราจำเป็นต้องค้นหาเครื่องมือทางคณิตศาสตร์ใหม่เพื่อแก้ปัญหาเหล่านี้ ฟังก์ชันไซน์ โคไซน์ และแทนเจนต์ใช้ค่ามุมและให้ค่าอัตราส่วนด้าน แต่เราต้องการฟังก์ชันที่ใช้ค่าอัตราส่วนด้านและให้ค่ามุม ดังนั้นจึงมีการแนะนำ ฟังก์ชันตรีโกณมิติผกผัน
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96° [ประเมินด้วยเครื่องคิดเลข]
หากทราบความยาวด้านสองด้านแล้ว ก็สามารถกำหนดขนาดมุมได้โดยใช้ฟังก์ชันตรีโกณมิติผกผัน
\(\sin^{-1}x \textrm{ หรือ } \arcsin x\) เป็นฟังก์ชันไซน์ผกผัน
\(\cos^{-1}x \textrm{ หรือ } \arccos x \) เป็นฟังก์ชัน cos ผกผัน
\(\tan^{-1}x \textrm{ หรือ } \arctan x\) เป็นฟังก์ชันผกผันของ tan
\(\csc^{-1}x \) หรือ arccsc x เป็นฟังก์ชันผกผันของ csc
\(\sec^{-1}x \) หรือ arcsec x เป็นฟังก์ชัน sec ผกผัน
\(cot^{-1}x \) หรือ arccot x เป็นฟังก์ชันผกผันของ cot
ในรูปสามเหลี่ยม ให้ \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [เนื่องจาก \(\sin\theta = \) ตั้งฉาก∕ ด้านตรงข้ามมุมฉาก]
เราสามารถเขียนเป็น \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
เราสามารถหาค่าอัตราส่วนตรีโกณมิติได้เมื่อกำหนดให้ \(\theta\) เป็นค่าผกผันตามตารางด้านล่าง :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
ตัวอย่างที่ 1: บันไดเอียงพิงกำแพง ทำมุม θ กับพื้น ฐานของบันไดอยู่ห่างจากกำแพง 3 เมตร และบันไดยาว 5 เมตร จงหา θ
สารละลาย:
เนื่องจากเรามีด้านตรงข้ามมุมฉาก (5 ม.) และด้านประชิด (3 ม.) เราจึงใช้ฟังก์ชันโคไซน์:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) ใช้เครื่องคิดเลขเพื่อหาค่าของ θ, \(\theta \approx 53.13^{\circ}\)
ตัวอย่างที่ 2: ประเมิน \(cos^{−1}(\frac{-1}{2}) \)
สารละลาย:
โดยใช้คุณสมบัติการสะท้อน: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
การแทนค่า \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
ตัวอย่างที่ 3: ประเมิน \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
สารละลาย:
โดยใช้เอกลักษณ์: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
ใน ฟังก์ชันตรีโกณมิติผกผัน โดเมน จะหมายถึงชุดค่าอินพุต (ค่า x) ที่ฟังก์ชันถูกกำหนด และ พิสัย จะหมายถึงชุดค่าเอาต์พุต (ค่า y) ที่ฟังก์ชันสามารถใช้ได้
ต่อไปนี้เป็นโดเมนและช่วงของฟังก์ชันตรีโกณมิติผกผันทั้งหก:
| ฟังก์ชัน | Domain | Range |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |