Ang anim na trigonometric function ay sin, cos, tan, cosec, sec at cot.
Subukan nating hanapin \(\angle A\) sa ibinigay na tatsulok.
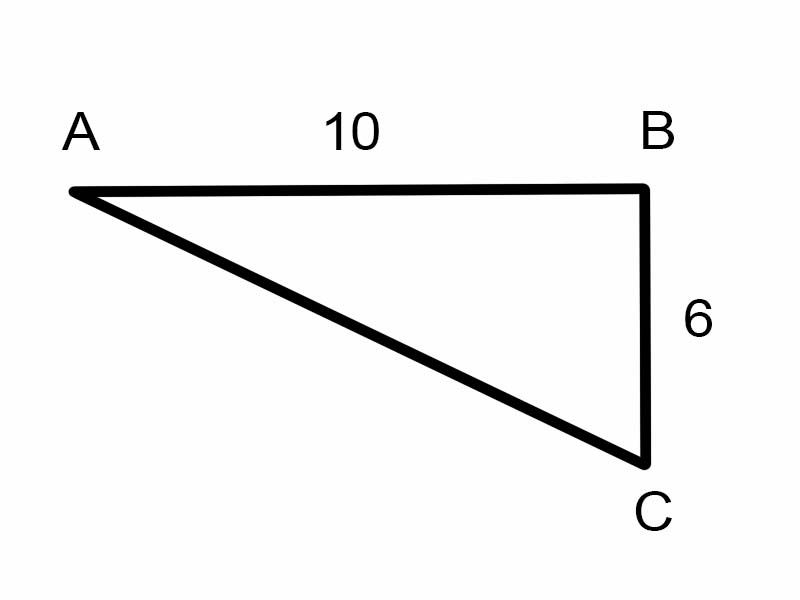
\(\tan A = \frac{6}{10}\)
Ngunit hindi ito nakakatulong upang mahanap ang sukat ng \(\angle A\)
Kailangan nating maghanap ng bagong kasangkapan sa matematika upang malutas ang mga problemang tulad nito. Ang mga function ng Sine, Cosine at Tangent ay kumukuha ng mga anggulo at nagbibigay ng mga side ratio. Ngunit kailangan namin ng mga function na kumukuha ng mga side ratio at nagbibigay ng mga anggulo at samakatuwid ay ipinakilala ang mga Inverse Trigonometric function .
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96° [Suriin gamit ang calculator]
Kung ang haba ng dalawang panig ay kilala, ang mga sukat ng anggulo ay maaaring matukoy gamit ang inverse trigonometric function.
\(\sin^{-1}x \textrm{ o } \arcsin x\) ay inverse sine function.
\(\cos^{-1}x \textrm{ o } \arccos x \) ay inverse cos function.
\(\tan^{-1}x \textrm{ o } \arctan x\) ay inverse tan function.
\(\csc^{-1}x \) o arccsc x ay inverse csc function.
\(\sec^{-1}x \) o arcsec x ay inverse sec function.
\(cot^{-1}x \) o arcot x ay inverse cot function.
Sa isang tatsulok, hayaan ang \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [bilang \(\sin\theta = \) Perpendicular∕ Hypotenuse]
Maaari tayong sumulat bilang \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Makukuha natin ang halaga ng trigonometric ratios kapag \(\theta\) ay ibinigay bilang kabaligtaran ayon sa talahanayan sa ibaba :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Halimbawa 1: Ang isang hagdan ay nakasandal sa isang pader, na gumagawa ng isang anggulo θ sa lupa. Ang base ng hagdan ay 3 metro ang layo mula sa dingding, at ang hagdan ay 5 metro ang haba. Hanapin ang θ.
Solusyon:
Dahil mayroon kaming hypotenuse (5 m) at ang katabing bahagi (3 m), ginagamit namin ang cosine function:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Gamitin ang calculator upang makuha ang halaga ng θ, \(\theta \approx 53.13^{\circ}\)
Halimbawa 2: Suriin ang \(cos^{−1}(\frac{-1}{2}) \)
Solusyon:
Gamit ang reflection property: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Pinapalitan ang \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Halimbawa 3: Suriin ang \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Solusyon:
Gamit ang pagkakakilanlan: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Sa inverse trigonometric functions , ang domain ay tumutukoy sa set ng input values (x-values) kung saan ang function ay tinukoy, at ang range ay tumutukoy sa set ng output values (y-values) na makukuha ng function.
Narito ang mga domain at hanay ng anim na kabaligtaran na trigonometric function:
| Saklaw ng | Domain | ng Pag-andar |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |