Altı trigonometrik fonksiyon sin, cos, tan, cosec, sec ve cot'tur.
Verilen üçgende \(\angle A\) bulmaya çalışalım.
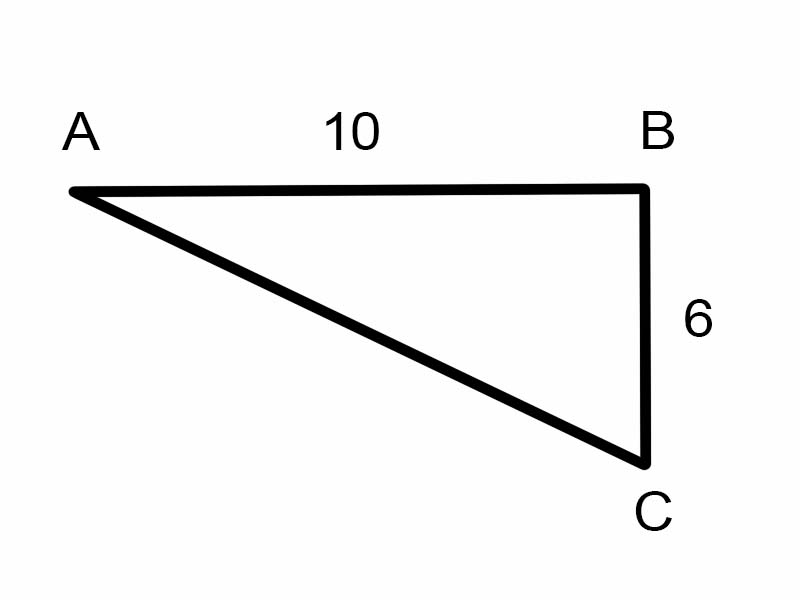
\(\tan A = \frac{6}{10}\)
Ancak bu \(\angle A\) ölçüsünü bulmak için yararlı değildir
Bu gibi problemleri çözmek için yeni bir matematiksel araç bulmamız gerekiyor. Sinüs, Kosinüs ve Tanjant fonksiyonları açıları alır ve kenar oranlarını verir. Ancak kenar oranlarını alan ve açıları veren fonksiyonlara ihtiyacımız var ve bu nedenle Ters Trigonometrik fonksiyonlar tanıtılıyor.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96° [Hesap makinesiyle değerlendirin]
İki kenar uzunluğu biliniyorsa, ters trigonometrik fonksiyon kullanılarak açı ölçüleri bulunabilir.
\(\sin^{-1}x \textrm{ veya } \arcsin x\) ters sinüs fonksiyonudur.
\(\cos^{-1}x \textrm{ veya } \arccos x \) ters cos fonksiyonudur.
\(\tan^{-1}x \textrm{ veya } \arctan x\) ters tan fonksiyonudur.
\(\csc^{-1}x \) veya arccsc x ters csc fonksiyonudur.
\(\sec^{-1}x \) veya arcsec x, ters sec fonksiyonudur.
\(cot^{-1}x \) veya arccot x ters cot fonksiyonudur.
Bir üçgende \(\sin \theta = x\) olsun
⇒ \(\sin \theta = {x \over 1}\) [ \(\sin\theta = \) Dik∕ Hipotenüs olarak]
\({x \over 1} = \frac{AB}{AC}\) şeklinde yazabiliriz
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Aşağıdaki tabloya göre \(\theta\) tersi verildiğinde trigonometrik oranların değerini elde edebiliriz :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Örnek 1: Bir merdiven bir duvara yaslanmış ve zeminle θ açısı yapıyor. Merdivenin tabanı duvardan 3 metre uzakta ve merdiven 5 metre uzunluğunda. θ'yi bulun.
Çözüm:
Hipotenüs (5 m) ve bitişik kenar (3 m) olduğundan kosinüs fonksiyonunu kullanırız:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) θ değerini türetmek için hesap makinesini kullanın, \(\theta \approx 53.13^{\circ}\)
Örnek 2: \(cos^{−1}(\frac{-1}{2}) \) değerini değerlendirin
Çözüm:
Yansıma özelliğini kullanarak: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\( x=\frac{1}{2} \) yerine koyma
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Örnek 3: \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \) değerini değerlendirin
Çözüm:
Kimliği kullanarak: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Ters trigonometrik fonksiyonlarda , tanım kümesi, fonksiyonun tanımlandığı girdi değerleri (x değerleri) kümesini, aralık ise fonksiyonun alabileceği çıktı değerleri (y değerleri) kümesini ifade eder.
Altı ters trigonometrik fonksiyonun tanım kümeleri ve değer kümeleri şunlardır:
| İşlev Etki | Alanı | Aralığı |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |