Шість тригонометричних функцій: sin, cos, tan, cosec, sec і cot.
Спробуємо знайти \(\angle A\) у даному трикутнику.
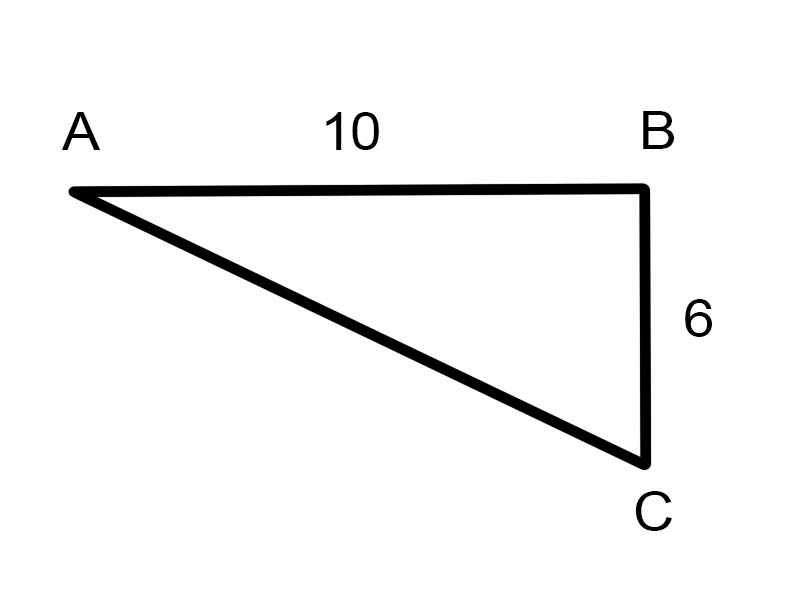
\(\tan A = \frac{6}{10}\)
Але це не допоможе знайти міру \(\angle A\)
Нам потрібно знайти новий математичний інструмент для вирішення подібних проблем. Функції синус, косинус і тангенс приймають кути та дають співвідношення сторін. Але нам потрібні функції, які приймають співвідношення сторін і дають кути, тому ми вводимо обернені тригонометричні функції .
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Вирахувати за допомогою калькулятора]
Якщо відомі довжини двох сторін, вимірювання кутів можна визначити за допомогою оберненої тригонометричної функції.
\(\sin^{-1}x \textrm{ або } \arcsin x\) є оберненою функцією.
\(\cos^{-1}x \textrm{ або } \arccos x \) є оберненою cos функцією.
\(\tan^{-1}x \textrm{ або } \arctan x\) — обернена функція tan.
\(\csc^{-1}x \) або arccsc x є оберненою функцією csc.
\(\sec^{-1}x \) або arcsec x є оберненою сек-функцією.
\(cot^{-1}x \) або arccot x — обернена функція cot.
Нехай у трикутнику \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [як \(\sin\theta = \) перпендикуляр∕ гіпотенуза]
Ми можемо записати як \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Ми можемо отримати значення тригонометричних співвідношень, коли \(\theta\) задано як обернене відповідно до таблиці нижче :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Приклад 1: Драбина спирається на стіну, утворюючи кут θ із землею. Основа драбини віддалена від стіни на 3 метри, а довжина драбини 5 метрів. Знайдіть θ.
рішення:
Оскільки у нас є гіпотенуза (5 м) і прилегла сторона (3 м), ми використовуємо функцію косинуса:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Використовуйте калькулятор, щоб отримати значення θ, \(\theta \approx 53.13^{\circ}\)
Приклад 2: обчисліть \(cos^{−1}(\frac{-1}{2}) \)
рішення:
Використання властивості відображення: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Підставляючи \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Приклад 3: обчисліть \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
рішення:
Використовуючи тотожність: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
В обернених тригонометричних функціях домен відноситься до набору вхідних значень (значення x), для яких визначено функцію, а діапазон відноситься до набору вихідних значень (значень y), які може приймати функція.
Ось області визначення та діапазони шести обернених тригонометричних функцій:
| Діапазон | домену | функції |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |