چھ مثلثی افعال گناہ، cos، tan، cosec، sec اور cot ہیں۔
آئیے دیے گئے مثلث میں \(\angle A\) تلاش کرنے کی کوشش کرتے ہیں۔
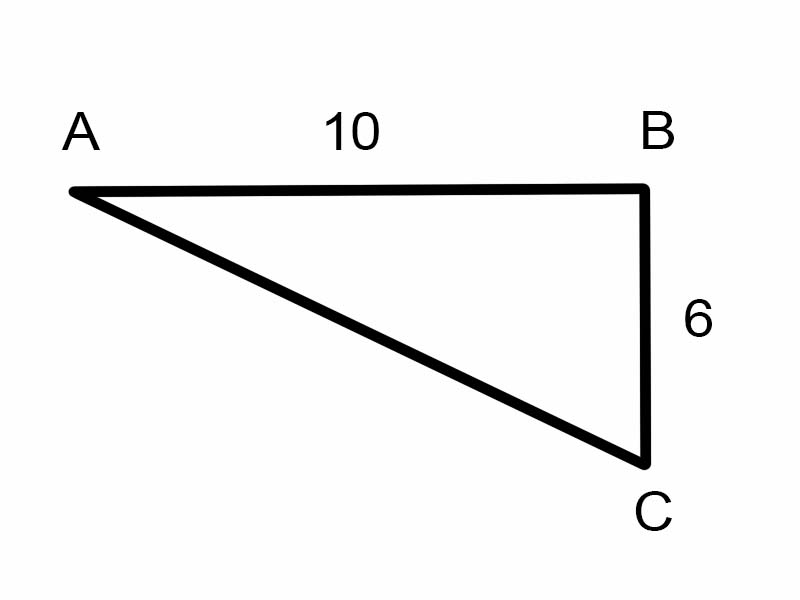
\(\tan A = \frac{6}{10}\)
لیکن یہ \(\angle A\) کی پیمائش تلاش کرنے میں مددگار نہیں ہے۔
ہمیں اس طرح کے مسائل کو حل کرنے کے لیے ایک نیا ریاضیاتی ٹول تلاش کرنے کی ضرورت ہے۔ سائن، کوزائن اور ٹینجنٹ فنکشن زاویہ لیتے ہیں اور ضمنی تناسب دیتے ہیں۔ لیکن ہمیں ایسے فنکشنز کی ضرورت ہے جو ضمنی تناسب لیں اور زاویہ دیں اور اسی وجہ سے الٹا ٹریگونومیٹرک فنکشنز متعارف کرائے گئے ہیں۔
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96° [کیلکولیٹر سے اندازہ کریں]
اگر دو اطراف کی لمبائی معلوم ہو تو، الٹا مثلثی فعل کا استعمال کرتے ہوئے زاویہ کی پیمائش کا تعین کیا جا سکتا ہے۔
\(\sin^{-1}x \textrm{ یا } \arcsin x\) الٹا سائن فنکشن ہے۔
\(\cos^{-1}x \textrm{ یا } \arccos x \) الٹا cos فعل ہے۔
\(\tan^{-1}x \textrm{ یا } \arctan x\) الٹا ٹین فنکشن ہے۔
\(\csc^{-1}x \) یا arccsc x الٹا csc فنکشن ہے۔
\(\sec^{-1}x \) یا arcsec x الٹا سیکنڈ فنکشن ہے۔
\(cot^{-1}x \) یا arccot x الٹا cot فعل ہے۔
ایک مثلث میں چلو \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [جیسے \(\sin\theta = \) Perpendicular∕ Hypotenuse]
ہم بطور \({x \over 1} = \frac{AB}{AC}\) لکھ سکتے ہیں۔
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
ہم مثلثی تناسب کی قدر حاصل کر سکتے ہیں جب \(\theta\) نیچے دیے گئے جدول کے مطابق الٹا دیا جائے :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
مثال 1: ایک سیڑھی دیوار سے ٹیک لگا کر زمین کے ساتھ θ زاویہ بناتی ہے۔ سیڑھی کی بنیاد دیوار سے 3 میٹر کے فاصلے پر ہے، اور سیڑھی 5 میٹر لمبی ہے۔ θ تلاش کریں۔
حل:
چونکہ ہمارے پاس hypotenuse (5m) اور ملحقہ سائیڈ (3m) ہے، ہم کوسائن فنکشن استعمال کرتے ہیں:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) θ کی قدر حاصل کرنے کے لیے کیلکولیٹر استعمال کریں، \(\theta \approx 53.13^{\circ}\)
مثال 2: اندازہ کریں \(cos^{−1}(\frac{-1}{2}) \)
حل:
عکاسی کی خاصیت کا استعمال کرتے ہوئے: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
متبادل \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
مثال 3: اندازہ کریں \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
حل:
شناخت کا استعمال کرتے ہوئے: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
الٹا ٹرگنومیٹرک فنکشنز میں، ڈومین ان پٹ ویلیوز (x-values) کے سیٹ سے مراد ہے جس کے لیے فنکشن کی وضاحت کی گئی ہے، اور رینج سے مراد آؤٹ پٹ ویلیوز (y-values) کا وہ سیٹ ہے جو فنکشن لے سکتا ہے۔
چھ الٹا مثلثی افعال کے ڈومینز اور رینجز یہ ہیں:
| فنکشن | ڈومین | رینج |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |