Oltita trigonometrik funksiyalar sin, kos, tan, kosek, sek va kot.
Keling, berilgan uchburchakda \(\angle A\) topishga harakat qilaylik.
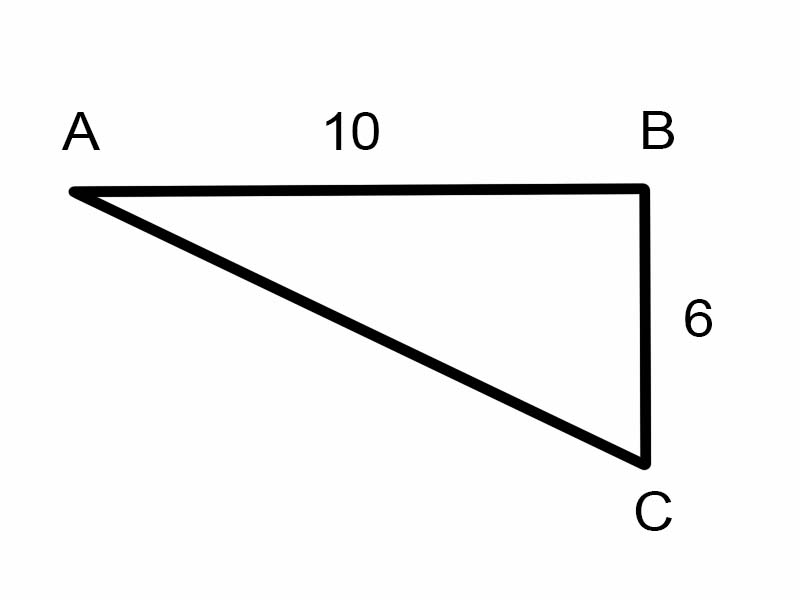
\(\tan A = \frac{6}{10}\)
Ammo bu \(\angle A\) o'lchovini topish uchun foydali emas.
Bu kabi muammolarni hal qilish uchun yangi matematik vositani topishimiz kerak. Sinus, kosinus va tangens funksiyalari burchaklarni oladi va yon nisbatlarini beradi. Lekin bizga yon nisbatlarni oladigan va burchaklarni beradigan funksiyalar kerak va shuning uchun Teskari trigonometrik funksiyalar kiritiladi.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Kalkulyator bilan baholang]
Ikki tomonning uzunligi ma'lum bo'lsa, burchak o'lchovlarini teskari trigonometrik funktsiya yordamida aniqlash mumkin.
\(\sin^{-1}x \textrm{ yoki } \arcsin x\) teskari sinus funksiyasi.
\(\cos^{-1}x \textrm{ yoki } \arccos x \) teskari cos funksiyasi.
\(\tan^{-1}x \textrm{ yoki } \arctan x\) teskari tan funksiyasi.
\(\csc^{-1}x \) yoki arccsc x teskari csc funksiyasi.
\(\sec^{-1}x \) yoki arcsec x teskari soniya funksiyasi.
\(cot^{-1}x \) yoki arccot x - teskari karyola funktsiyasi.
Uchburchakda \(\sin \theta = x\) bo'lsin.
⇒ \(\sin \theta = {x \over 1}\) [ \(\sin\theta = \) Perpendikulyar∕ Gipotenuza]
Biz shunday yozishimiz mumkin: \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Quyidagi jadvalga muvofiq \(\theta\) teskari berilganda trigonometrik nisbatlarning qiymatini olishimiz mumkin :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
1-misol: Narvon devorga suyanib, yer bilan th burchak hosil qiladi. Narvonning poydevori devordan 3 metr uzoqlikda, narvonning uzunligi esa 5 metrni tashkil qiladi. th ni toping.
Yechim:
Bizda gipotenuza (5 m) va qo'shni tomon (3 m) bo'lgani uchun biz kosinus funktsiyasidan foydalanamiz:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) th qiymatini chiqarish uchun kalkulyatordan foydalaning, \(\theta \approx 53.13^{\circ}\)
2-misol: \(cos^{−1}(\frac{-1}{2}) \) ni baholang
Yechim:
Ko'zgu xususiyatidan foydalanish: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\( x=\frac{1}{2} \) almashtirilmoqda
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
3-misol: \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \) ni baholang
Yechim:
Identifikatsiyadan foydalanish: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Teskari trigonometrik funktsiyalarda domen funktsiya belgilangan kirish qiymatlari (x-qiymatlari) to'plamiga, diapazon esa funktsiya qabul qilishi mumkin bo'lgan chiqish qiymatlari to'plamiga (y-qiymatlari) ishora qiladi.
Mana oltita teskari trigonometrik funksiyalarning domenlari va diapazonlari:
| Funktsiyaning | domen | diapazoni |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) = |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |