Sáu hàm lượng giác là sin, cos, tan, cosec, sec và cot.
Chúng ta hãy thử tìm \(\angle A\) trong tam giác cho sẵn.
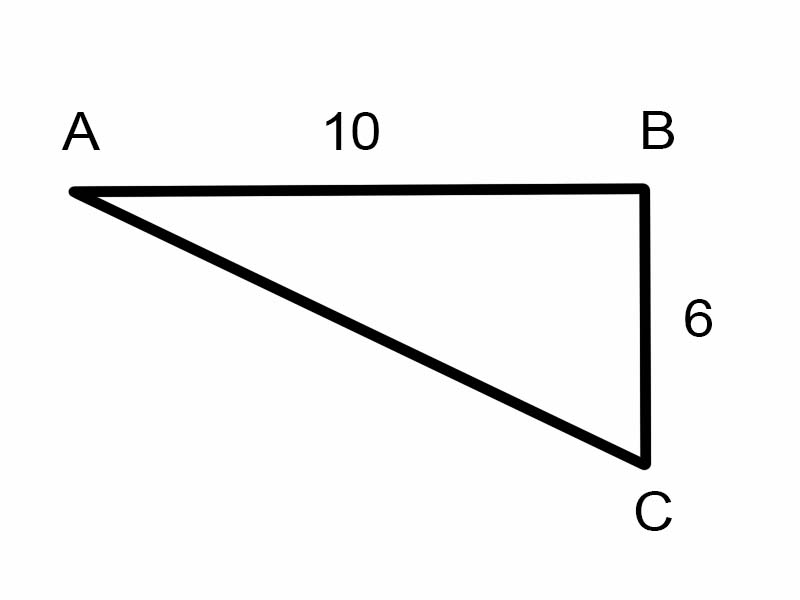
\(\tan A = \frac{6}{10}\)
Nhưng điều này không hữu ích để tìm số đo của \(\angle A\)
Chúng ta cần tìm một công cụ toán học mới để giải các bài toán như thế này. Các hàm Sine, Cosine và Tangent lấy các góc và đưa ra các tỷ số cạnh. Nhưng chúng ta cần các hàm lấy các tỷ số cạnh và đưa ra các góc và do đó các hàm lượng giác ngược được giới thiệu.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Đánh giá bằng máy tính]
Nếu biết độ dài của hai cạnh, số đo góc có thể được xác định bằng hàm lượng giác nghịch đảo.
\(\sin^{-1}x \textrm{ hoặc } \arcsin x\) là hàm sin nghịch đảo.
\(\cos^{-1}x \textrm{ hoặc } \arccos x \) là hàm cos nghịch đảo.
\(\tan^{-1}x \textrm{ hoặc } \arctan x\) là hàm tan nghịch đảo.
\(\csc^{-1}x \) hoặc arccsc x là hàm csc nghịch đảo.
\(\sec^{-1}x \) hay arcsec x là hàm nghịch đảo của sec.
\(cot^{-1}x \) hoặc arccot x là hàm cot nghịch đảo.
Trong một tam giác, hãy cho \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [khi \(\sin\theta = \) Vuông góc∕ Cạnh huyền]
Chúng ta có thể viết như \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Chúng ta có thể suy ra giá trị của tỉ số lượng giác khi \(\theta\) được đưa ra dưới dạng nghịch đảo theo bảng dưới đây :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Ví dụ 1: Một cái thang dựa vào tường, tạo với mặt đất một góc θ. Chân thang cách tường 3 mét, và thang dài 5 mét. Tìm θ.
Giải pháp:
Vì ta có cạnh huyền (5 m) và cạnh kề (3 m), ta sử dụng hàm cosin:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Sử dụng máy tính để tính giá trị của θ, \(\theta \approx 53.13^{\circ}\)
Ví dụ 2: Đánh giá \(cos^{−1}(\frac{-1}{2}) \)
Giải pháp:
Sử dụng tính chất phản xạ: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Thay thế \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Ví dụ 3: Tính \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Giải pháp:
Sử dụng hằng đẳng thức: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Trong các hàm lượng giác nghịch đảo , miền xác định là tập hợp các giá trị đầu vào (giá trị x) mà hàm được xác định, còn phạm vi xác định là tập hợp các giá trị đầu ra (giá trị y) mà hàm có thể nhận.
Sau đây là miền xác định và tập giá trị của sáu hàm lượng giác nghịch đảo:
| Phạm | vi miền | hàm |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |