راقب الأشياء المختلفة من حولك. يأتون بأشكال وأحجام مختلفة. بعضها متشابه وبعضها مختلف. على الرغم من أننا لا نستطيع تحديد أشكال جميع الكائنات بدقة ، إلا أننا في الرياضيات نتحدث إلى حد كبير عن الأشكال ثنائية الأبعاد والأشكال ثلاثية الأبعاد. دعونا نتعلم المزيد عنهم!
تشير كلمة شكل ثنائي الأبعاد إلى شكل "ثنائي الأبعاد". الشكل الهندسي ذو البعدين - الطول والعرض فقط هو شكل ثنائي الأبعاد. الأشكال ثنائية الأبعاد ليس لها سمك. الجوانب مصنوعة من خطوط مستقيمة أو منحنية. يمكن أن يكون لديهم أي عدد من الجوانب.
يمكن اعتبار مفهوم البعدين على أنه سطح مستوٍ يستطيع المرء أن يتحرك عليه في أي مكان. يُعرف السطح المسطح بالطائرة. الشكل ثنائي الأبعاد هو شيء يقع دائمًا على ورقة. ليس لها ارتفاع ، وبالتالي فهي لا تقع فوق قطعة الورق. تُعرف الأشكال ثنائية الأبعاد أيضًا بأشكال الطائرة أو الأشكال المستوية.
الأشكال ثنائية الأبعاد لها مساحة ولكن ليس لها حجم.
هناك ثلاث مصطلحات مهمة لتحديد خصائص الأشكال:
الجوانب - قطعة مستقيمة تشكل شكلاً على شكل ثنائي الأبعاد.
الرؤوس - زاوية الشكل.
الزوايا - في الهندسة ، يمكن تعريف الزاوية على أنها شكل يتكون من خطين يلتقيان عند نقطة نهاية مشتركة.
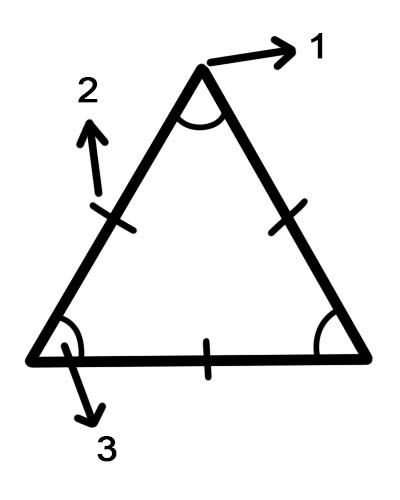
1. قمة الرأس
2. الجوانب
3. الزوايا
دعونا نناقش الأشكال ثنائية الأبعاد المختلفة.

الدائرة عبارة عن شكل دائري ليس له زوايا أو حواف. يمكننا أن نجد شكل دائرة في إطار سيارة وساعة حائط ومصاصة من حولنا. مركز الدائرة هو النقطة المركزية في الدائرة ، والتي من خلالها تتساوى جميع المسافات إلى النقاط الموجودة على الدائرة. المسافة من المركز إلى أي نقطة في الدائرة تسمى نصف القطر. إذا اعتبرنا المسافة عبر الدائرة ، التي تمر عبر المركز ، فهذا هو القطر. تسمى المسافة حول الدائرة محيط الدائرة.
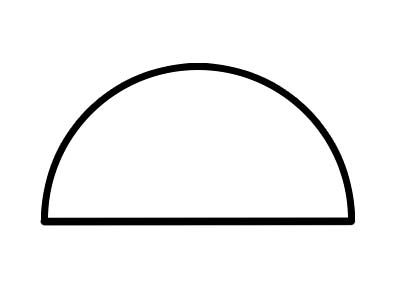
نصف الدائرة هو نصف دائرة ، يتكون من قطع دائرة كاملة على طول خط قطر ، كما هو موضح أعلاه. أي قطر دائرة يقطعها إلى نصفين متساويين. دائمًا ما يقيس القوس الكامل لنصف الدائرة 180 درجة. إذا تم تقطيع ملف تعريف الارتباط إلى نصفين ، فسيكون كل نصف نصف دائرة.

البيضاوي لها شكل أو شكل أو مخطط تفصيلي للبيضة. ليس للشكل البيضاوي جوانب مستقيمة ولا زوايا ، لكن له وجه واحد يمكن تتبعه أو رؤيته كشكل مسطح عند النظر إليه.
المضلع شكل مستو بخطوط مستقيمة. تشمل الأمثلة المثلثات والأشكال الرباعية والخماسية والأشكال السداسية وما إلى ذلك. المضلع المنتظم جميع أضلاعه متساوية وجميع الزوايا متساوية. خلاف ذلك ، يكون مضلع غير منتظم.
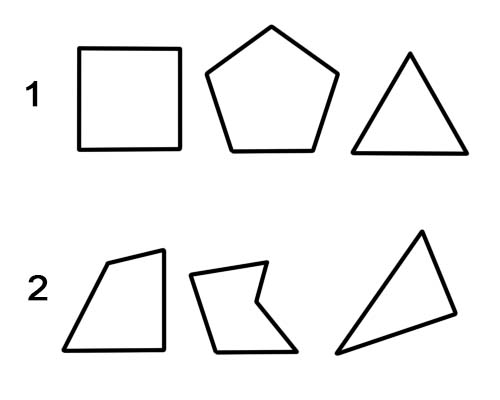
1. مضلع منتظم.
2. مضلع غير منتظم.
الدوائر والأشكال التي تتضمن منحنيات ليست مضلعات - فالمضلع ، بحكم التعريف ، يتكون من خطوط مستقيمة.

في الهندسة ، المثلث هو شكل مغلق ثنائي الأبعاد بثلاثة خطوط مستقيمة. المثلث هو أيضًا مضلع.
يمكننا أن نجد شكل المثلث في العلم ولافتة على جانب الطريق وشطيرة.
المثلث له ثلاثة أضلاع وثلاثة رؤوس وثلاث زوايا.
مجموع الزوايا الداخلية الثلاث للمثلث يساوي دائمًا 180 درجة. دائمًا ما يكون مجموع طول ضلعي المثلث أكبر من طول الضلع الثالث.
لتصنيف المثلثات وفقًا لزواياها ، نقيس كل زاوية من زواياها الداخلية. يمكن تصنيف المثلثات حسب الزوايا ، على النحو التالي:
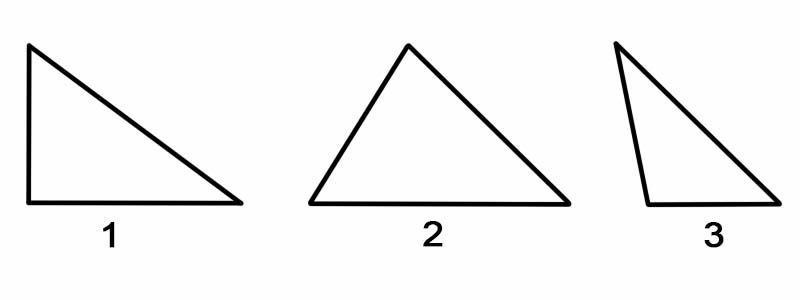
لتصنيف المثلثات وفقًا لأضلاعها ، نقيس طول كل جانب منها. يمكن تصنيف المثلثات حسب جوانبها على النحو التالي:
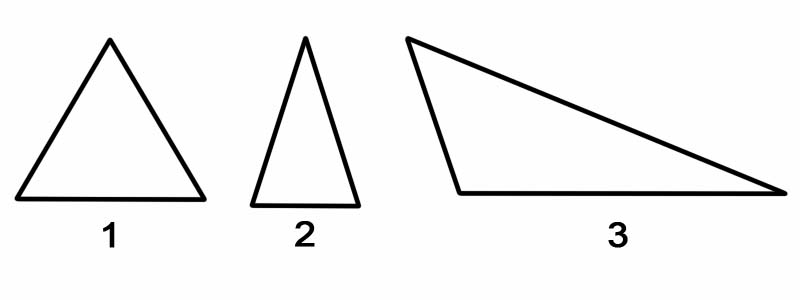
تذكر: يمكن دائمًا تقسيم المثلث إلى مثلثين قائم الزاوية ، بغض النظر عن اتجاهه.
المثلثات هي مضلعات لها أقل عدد من الأضلاع.
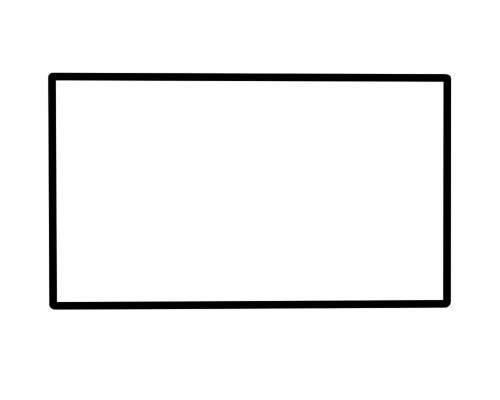
المستطيل عبارة عن شكل به 4 جوانب و 4 رؤوس و 4 زوايا. الأضلاع المتقابلة متوازية ومتساوية في الطول. قياس الزوايا الأربع 90 درجة.
تبدو الجداول والصناديق والكتب والأبواب والورق مثل المستطيلات.

المعين هو شكل مكون من 4 خطوط مستقيمة. تقيس أضلاعه الأربعة نفس الطول ، ولكن على عكس المستطيل ، لا يقيس أي من الزوايا الأربع 90 درجة. يشبه المعين الماس. الأضلاع المتقابلة متوازية والزوايا المتقابلة متساوية. قطري المعين متعامدين مع بعضهما البعض.

المربع عبارة عن شكل ثنائي الأبعاد حيث تكون الأضلاع الأربعة متساوية الطول والضلعان المتقابلان متوازيان. إنه نوع من المستطيل والمعين (تمت مناقشته أدناه). الزوايا الأربع الداخلية للمربع هي 90 درجة ، أو بعبارة أخرى ، إنها زوايا قائمة. عند جمع كل الزوايا معًا ، فإن مجموعها يصل إلى 360 درجة. القطران اللذان لهما مربع متساويان في الطول والنقطة التي يتقاطعان فيها هي مركز المربع.
تذكر: المربع دائمًا ما يكون معينًا ولكن المعين ليس دائمًا مربعًا. إذا كانت كل زاوية في المعين تساوي 90 درجة ، فهذا يعني أنها مربع.
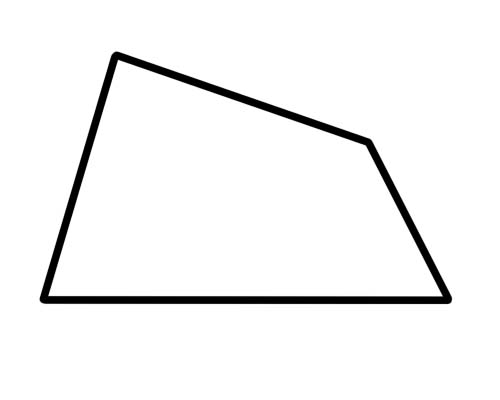
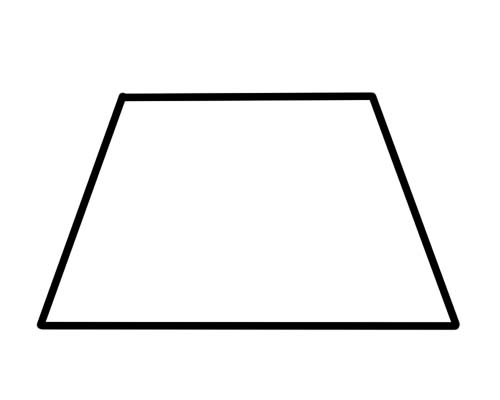
شبه المنحرف هو شكل رباعي متوازي ضلعين فقط.
هذا هو. لا حاجة لأن تكون الأضلاع متطابقة (أو متساوية) ولا حاجة لأن تكون الزوايا متطابقة. لا شيء مميز يحدث مع الأقطار. نوع خاص من شبه المنحرف هو "شبه منحرف متساوي الساقين" الذي له جوانب متقابلة من نفس الطول وزوايا متقابلة لنفس المقياس. الأقطار متساوية الطول أيضًا.
في المثلث متساوي الساقين ، تكون الزوايا المتجاورة على طول الجوانب (الزوايا المجاورة لبعضها البعض) مكملة. هذا يعني أنها تضيف ما يصل إلى 180 درجة.
إن شبه المنحرف ليس متوازي أضلاع لأن زوجًا واحدًا فقط من الأضلاع المتقابلة متوازي.
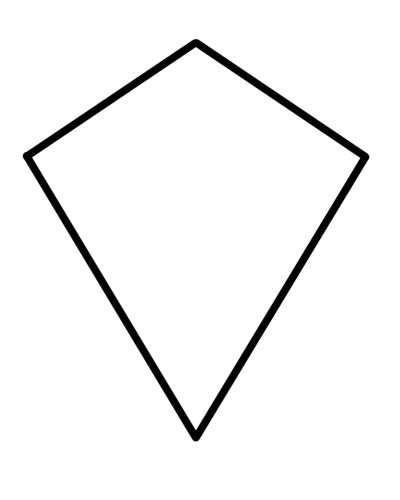
الطائرة الورقية هي شكل رباعي الأضلاع به زوجان بالضبط من الضلع المتتالي المتساوي أو يكون فيه زوجان منفصلان من الأضلاع المتتالية متطابقتين (الأزواج المنفصلة تعني أنه لا يمكن استخدام جانب واحد في كلا الزوجين).
عليك أن تعرف أن كل معين هو طائرة ورقية ، لأن المعين يلبي جميع خصائص الطائرة الورقية. تصبح الطائرة الورقية ذات الجوانب المتقابلة متوازية بالتأكيد معينًا. وبالتالي فإن كل المعين هو طائرة ورقية ولكن ليس العكس. الطائرة الورقية ليست متوازي أضلاع لأن الأضلاع المتقابلة ليست موازية لبعضها البعض.
الأشكال الرباعية - يسمى الشكل الرباعي الشكل الرباعي
متوازي الأضلاع - متوازي الأضلاع هو شكل مسطح أضلاعه متقابلة متوازية ومتساوية في الطول.
وهكذا ، فإن أشكال المستطيل والمربع والمعين والربعيزيوم والطائرة الورقية هي أشكال رباعية الأضلاع لأن لكل منها أربعة جوانب.
ومع ذلك ، فإن المستطيل والمربع والمعين فقط هي متوازيات الأضلاع.
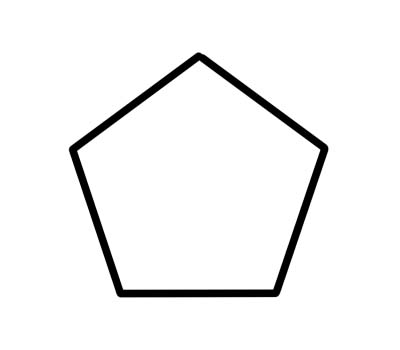
البنتاغون عبارة عن مضلع خماسي الأضلاع بخمس زوايا داخلية تضيف 540 درجة. الخماسي المنتظم له أضلاع متساوية الطول وكل زاوية داخلية 108 درجة.
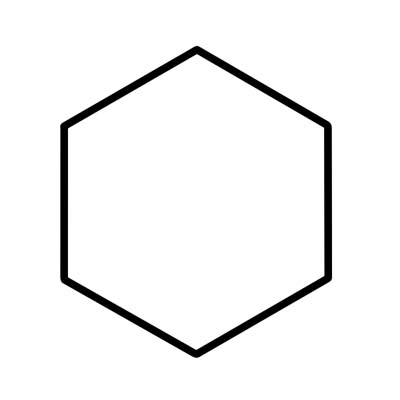
السداسي هو مضلع سداسي الأضلاع له ست زوايا داخلية مجموعها 720 درجة. السداسي غير المنتظم له جوانب مختلفة الطول.
السداسي المنتظم له أضلاع متساوية الطول وكل زاوية داخلية 120 درجة. يتكون الشكل السداسي المنتظم من ستة مثلثات متساوية الأضلاع كل زاوية مركزية فيها تساوي 60 درجة.
[أدخل الصورة: مسدس مقسم إلى ستة مثلثات وزاوية مركزية واحدة قياسها 60 درجة]
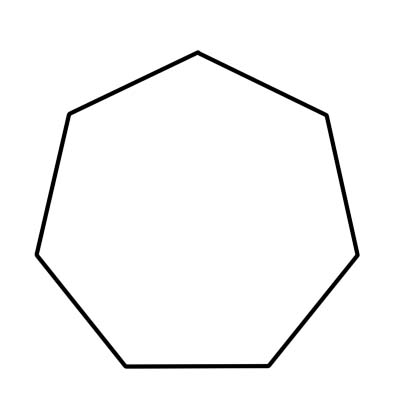
سباعي الأضلاع هو مضلع بسبعة أضلاع. إلى جانب سبعة أضلاع ، يحتوي الشكل سباعي الأضلاع على سبعة رءوس وزوايا. مجموع الزوايا السبع الداخلية مجموعها 900 درجة. قياس كل زاوية داخلية لسباعي منتظم حوالي 128.57 درجة أو ما يقرب من 129 درجة.
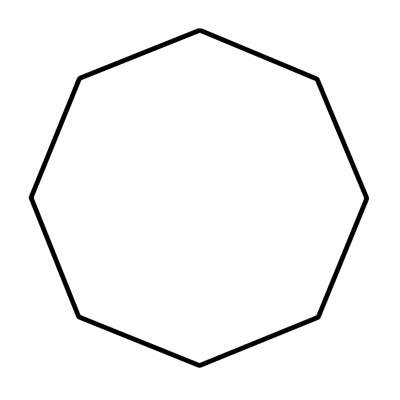
المثمن هو شكل هندسي يحتوي على ثمانية جوانب وثماني زوايا. يجب أن يكون للمثمنات جوانب مستقيمة متصلة ؛ لا يمكن أن تكون منحنية أو منفصلة. سترى غالبًا مثمنات في الحياة الواقعية على شكل علامة توقف. قياس كل زاوية من الزوايا الداخلية الثمانية لشكل ثماني منتظم يساوي 108 درجات تقريبًا. المثمن المحدب ليس له زوايا تشير إلى الداخل. بتعبير أدق ، لا يمكن أن تزيد الزوايا الداخلية عن 180 درجة. عندما تكون أي زاوية داخلية أكبر من 180 درجة فإنها تكون مقعرة
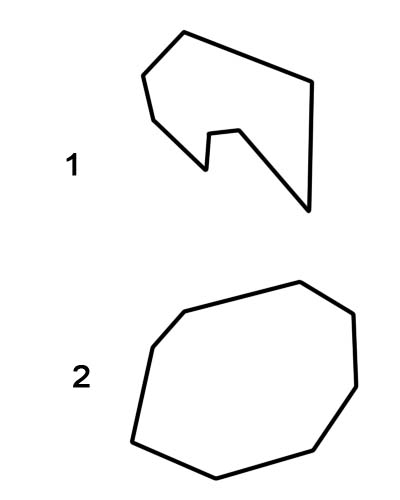
1. مثمن مقعر
2. مثمن محدب
من المهم أن نلاحظ أن المثمنات العادية تصنف دائمًا على أنها مثمنة محدبة ، في حين أن المثمنات غير المنتظمة يمكن أن تكون مقعرة أو محدبة.
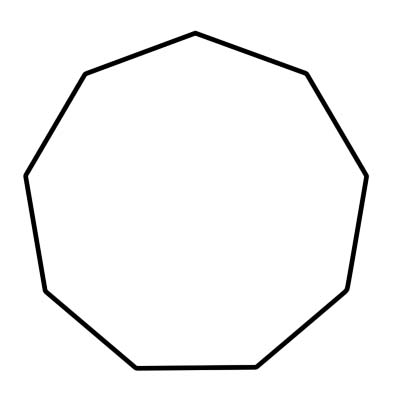
المضلع غير المضلع هو مضلع به 9 جوانب و 9 زوايا داخلية مجموعها 1260 درجة. الأضلاع العادية لها نفس الطول وجميع الزوايا الداخلية لها نفس الحجم. قياس زاوية نوناجون منتظم 140 درجة. يتكون غير المضلع من 9 مثلثات مع قياس كل زاوية مركزية 40 درجة.
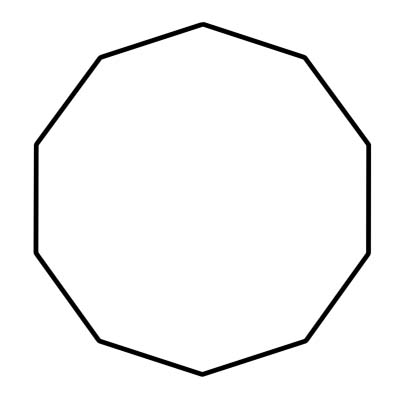
العشاري هو مضلع ذو 10 أضلاع. كما أن لديها عشرة رؤوس - حيث تلتقي الأضلاع - وزوايا. مجموع الزوايا الداخلية لعشر أضلاع يساوي 1440 درجة. عشري منتظم له جوانب وزوايا متطابقة. قياس كل زاوية 144 درجة. يتكون عشري الأضلاع من 10 مثلثات بزاوية مركزية تساوي 36 درجة.
تسمى الأشكال التي يمكن قياسها في ثلاثة اتجاهات الأشكال ثلاثية الأبعاد أو الأشكال ثلاثية الأبعاد. تسمى الأشكال ثلاثية الأبعاد أيضًا الأشكال الصلبة. القياسات الثلاثة للأشكال ثلاثية الأبعاد هي - الطول والعرض والارتفاع (أو العمق أو السماكة).
تختلف الأشكال ثلاثية الأبعاد عن الأشكال ثنائية الأبعاد نظرًا لسمكها. بعض الأمثلة على الأشكال ثلاثية الأبعاد من حياتنا اليومية هي:
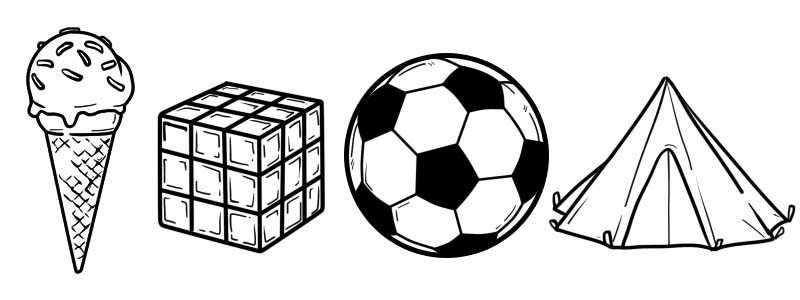
الأشكال ثلاثية الأبعاد لها رؤوس ووجوه وحواف.
المنشور هو نوع من الأشكال ثلاثية الأبعاد ذات جوانب مسطحة. له طرفان لهما نفس الشكل والحجم (ويبدو أنهما شكل ثنائي الأبعاد). لها نفس المقطع العرضي مع الشكل من النهاية إلى النهاية ؛ هذا يعني أنه إذا قمت بقصها ، فسترى نفس الشكل ثنائي الأبعاد الموجود على كلا الجانبين.
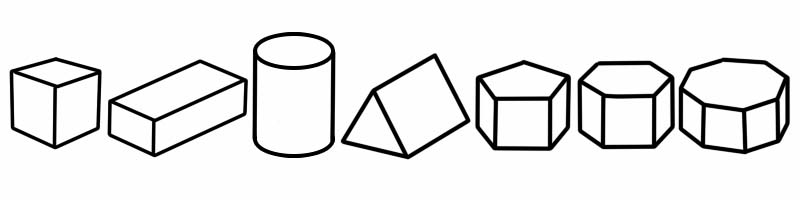
شكل ثلاثي الأبعاد | عدد الحواف | عدد الوجوه | عدد الرؤوس |
مكعب | 12 | 6 | 8 |
مكعباني شبيه بالمكعب | 12 | 6 | 8 |
اسطوانة | 2 | 3 | 0 |
منشور ثلاثي | 9 | 5 (2 مثلثات ، 3 مستطيلات) | 6 |
منشور خماسي | 15 | 7 | 10 |
منشور سداسي | 18 | 8 | 12 |
منشور مثمن | 24 | 10 | 16 |
الهرم هو أيضًا شكل ثلاثي الأبعاد. لها قاعدة مضلعة وجوانب مسطحة (مثلثة) تلتقي عند نقطة مشتركة (تسمى القمة). عندما يتم ذكر كلمة "هرم" ، فإن أول ما يتبادر إلى أذهاننا هو أهرامات مصر الشهيرة. الأهرامات المصرية هي أهرامات مربعة الشكل ، ولكن هناك عدة أنواع أخرى من الأهرامات ، ولكل منها مضلع مختلف كقاعدة لها.
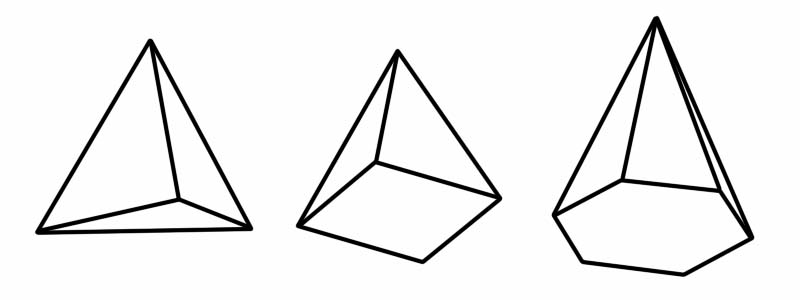
شكل | عدد الحواف | عدد الوجوه | عدد الرؤوس |
رباعي الوجوه | 6 | 4 | 4 |
هرم مربع | 8 | 5 | 5 |
هرم سداسي | 12 | 7 | 7 |
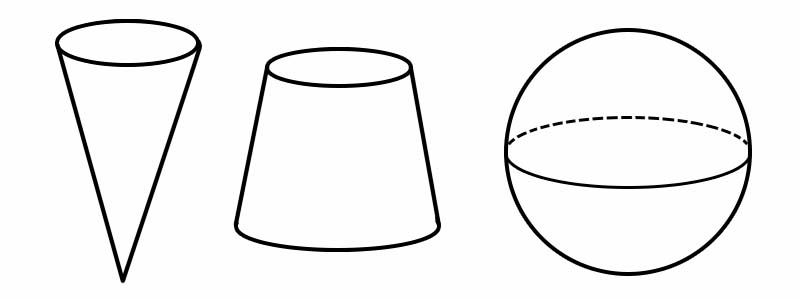
شكل | عدد الحواف | عدد الوجوه | عدد الرؤوس |
مخروط | 1 | 2 | 1 |
فروستم | 2 | 3 | 0 |
جسم كروى | 0 | 1 | 0 |