আপনার চারপাশের বিভিন্ন বস্তু পর্যবেক্ষণ করুন। তারা বিভিন্ন আকার এবং আকারে আসে। কিছু একই এবং কিছু ভিন্ন। যদিও আমরা সব বস্তুর আকারের সঠিক নাম বলতে পারি না, গণিতে আমরা মূলত 2D আকার এবং 3D আকারের কথা বলি। আসুন তাদের সম্পর্কে আরও জানুন!
2D আকৃতি শব্দটি একটি "দ্বিমাত্রিক" আকৃতি বোঝায়। একটি জ্যামিতিক চিত্র যার দুটি মাত্রা আছে - দৈর্ঘ্য এবং প্রস্থ শুধুমাত্র একটি 2D আকৃতি। দ্বিমাত্রিক আকৃতির কোন বেধ নেই। পাশগুলো সোজা বা বাঁকা রেখা দিয়ে তৈরি। তাদের যেকোনো দিক থাকতে পারে।
দুটি মাত্রার ধারণাটি একটি সমতল পৃষ্ঠ হিসাবে চিন্তা করা যেতে পারে যার উপর কেউ যে কোনও জায়গায় যেতে সক্ষম। সমতল পৃষ্ঠ একটি সমতল হিসাবে পরিচিত। একটি 2D আকৃতি এমন একটি জিনিস যা সবসময় কাগজের পাতায় থাকে। এর কোন উচ্চতা নেই, এবং তাই এটি কাগজের টুকরোর উপরে পড়ে না। 2 ডি আকারগুলি প্লেন শেপ বা প্লেন ফিগার নামেও পরিচিত।
2D আকারের ক্ষেত্র আছে কিন্তু আয়তন নেই।
আকৃতির বৈশিষ্ট্যগুলি রূপরেখা করার জন্য তিনটি গুরুত্বপূর্ণ পদ রয়েছে:
সাইডস - একটি লাইন সেগমেন্ট যা একটি দ্বিমাত্রিক চিত্রে আকৃতি তৈরি করে।
শিরোনাম - একটি চিত্রের একটি কোণ।
কোণ - জ্যামিতিতে, একটি কোণকে একটি সাধারণ প্রান্তবিন্দুতে মিলিত দুটি লাইন দ্বারা গঠিত চিত্র হিসাবে সংজ্ঞায়িত করা যেতে পারে।
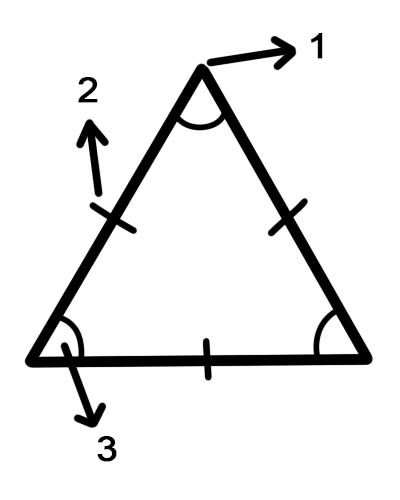
1. শিরোনাম
2. পক্ষ
3. কোণ
আসুন বিভিন্ন 2D আকার নিয়ে আলোচনা করি।

বৃত্ত হল বৃত্তাকার আকৃতির চিত্র যার কোন কোণ বা প্রান্ত নেই। আমরা আমাদের চারপাশে একটি গাড়ির টায়ার, প্রাচীর ঘড়ি এবং একটি ললিপপ একটি বৃত্তের আকৃতি খুঁজে পেতে পারি। একটি বৃত্তের কেন্দ্র হল একটি বৃত্তের কেন্দ্র বিন্দু, যেখান থেকে বৃত্তের বিন্দুর সমস্ত দূরত্ব সমান। কেন্দ্র থেকে বৃত্তের যেকোনো বিন্দুর দূরত্বকে ব্যাসার্ধ বলে। যদি আমরা বৃত্ত জুড়ে দূরত্ব বিবেচনা করি, কেন্দ্রের মধ্য দিয়ে যাচ্ছি, এটি ব্যাস। বৃত্তের চারপাশের দূরত্বকে বৃত্তের পরিধি বলে।
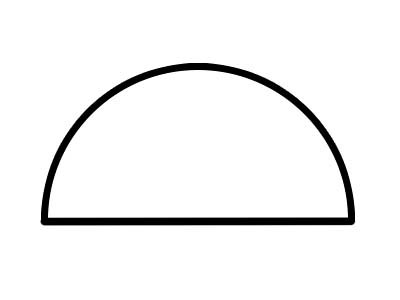
একটি অর্ধবৃত্ত হল একটি অর্ধবৃত্ত, যা একটি ব্যাস রেখা বরাবর একটি সম্পূর্ণ বৃত্ত কেটে কেটে তৈরি করা হয়েছে, যেমনটি উপরে দেখানো হয়েছে। বৃত্তের যেকোন ব্যাস এটিকে দুটি সমান অর্ধবৃত্তে বিভক্ত করে। একটি অর্ধবৃত্তের পূর্ণ চাপ সবসময় 180 measures পরিমাপ করে। যদি একটি কুকি দুই ভাগে কাটা হয়, তাহলে প্রতিটি অর্ধেক একটি অর্ধবৃত্ত।

একটি ডিম্বাকৃতির ডিমের আকার, আকৃতি বা রূপরেখা থাকে। একটি ডিম্বাকৃতির কোন সোজা দিক নেই এবং কোন কোণ নেই, কিন্তু এর 1 টি মুখ রয়েছে, যা এটির দিকে তাকালে সমতল আকৃতি হিসাবে চিহ্নিত করা যায় বা দেখা যায়।
বহুভুজ হল সরলরেখার সমতল আকৃতি। উদাহরণগুলির মধ্যে রয়েছে ত্রিভুজ, চতুর্ভুজ, পেন্টাগন, ষড়ভুজ ইত্যাদি। একটি নিয়মিত বহুভুজের সব বাহু সমান এবং সব কোণ সমান। অন্যথায়, এটি একটি অনিয়মিত বহুভুজ।
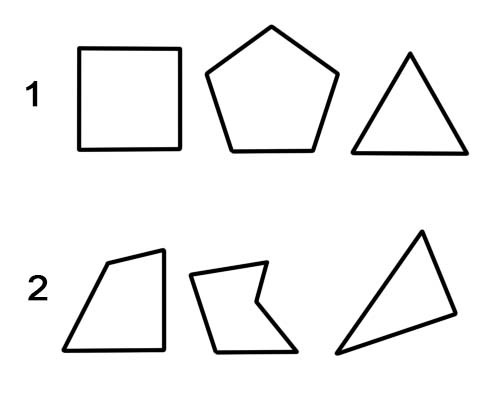
1. নিয়মিত বহুভুজ।
2. অনিয়মিত বহুভুজ।
বৃত্ত এবং আকৃতি যার মধ্যে কার্ভ অন্তর্ভুক্ত বহুভুজ নয় - একটি বহুভুজ, সংজ্ঞা অনুসারে, সরলরেখা দ্বারা গঠিত।

জ্যামিতিতে, একটি ত্রিভুজ হল একটি বদ্ধ, দ্বিমাত্রিক আকৃতি যার তিনটি সরলরেখা রয়েছে। ত্রিভুজটিও বহুভুজ।
আমরা একটি পতাকা, একটি রাস্তার পাশে সাইনবোর্ড এবং একটি স্যান্ডউইচে একটি ত্রিভুজের আকৃতি খুঁজে পেতে পারি।
একটি ত্রিভুজের তিনটি বাহু, তিনটি কোণ এবং তিনটি কোণ রয়েছে।
একটি ত্রিভুজের তিনটি অভ্যন্তরীণ কোণের সমষ্টি সর্বদা 180। ত্রিভুজের দুই বাহুর দৈর্ঘ্যের যোগফল সর্বদা তৃতীয় বাহুর দৈর্ঘ্যের চেয়ে বেশি।
ত্রিভুজগুলিকে তাদের কোণ অনুসারে শ্রেণিবদ্ধ করার জন্য, আমরা এর প্রতিটি অভ্যন্তরীণ কোণ পরিমাপ করি। ত্রিভুজগুলিকে কোণ দ্বারা শ্রেণিবদ্ধ করা যেতে পারে, যেমন:
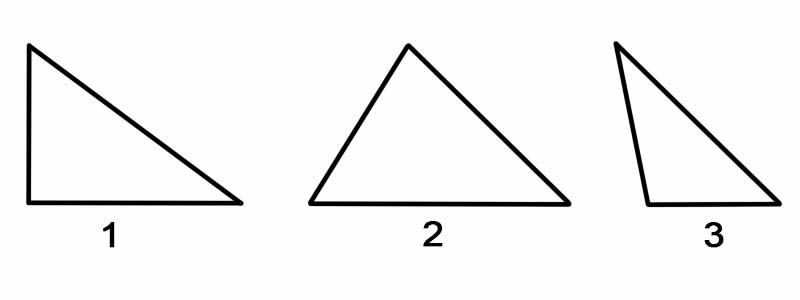
ত্রিভুজগুলিকে তাদের বাহু অনুসারে শ্রেণিবদ্ধ করতে, আমরা এর প্রতিটি বাহুর দৈর্ঘ্য পরিমাপ করি। ত্রিভুজগুলিকে তাদের পক্ষ দ্বারা শ্রেণীবদ্ধ করা যেতে পারে, যেমন:
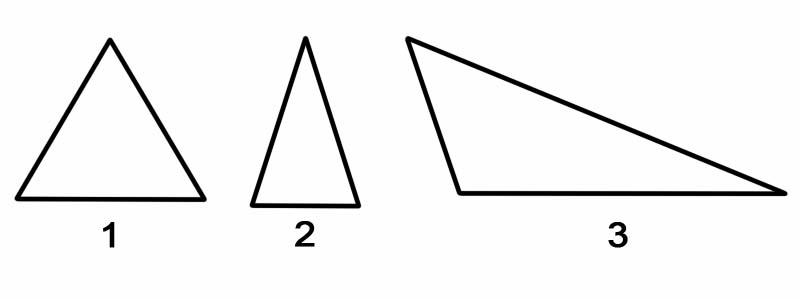
মনে রাখবেন: একটি ত্রিভুজ সর্বদা দুটি সমকোণী ত্রিভূজে বিভক্ত হতে পারে, তার নির্বিশেষে।
ত্রিভুজ হল বহুভুজ যার সর্বনিম্ন সংখ্যা রয়েছে।
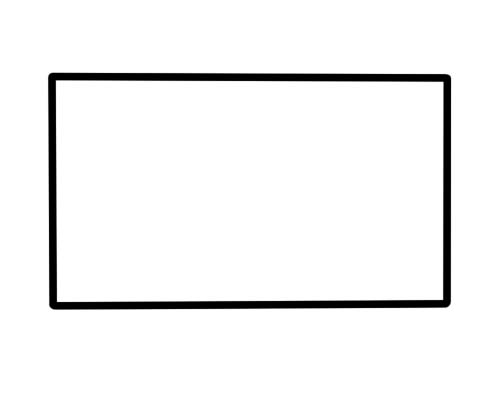
আয়তক্ষেত্র এমন একটি আকৃতি যার sides টি বাহু, ver টি শীর্ষ এবং 4 টি কোণ রয়েছে। বিপরীত দিক সমান্তরাল এবং দৈর্ঘ্যে সমান। সমস্ত 4 কোণ 90 ডিগ্রী পরিমাপ করে।
টেবিল, বাক্স, বই, দরজা, এবং কাগজ দেখতে আয়তক্ষেত্রের মতো।

রম্বস একটি আকৃতি যা 4 টি সরলরেখা দ্বারা গঠিত। এর 4 বাহু একই দৈর্ঘ্য পরিমাপ করে কিন্তু, আয়তক্ষেত্রের বিপরীতে, সমস্ত 4 কোণের কোনটিই 90 ডিগ্রি পরিমাপ করে না। একটি রম্বস দেখতে হীরার মতো। বিপরীত দিক সমান্তরাল এবং বিপরীত কোণ সমান। একটি রম্বসের দুটি কর্ণ একে অপরের লম্ব।

একটি বর্গ হল একটি দ্বিমাত্রিক চিত্র যার চারটি বাহুর দৈর্ঘ্য সমান এবং দুটি বিপরীত দিক একে অপরের সমান্তরাল। এটি এক প্রকার আয়তক্ষেত্র এবং রম্বস (নিচে আলোচনা করা হয়েছে)। একটি বর্গক্ষেত্রের 4 টি অভ্যন্তরীণ কোণ 90º, অথবা অন্য কথায়, সেগুলো সমকোণ। যখন সব কোণ একসাথে যোগ করা হয়, তারা 360º পর্যন্ত যোগ করে। একটি বর্গক্ষেত্রের দুটি কর্ণ দৈর্ঘ্যে সমান এবং যে বিন্দুটি তারা অতিক্রম করে তা হল বর্গটির কেন্দ্র।
মনে রাখবেন: একটি বর্গক্ষেত্র সবসময় একটি রম্বস কিন্তু একটি রম্বস সবসময় একটি বর্গক্ষেত্র নয়। যদি একটি রম্বসের প্রতিটি কোণ 90o হয়, তবেই এটি একটি বর্গক্ষেত্র।
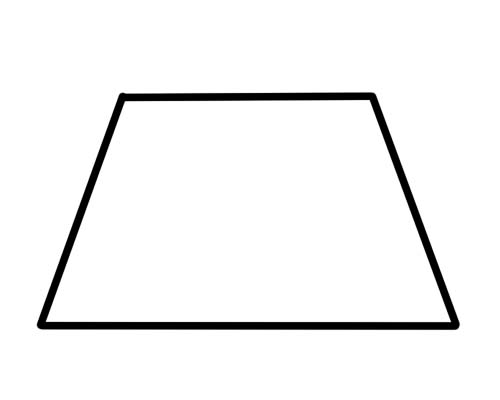
একটি ট্র্যাপিজিয়াম একটি চতুর্ভুজ যার মাত্র দুটি বাহু সমান্তরাল।
এটাই. কোন পক্ষকেই সমান (বা সমান) হতে হবে না এবং কোন কোণকেও সমান হতে হবে না। কর্ণগুলির সাথে বিশেষ কিছু ঘটে না। একটি বিশেষ ধরনের ট্রাপিজিয়াম হল 'আইসোসেলস ট্র্যাপিজিয়াম' যার একই দৈর্ঘ্যের বিপরীত দিক এবং একই পরিমাপের বিপরীত কোণ রয়েছে। কর্ণগুলোও সমান দৈর্ঘ্যের।
একটি সমদ্বিবাহু ত্রিভূজে, পার্শ্ববর্তী কোণগুলি (একে অপরের পাশের কোণ) পরিপূরক। এর মানে হল তারা 180 ডিগ্রী পর্যন্ত যোগ করে।
একটি ট্র্যাপিজিয়াম সমান্তরাল নয় কারণ বিপরীত দিকের একটি মাত্র জোড়া সমান্তরাল।
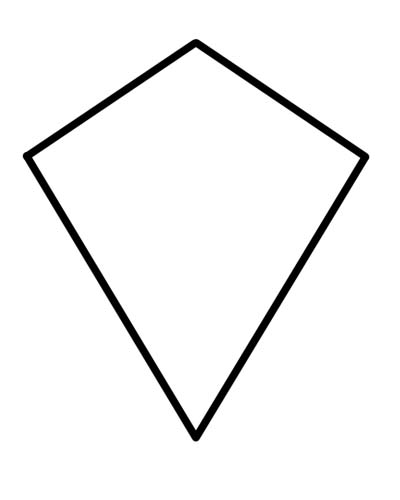
একটি ঘুড়ি হল একটি চতুর্ভুজ যা সমান ধারাবাহিক বাহুর ঠিক দুটি জোড়া বা যার মধ্যে পরপর দুইটি বিচ্ছিন্ন জোড়া একসঙ্গে থাকে (বিচ্ছিন্ন জোড়া মানে যে এক জোড়া উভয় জোড়ায় ব্যবহার করা যায় না)।
আপনার জানা দরকার যে প্রতিটি রম্বস একটি ঘুড়ি, যেহেতু রম্বস একটি ঘুড়ির সমস্ত বৈশিষ্ট্যকে সন্তুষ্ট করে। বিপরীত দিক সমান্তরাল একটি ঘুড়ি অবশ্যই একটি রম্বস হয়ে যায়। সুতরাং প্রতিটি রম্বস একটি ঘুড়ি কিন্তু বিপরীত নয়। একটি ঘুড়ি সমান্তরাল নয় কারণ বিপরীত দিকগুলি একে অপরের সমান্তরাল নয়।
চতুর্ভুজ-একটি চতুর্ভুজ চিত্রকে চতুর্ভুজ বলে
সমান্তরালগ্রাম - একটি সমান্তরালোগ্রাম হল সমতল আকৃতি যার বিপরীত দিক সমান্তরাল এবং দৈর্ঘ্যে সমান।
সুতরাং, আয়তক্ষেত্র, বর্গক্ষেত্র, রম্বস, ট্রাপিজিয়াম এবং ঘুড়ির আকার চতুর্ভুজ কারণ তাদের প্রত্যেকটির চারটি দিক রয়েছে।
যাইহোক, শুধুমাত্র আয়তক্ষেত্র, বর্গক্ষেত্র এবং রম্বস সমান্তরাল।
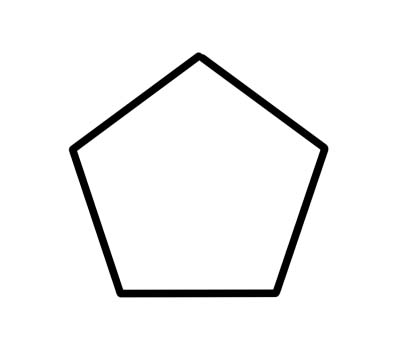
পেন্টাগন হল 5 টি পার্শ্ববিশিষ্ট বহুভুজ যার ভিতরের পাঁচটি কোণ 540 ডিগ্রি যোগ করে। নিয়মিত পেন্টাগনের সমান দৈর্ঘ্যের দিক থাকে এবং প্রতিটি অভ্যন্তর কোণ 108 ডিগ্রী হয়।
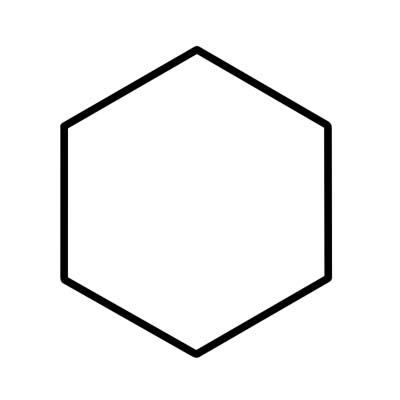
একটি ষড়ভুজ হল একটি--পার্শ্ববিশিষ্ট বহুভুজ যা ছয়টি অভ্যন্তরীণ কোণ যা 720 ডিগ্রি যোগ করে। অনিয়মিত ষড়ভুজের বিভিন্ন দৈর্ঘ্যের দিক রয়েছে।
একটি নিয়মিত ষড়ভুজের সমান দৈর্ঘ্য থাকে এবং প্রতিটি অভ্যন্তর কোণ 120 ডিগ্রী হয়। একটি নিয়মিত ষড়ভুজ equ০ ডিগ্রি সমান প্রতিটি কেন্দ্রীয় কোণ সহ ছয়টি সমবাহু ত্রিভুজ দিয়ে গঠিত।
[ছবি সন্নিবেশ করান: ষড়ভুজটি ছয়টি ত্রিভূজে বিভক্ত এবং একটি কেন্দ্রীয় কোণ যা 60 ডিগ্রি পরিমাপ করে]
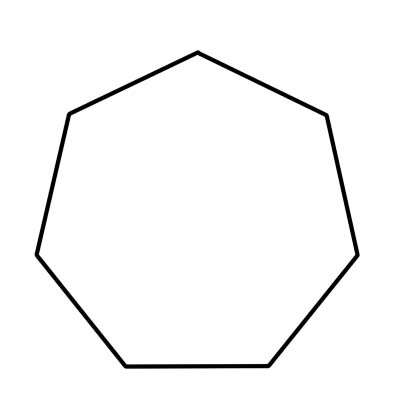
একটি হেপটাগন একটি সাত পার্শ্বযুক্ত বহুভুজ। সাতটি দিকের পাশাপাশি, একটি হেপ্টাগনের সাতটি শীর্ষ এবং কোণ রয়েছে। সমস্ত সাতটি অভ্যন্তর কোণ 900 ডিগ্রি যোগ করে। নিয়মিত হেপটাগনের প্রতিটি অভ্যন্তর কোণের পরিমাপ প্রায় 128.57 ডিগ্রি বা প্রায় 129 ডিগ্রি।
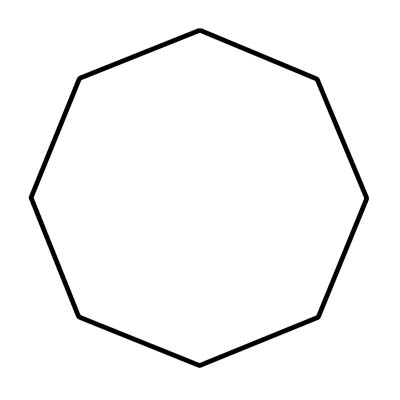
একটি অষ্টভুজ হল একটি জ্যামিতিক আকৃতি যার আটটি বাহু এবং আটটি কোণ রয়েছে। অক্টাগনের অবশ্যই সোজা দিক থাকতে হবে যা সংযোগ করে; তারা বাঁকা বা সংযোগ বিচ্ছিন্ন করা যাবে না। আপনি প্রায়ই বাস্তব জীবনে অষ্টভুজগুলিকে স্টপ চিহ্নের আকারে দেখতে পাবেন। একটি নিয়মিত অষ্টভুজের আটটি অভ্যন্তর কোণের প্রত্যেকটির পরিমাপ প্রায় 108 ডিগ্রি। একটি উত্তল অষ্টভুজের কোন কোণ ভিতরের দিকে নির্দেশ করে না। আরও স্পষ্টভাবে, কোন অভ্যন্তরীণ কোণ 180 than এর বেশি হতে পারে না। যখন কোন অভ্যন্তরীণ কোণ 180 than এর চেয়ে বড় হয় তখন এটি অবতল
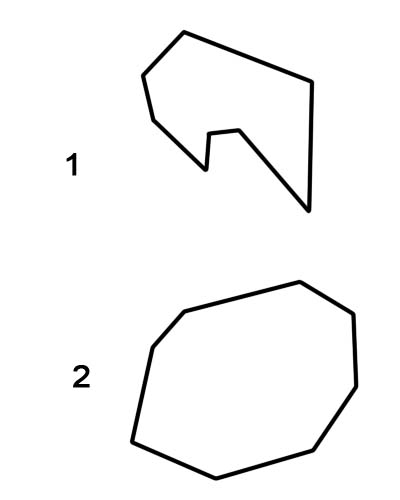
1. অবতল অষ্টভুজ
2. উত্তল অষ্টভুজ
এটা লক্ষ করা গুরুত্বপূর্ণ যে নিয়মিত অষ্টভুজগুলিকে সর্বদা উত্তল অষ্টভুজ হিসাবে শ্রেণীবদ্ধ করা হয়, যখন অনিয়মিত অষ্টভুজগুলি অবতল বা উত্তল হতে পারে।
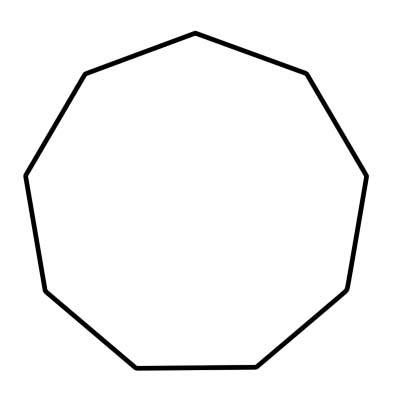
একটি ননকোণ হল একটি বহুভুজ যার 9 বাহু এবং 9 অভ্যন্তরীণ কোণ যা 1260 ডিগ্রী যোগ করে। একটি নিয়মিত ননকোণের একই দৈর্ঘ্যের সব দিক আছে এবং সমস্ত অভ্যন্তর কোণ একই আকারের। নিয়মিত ননগনের কোণের পরিমাপ 140 ডিগ্রি। একটি ননকোণ tri টি ত্রিভুজ দিয়ে গঠিত যার প্রতিটি কেন্দ্রীয় কোণের পরিমাপ 40০ ডিগ্রি সমান।
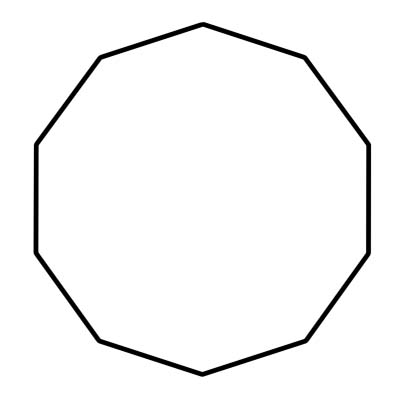
একটি দশভুজ একটি 10-পার্শ্বযুক্ত বহুভুজ। এটিতে দশটি শীর্ষবিন্দুও রয়েছে - যেখানে উভয় পক্ষ মিলিত হয় - এবং কোণ। দশভুজের অভ্যন্তরীণ কোণের সমষ্টি 1440 ডিগ্রি। একটি নিয়মিত দশভুজের সামঞ্জস্যপূর্ণ দিক এবং কোণ থাকে। প্রতিটি কোণ 144 ডিগ্রী পরিমাপ করে। দশকোণটি 10 টি ত্রিভুজ দিয়ে গঠিত যার কেন্দ্রীয় কোণ 36 ডিগ্রির সমান।
যেসব আকৃতি তিন দিক দিয়ে পরিমাপ করা যায় তাকে ত্রিমাত্রিক আকার বা 3D আকৃতি বলে। 3D আকৃতিগুলিকে কঠিন আকারও বলা হয়। 3D আকৃতির তিনটি পরিমাপ হল - দৈর্ঘ্য, প্রস্থ এবং উচ্চতা (বা গভীরতা বা বেধ)।
3D আকৃতি 2D আকৃতির থেকে আলাদা কারণ তাদের পুরুত্ব রয়েছে। আমাদের দৈনন্দিন জীবন থেকে 3D আকৃতির কিছু উদাহরণ হল:
ত্রিমাত্রিক আকারের শীর্ষ, মুখ এবং প্রান্ত রয়েছে।
প্রিজম হল এক ধরনের ত্রিমাত্রিক (3D) আকৃতির সমতল দিক। এর দুটি প্রান্ত রয়েছে যা একই আকৃতি এবং আকার (এবং একটি 2D আকৃতির মত দেখতে)। এটি একই ক্রস-সেকশনে রয়েছে যার প্রান্ত থেকে শেষ পর্যন্ত আকৃতি রয়েছে; এর মানে হল যে আপনি যদি এটি কেটে ফেলেন তবে আপনি উভয় পাশে একই 2D আকৃতি দেখতে পাবেন।
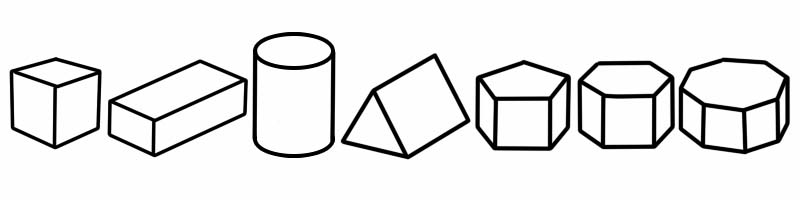
3D আকৃতি | প্রান্ত সংখ্যা | মুখের সংখ্যা | শিরোনাম সংখ্যা |
ঘনক | 12 | 6 | 8 |
কিউবয়েড | 12 | 6 | 8 |
সিলিন্ডার | 2 | 3 | 0 |
ত্রিদলীয় প্রিজম | 9 | 5 (2 ত্রিভুজ, 3 আয়তক্ষেত্র) | 6 |
পেন্টাগোনাল প্রিজম | 15 | 7 | 10 |
ষড়ভুজ প্রিজম | 18 | 8 | 12 |
অষ্টভুজ প্রিজম | 24 | 10 | 16 |
একটি পিরামিডও একটি ত্রিমাত্রিক (3D) আকৃতি। এটির একটি বহুভুজ ভিত্তি এবং সমতল (ত্রিভুজাকার) দিক রয়েছে যা একটি সাধারণ বিন্দুতে (এপেক্স নামে পরিচিত) যোগ দেয়। যখন 'পিরামিড' শব্দটি উল্লেখ করা হয়, তখন আমাদের মনে প্রথম যে বিষয়টি আসে তা হলো মিশরের বিখ্যাত পিরামিড। মিসরীয় পিরামিডগুলি বর্গ ভিত্তিক পিরামিড, কিন্তু আরও বেশ কয়েকটি প্রকারের পিরামিড রয়েছে, যার প্রত্যেকটির ভিত্তি আলাদা আলাদা বহুভুজ রয়েছে।
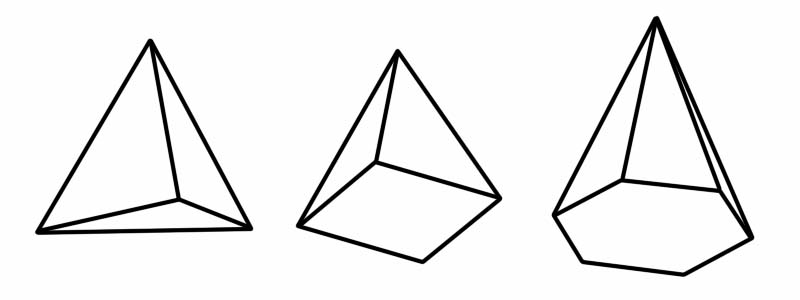
আকৃতি | প্রান্ত সংখ্যা | মুখের সংখ্যা | শিরোনাম সংখ্যা |
টেট্রাহেড্রন | 6 | 4 | 4 |
স্কয়ার পিরামিড | 8 | 5 | 5 |
ষড়ভুজাকার পিরামিড | 12 | 7 | 7 |
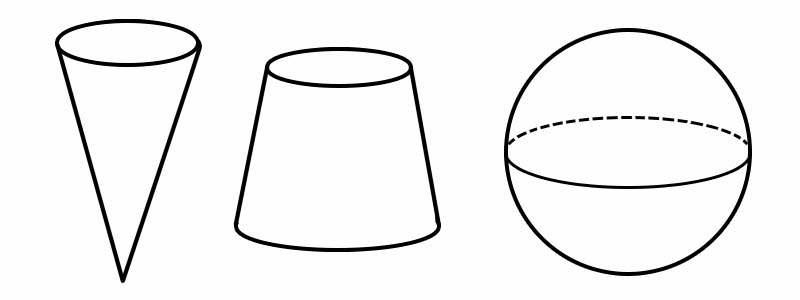
আকৃতি | প্রান্ত সংখ্যা | মুখের সংখ্যা | শিরোনাম সংখ্যা |
শঙ্কু | ঘ | 2 | ঘ |
হতাশা | 2 | 3 | 0 |
গোলক | 0 | ঘ | 0 |