अपने आस-पास की विभिन्न वस्तुओं का निरीक्षण करें। वे विभिन्न आकृतियों और आकारों में आते हैं। कुछ समान हैं और कुछ अलग हैं। यद्यपि हम सभी वस्तुओं के आकार का सटीक नाम नहीं दे सकते हैं, गणित में हम बड़े पैमाने पर 2D आकृतियों और 3D आकृतियों के बारे में बात करते हैं। आइए उनके बारे में और जानें!
2D आकार शब्द "द्वि-आयामी" आकार को संदर्भित करता है। एक ज्यामितीय आकृति जिसमें दो आयाम होते हैं - केवल लंबाई और चौड़ाई एक 2D आकृति होती है। द्वि-आयामी आकृतियों की कोई मोटाई नहीं होती है। भुजाएँ सीधी या घुमावदार रेखाओं से बनी होती हैं। उनके पास कितनी भी भुजाएँ हो सकती हैं।
दो आयामों की अवधारणा को एक सपाट सतह के रूप में माना जा सकता है, जिस पर कोई भी कहीं भी जा सकता है। समतल सतह को समतल के रूप में जाना जाता है। एक 2डी आकार एक ऐसी चीज है जो हमेशा कागज की एक शीट पर होती है। इसकी कोई ऊंचाई नहीं है, और इसलिए यह कागज के टुकड़े से ऊपर नहीं गिरता है। 2डी आकृतियों को समतल आकृतियों या समतल आकृतियों के रूप में भी जाना जाता है।
2D आकृतियों का क्षेत्रफल तो होता है लेकिन आयतन नहीं होता।
आकृतियों की विशेषताओं को रेखांकित करने के लिए तीन महत्वपूर्ण शब्द हैं:
भुजाएँ - एक रेखा खंड जो 2-आयामी आकृति पर एक आकृति बनाता है।
कोने - एक आकृति का एक कोना।
कोण - ज्यामिति में, एक कोण को एक सामान्य समापन बिंदु पर दो रेखाओं के मिलने से बनने वाली आकृति के रूप में परिभाषित किया जा सकता है।
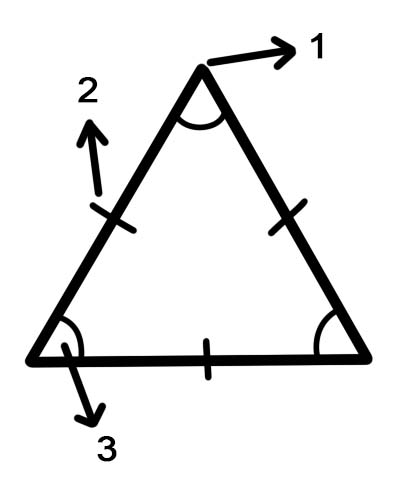
1. शीर्ष
2. पक्ष
3. कोण
आइए विभिन्न 2D आकृतियों पर चर्चा करें।

एक वृत्त एक गोल आकार की आकृति है जिसमें कोई कोना या किनारा नहीं होता है। हम अपने चारों ओर कार के टायर, दीवार घड़ी और लॉलीपॉप में वृत्त का आकार पा सकते हैं। एक वृत्त का केंद्र एक वृत्त का केंद्र बिंदु होता है, जहाँ से वृत्त के सभी बिंदुओं की दूरी समान होती है। केंद्र से वृत्त के किसी भी बिंदु तक की दूरी को त्रिज्या कहा जाता है। यदि हम केंद्र से गुजरने वाले वृत्त के आर-पार की दूरी पर विचार करें, तो वह व्यास है। वृत्त के चारों ओर की दूरी वृत्त की परिधि कहलाती है।
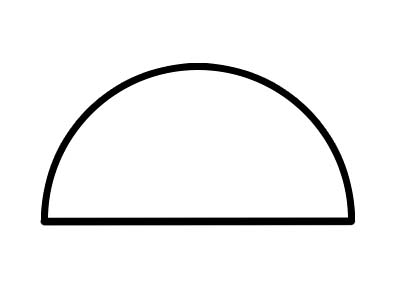
एक अर्धवृत्त एक आधा वृत्त है, जो एक व्यास रेखा के साथ एक पूरे वृत्त को काटकर बनाया गया है, जैसा कि ऊपर दिखाया गया है। वृत्त का कोई भी व्यास इसे दो बराबर अर्धवृत्तों में काटता है। अर्धवृत्त का पूर्ण चाप सदैव 180° मापता है। यदि एक कुकी को दो हिस्सों में काटा जाता है, तो प्रत्येक आधा अर्धवृत्त होता है।

एक अंडाकार में अंडे का रूप, आकार या रूपरेखा होती है। एक अंडाकार का कोई सीधा पक्ष और कोई कोना नहीं होता है, लेकिन इसमें 1 चेहरा होता है, जिसे देखने पर पता लगाया जा सकता है या एक सपाट आकार के रूप में देखा जा सकता है।
बहुभुज एक समतल आकृति होती है जिसमें सीधी रेखाएँ होती हैं। उदाहरणों में त्रिभुज, चतुर्भुज, पंचकोण, षट्भुज आदि शामिल हैं। एक नियमित बहुभुज में सभी भुजाएँ समान होती हैं और सभी कोण समान होते हैं। अन्यथा, यह एक अनियमित बहुभुज है।
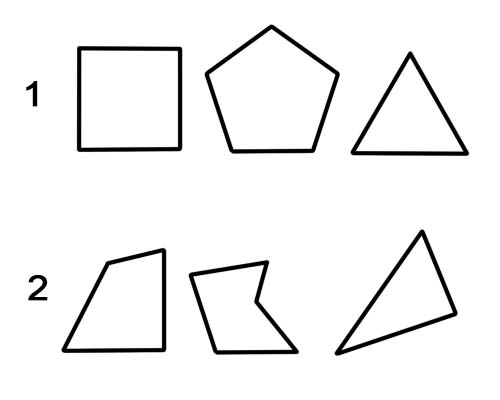
1. नियमित बहुभुज।
2. अनियमित बहुभुज।
वृत्त और आकृतियाँ जिनमें वक्र शामिल हैं, बहुभुज नहीं हैं - एक बहुभुज, परिभाषा के अनुसार, सीधी रेखाओं से बना होता है।

ज्यामिति में, त्रिभुज तीन सीधी रेखाओं वाला एक बंद, द्वि-आयामी आकार होता है। एक त्रिभुज भी एक बहुभुज है।
हम एक झंडे, सड़क के किनारे एक साइनबोर्ड और एक सैंडविच में त्रिभुज का आकार पा सकते हैं।
एक त्रिभुज में तीन भुजाएँ, तीन शीर्ष और तीन कोण होते हैं।
त्रिभुज के तीनों अंतः कोणों का योग सदैव 180° होता है। किसी त्रिभुज की दो भुजाओं की लंबाई का योग हमेशा तीसरी भुजा की लंबाई से अधिक होता है।
त्रिभुजों को उनके कोणों के अनुसार वर्गीकृत करने के लिए, हम इसके प्रत्येक आंतरिक कोण को मापते हैं। त्रिभुजों को कोणों द्वारा वर्गीकृत किया जा सकता है, जैसे:
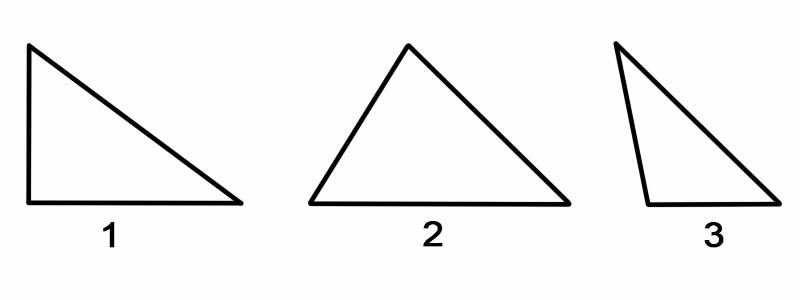
त्रिभुजों को उनकी भुजाओं के अनुसार वर्गीकृत करने के लिए, हम इसकी प्रत्येक भुजा की लंबाई मापते हैं। त्रिभुजों को उनकी भुजाओं द्वारा वर्गीकृत किया जा सकता है, जैसे:
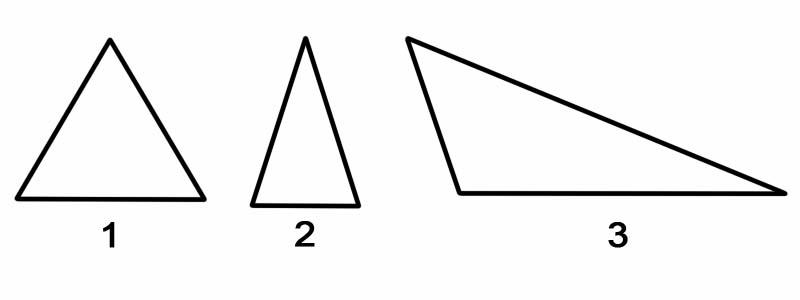
याद रखें: एक त्रिभुज को हमेशा दो समकोण त्रिभुजों में विभाजित किया जा सकता है, चाहे उसका अभिविन्यास कुछ भी हो।
त्रिभुज ऐसे बहुभुज होते हैं जिनकी भुजाओं की संख्या सबसे कम होती है।
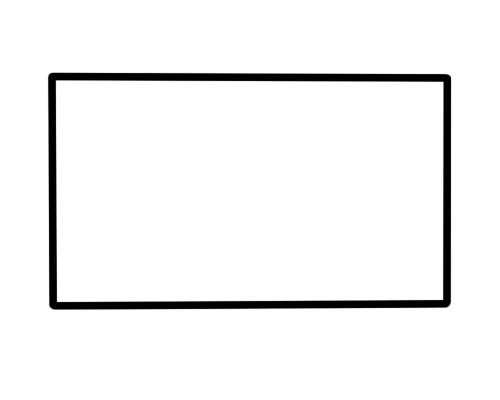
आयत एक ऐसी आकृति है जिसमें 4 भुजाएँ, 4 शीर्ष और 4 कोण होते हैं। विपरीत भुजाएँ समानांतर और लंबाई में समान हैं। सभी 4 कोण 90 डिग्री मापते हैं।
टेबल, बक्से, किताबें, दरवाजे और कागज आयताकार की तरह दिखते हैं।

समचतुर्भुज 4 सीधी रेखाओं से बनी एक आकृति है। इसकी 4 भुजाएँ समान लंबाई मापती हैं, लेकिन आयत के विपरीत, सभी 4 कोणों में से कोई भी 90 डिग्री नहीं मापता है। समचतुर्भुज हीरे जैसा दिखता है। सम्मुख भुजाएँ समान्तर होती हैं और सम्मुख कोण बराबर होते हैं। एक समचतुर्भुज के दो विकर्ण परस्पर लंबवत होते हैं।

एक वर्ग एक द्वि-आयामी आकृति है जिसकी सभी चार भुजाएँ लंबाई में समान हैं और दो विपरीत भुजाएँ एक दूसरे के समानांतर हैं। यह एक प्रकार का आयत और समचतुर्भुज है (नीचे चर्चा की गई है)। एक वर्ग के 4 आंतरिक कोण 90º होते हैं, या दूसरे शब्दों में, वे समकोण होते हैं। जब सभी कोणों को एक साथ जोड़ दिया जाता है, तो वे 360º तक जुड़ जाते हैं। एक वर्ग के दो विकर्ण लंबाई में बराबर होते हैं और जिस बिंदु पर वे पार करते हैं वह वर्ग का केंद्र होता है।
याद रखें: एक वर्ग हमेशा एक समचतुर्भुज होता है लेकिन एक समचतुर्भुज हमेशा एक वर्ग नहीं होता है। यदि किसी समचतुर्भुज का प्रत्येक कोण 90° का हो, तभी वह एक वर्ग होता है।
एक समलम्ब चतुर्भुज एक चतुर्भुज है जिसकी केवल दो भुजाएँ समानांतर हैं।
बस, इतना ही। किसी भी पक्ष को सर्वांगसम (या बराबर) होने की आवश्यकता नहीं है और किसी भी कोण को सर्वांगसम होने की आवश्यकता नहीं है। विकर्णों के साथ कुछ खास नहीं होता है। एक विशेष प्रकार का समलम्ब चतुर्भुज 'समद्विबाहु समलम्ब' है जिसमें समान लंबाई के विपरीत भुजाएँ और समान माप के विपरीत कोण होते हैं। विकर्ण भी समान लंबाई के होते हैं।
एक समद्विबाहु त्रिभुज में, भुजाओं के साथ लगे आसन्न कोण (एक दूसरे के बगल के कोण) पूरक होते हैं। इसका मतलब है कि वे 180 डिग्री तक जोड़ते हैं।
समलम्ब चतुर्भुज समांतर चतुर्भुज नहीं है क्योंकि सम्मुख भुजाओं का केवल एक युग्म समांतर होता है।
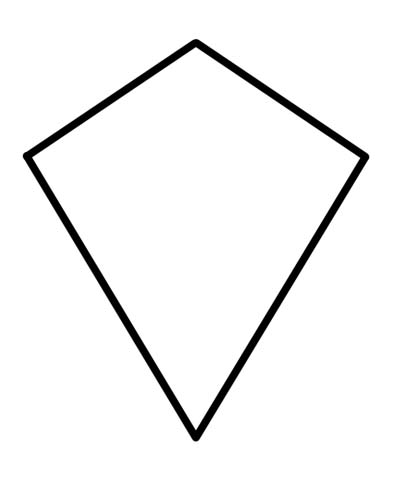
पतंग एक चतुर्भुज होता है जिसमें समान क्रमागत भुजा के ठीक दो जोड़े होते हैं या जिसमें लगातार भुजाओं के दो असंयुक्त जोड़े सर्वांगसम होते हैं (विघटित जोड़े का अर्थ है कि दोनों जोड़ों में एक पक्ष का उपयोग नहीं किया जा सकता है)।
आपको यह जानना आवश्यक है कि प्रत्येक समचतुर्भुज एक पतंग है, क्योंकि समचतुर्भुज एक पतंग के सभी गुणों को संतुष्ट करता है। विपरीत भुजाओं वाली पतंग निश्चित रूप से समचतुर्भुज बन जाती है। इस प्रकार प्रत्येक समचतुर्भुज एक पतंग है लेकिन इसके विपरीत नहीं। पतंग एक समांतर चतुर्भुज नहीं है क्योंकि विपरीत भुजाएँ एक दूसरे के समानांतर नहीं होती हैं।
चतुर्भुज - चार भुजाओं वाली आकृति को चतुर्भुज कहते हैं
समांतर चतुर्भुज - एक समांतर चतुर्भुज एक सपाट आकृति होती है जिसकी विपरीत भुजाएँ समानांतर और लंबाई में बराबर होती हैं।
इस प्रकार, आयत, वर्ग, समचतुर्भुज, समलंब और पतंग की आकृतियाँ चतुर्भुज हैं क्योंकि इनकी प्रत्येक में चार भुजाएँ होती हैं।
हालाँकि, केवल आयत, वर्ग और समचतुर्भुज समांतर चतुर्भुज हैं।
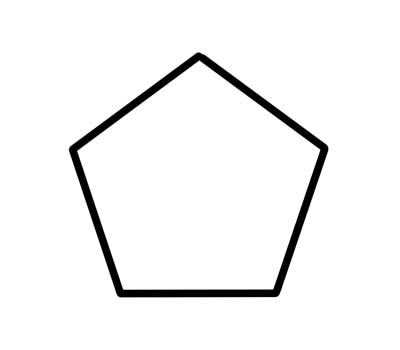
एक पेंटागन एक 5 भुजा वाला बहुभुज है जिसमें पांच आंतरिक कोण होते हैं जो 540 डिग्री जोड़ते हैं। नियमित पंचभुज की भुजाएँ समान लंबाई की होती हैं और प्रत्येक आंतरिक कोण 108 डिग्री का होता है।
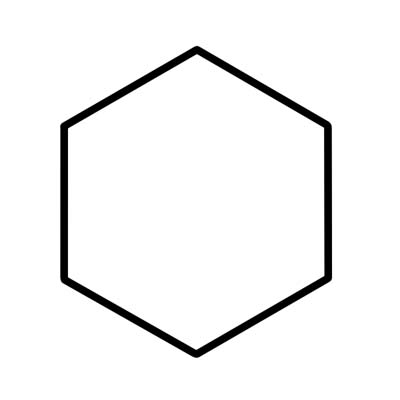
एक षट्भुज एक 6-पक्षीय बहुभुज है जिसमें छह आंतरिक कोण होते हैं जो 720 डिग्री जोड़ते हैं। अनियमित षट्भुज में विभिन्न लंबाई के पक्ष होते हैं।
एक नियमित षट्भुज की भुजाएँ समान लंबाई की होती हैं और प्रत्येक आंतरिक कोण 120 डिग्री का होता है। एक नियमित षट्भुज छह समबाहु त्रिभुजों से बना होता है जिनका प्रत्येक केंद्रीय कोण 60 डिग्री के बराबर होता है।
[छवि डालें: षट्भुज छह त्रिकोणों में विभाजित है और एक केंद्रीय कोण 60 डिग्री मापता है]
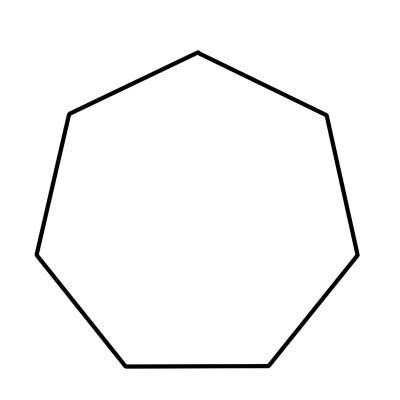
एक सप्तभुज सात भुजाओं वाला बहुभुज है। सात भुजाओं के साथ, एक समभुज में सात शीर्ष और कोण होते हैं। सभी सात आंतरिक कोणों का योग 900 डिग्री होता है। एक नियमित सप्तभुज के प्रत्येक आंतरिक कोण का माप लगभग 128.57 डिग्री या लगभग 129 डिग्री है।
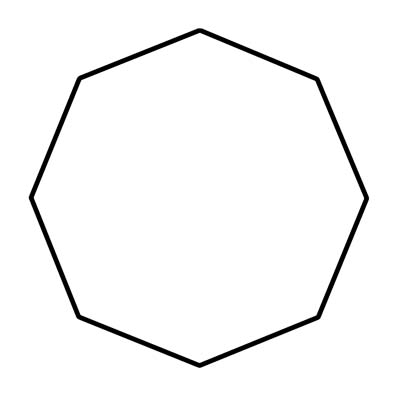
अष्टभुज एक ज्यामितीय आकृति है जिसमें आठ भुजाएँ और आठ कोण होते हैं। अष्टभुज के सीधे पक्ष होने चाहिए जो जुड़ते हैं; उन्हें घुमावदार या डिस्कनेक्ट नहीं किया जा सकता है। आपने अक्सर वास्तविक जीवन में अष्टभुजों को स्टॉप साइन के आकार में देखा होगा। एक नियमित अष्टभुज के आठ आंतरिक कोणों में से प्रत्येक का माप लगभग 108 डिग्री है। एक उत्तल अष्टभुज में कोई कोण नहीं होता जो अंदर की ओर इंगित करता हो। अधिक सटीक रूप से, कोई भी आंतरिक कोण 180° से अधिक नहीं हो सकता है। जब कोई आंतरिक कोण 180° से अधिक होता है तो वह अवतल होता है
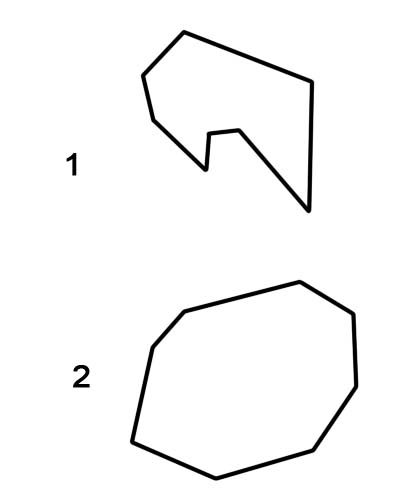
1. अवतल अष्टभुज
2. उत्तल अष्टभुज
यह ध्यान रखना महत्वपूर्ण है कि नियमित अष्टकोण को हमेशा उत्तल अष्टकोण के रूप में वर्गीकृत किया जाता है, जबकि अनियमित अष्टकोण या तो अवतल या उत्तल हो सकते हैं।
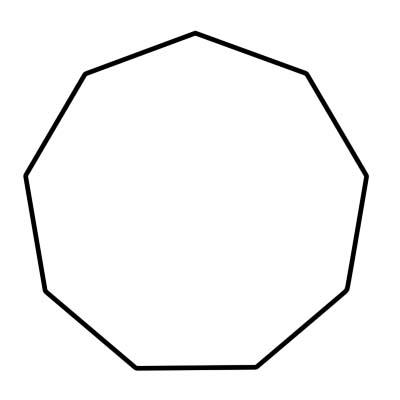
एक नॉनगोन 9 भुजाओं और 9 आंतरिक कोणों वाला बहुभुज है जो 1260 डिग्री जोड़ता है। एक नियमित नॉनगोन की सभी भुजाएँ समान लंबाई की होती हैं और सभी आंतरिक कोण समान आकार के होते हैं। एक नियमित गैर-कोण के कोण का माप 140 डिग्री है। एक गैर-कोण 9 त्रिभुजों से बना होता है जिनका प्रत्येक केंद्रीय कोण 40 डिग्री के बराबर होता है।
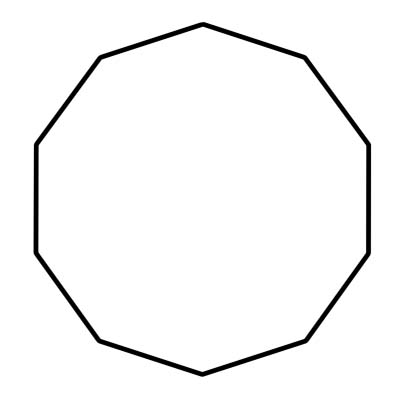
एक दशकोण एक 10-पक्षीय बहुभुज है। इसके दस कोने भी हैं - जहाँ पर भुजाएँ मिलती हैं - और कोण। एक दशमांश के अंत:कोणों का योग 1440 डिग्री होता है। एक नियमित दशमांश में सर्वांगसम भुजाएँ और कोण होते हैं। प्रत्येक कोण 144 डिग्री मापता है। एक दशभुज 10 त्रिभुजों से बना होता है जिनका केंद्रीय कोण 36 डिग्री के बराबर होता है।
वे आकृतियाँ जिन्हें तीन दिशाओं में मापा जा सकता है, त्रिविमीय आकृतियाँ या 3D आकृतियाँ कहलाती हैं। 3डी आकृतियों को ठोस आकार भी कहा जाता है। 3डी आकृतियों के तीन माप हैं - लंबाई, चौड़ाई और ऊंचाई (या गहराई या मोटाई)।
3D आकृतियाँ 2D आकृतियों से भिन्न होती हैं क्योंकि उनमें मोटाई होती है। हमारे दैनिक जीवन से 3डी आकृतियों के कुछ उदाहरण इस प्रकार हैं:
त्रि-आयामी आकृतियों में कोने, फलक और किनारे होते हैं।
एक प्रिज्म एक प्रकार का त्रि-आयामी (3D) आकार होता है जिसमें सपाट भुजाएँ होती हैं। इसके दो सिरे होते हैं जो समान आकार और आकार के होते हैं (और 2D आकार की तरह दिखते हैं)। इसमें अंत से अंत तक आकार के साथ-साथ एक ही क्रॉस-सेक्शन है; इसका मतलब है कि यदि आप इसे काटते हैं तो आपको दोनों तरफ समान 2D आकार दिखाई देगा।
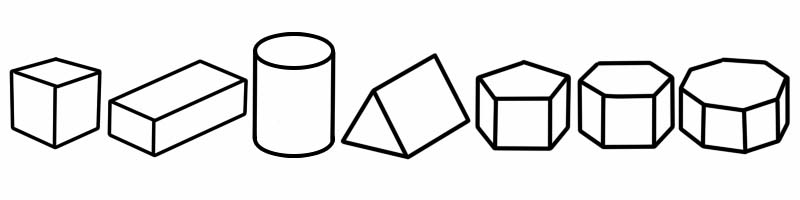
3डी आकार | किनारों की संख्या | चेहरों की संख्या | शीर्षों की संख्या |
घनक्षेत्र | 12 | 6 | 8 |
घनाभ | 12 | 6 | 8 |
सिलेंडर | 2 | 3 | 0 |
त्रिकोणीय प्रिज्म | 9 | 5 (2 त्रिकोण, 3 आयत) | 6 |
पंचकोणीय प्रिज्म | 15 | 7 | 10 |
हेक्सागोनल प्रिज्म | 18 | 8 | 12 |
अष्टकोणीय प्रिज्म | 24 | 10 | 16 |
पिरामिड भी त्रि-आयामी (3D) आकार का होता है। इसमें एक बहुभुज आधार और समतल (त्रिकोणीय) भुजाएँ होती हैं जो एक सामान्य बिंदु (जिसे शीर्ष कहा जाता है) पर जुड़ती हैं। जब 'पिरामिड' शब्द का जिक्र होता है तो सबसे पहले जो चीज हमारे दिमाग में आती है वह है मिस्र के प्रसिद्ध पिरामिड। मिस्र के पिरामिड वर्ग-आधारित पिरामिड हैं, लेकिन कई अन्य प्रकार के पिरामिड हैं, जिनमें से प्रत्येक के आधार के रूप में एक अलग बहुभुज है।
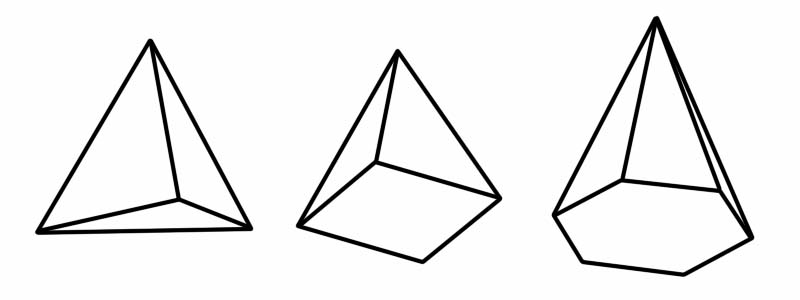
आकार | किनारों की संख्या | चेहरों की संख्या | शीर्षों की संख्या |
चतुर्पाश्वीय | 6 | 4 | 4 |
चौकोर पिरामिड | 8 | 5 | 5 |
हेक्सागोनल पिरामिड | 12 | 7 | 7 |
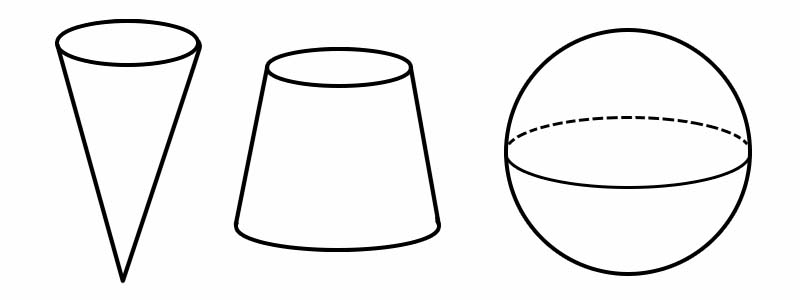
आकार | किनारों की संख्या | चेहरों की संख्या | शीर्षों की संख्या |
शंकु | 1 | 2 | 1 |
छिन्नक | 2 | 3 | 0 |
वृत्त | 0 | 1 | 0 |