あなたの周りのさまざまなオブジェクトを観察してください。さまざまな形やサイズがあります。同じものもあれば、異なるものもあります。すべてのオブジェクトの形状を正確に指定することはできませんが、数学では主に 2D 形状と 3D 形状について話します。それらについてもっと学びましょう!
2D形状という言葉は、「2次元」形状を指します。長さと幅だけの 2 つの次元を持つ幾何学的図形は 2D 形状です。 2 次元形状には厚みがありません。側面は直線または曲線で構成されています。それらは任意の数の面を持つことができます。
2 次元の概念は、人がどこにでも移動できる平面と考えることができます。平らな面は平面として知られています。 2D 形状は常に紙の上にあるものです。高さがないため、紙の上に落ちません。 2D 形状は、平面形状または平面図形とも呼ばれます。
2D 形状には面積がありますが、体積はありません。
形状の特徴を概説するための 3 つの重要な用語があります。
側面 - 2 次元の図形の形状を形成する線分。
頂点 - 図形の角。
角度 - ジオメトリでは、角度は、共通の終点で交わる 2 つの線によって形成される図形として定義できます。
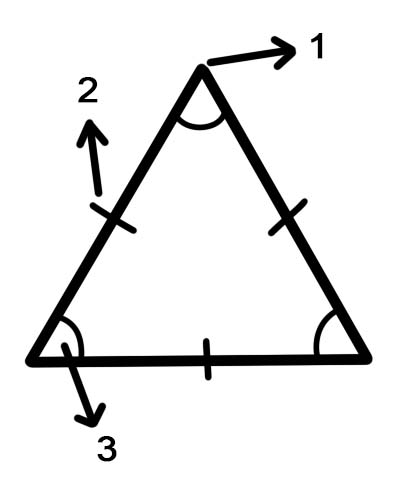
1.頂点
2.側面
3.角度
さまざまな 2D 形状について説明しましょう。

円は、角や縁のない丸い形の図形です。私たちの身の回りには、車のタイヤ、掛け時計、ロリポップなどに円の形が見られます。円の中心は円の中心点であり、そこから円上の点までのすべての距離は等しくなります。円の中心から任意の点までの距離を半径と呼びます。中心を通る円を横切る距離を考えると、それが直径です。円の周りの距離は、円周と呼ばれます。
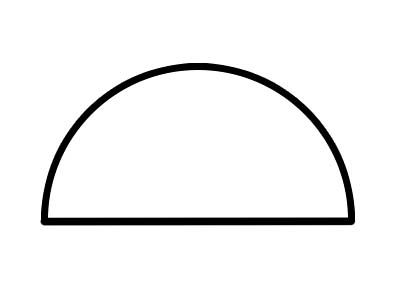
半円は、上の図のように、円全体を直径線に沿って切断することによって形成される半円です。円の任意の直径は、それを 2 つの等しい半円に分割します。半円の完全な円弧は常に 180° です。クッキーを半分に切ると、それぞれが半円になります。

楕円形は、卵の形、形、または輪郭を持っています。楕円形にはまっすぐな辺も角もありませんが、面が 1 つあり、それを見るとトレースしたり、平らな形として見ることができます。
ポリゴンは、直線を持つ平面形状です。例としては、三角形、四角形、五角形、六角形などがあります。正多角形はすべての辺が等しく、すべての角が等しい。それ以外の場合は、不規則な多角形です。
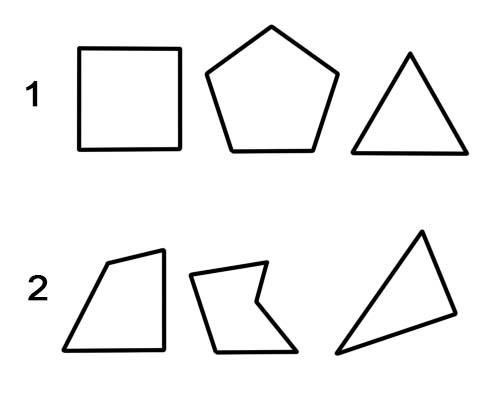
1.正多角形。
2.不規則な多角形。
曲線を含む円や形状は多角形ではありません。定義上、多角形は直線で構成されています。

ジオメトリでは、三角形は 3 本の直線を持つ閉じた 2 次元の形状です。三角形も多角形です。
三角形の形は、旗や道端の看板、サンドイッチなどに見られます。
三角形には、3 つの辺、3 つの頂点、および 3 つの角があります。
三角形の 3 つの内角の和は常に 180° です。三角形の 2 辺の長さの合計は、常に 3 番目の辺の長さよりも大きくなります。
角度によって三角形を分類するには、それぞれの内角を測定します。三角形は角度によって次のように分類できます。
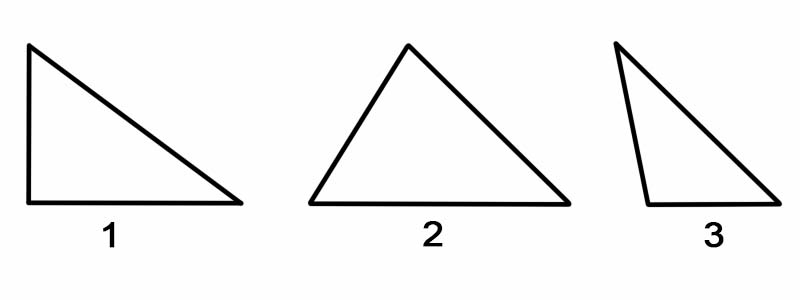
三角形を辺に基づいて分類するには、各辺の長さを測定します。三角形は辺によって次のように分類できます。
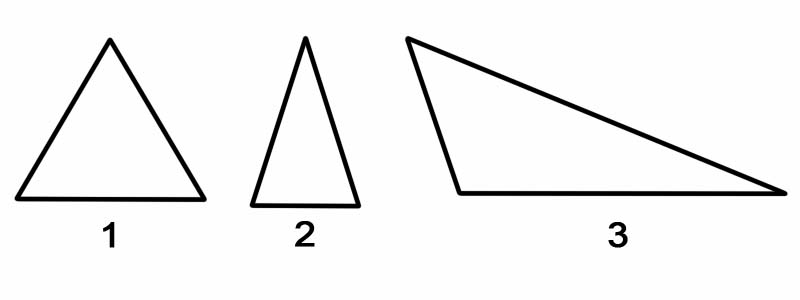
注意: 三角形は、向きに関係なく、常に 2 つの直角三角形に分割できます。
三角形は、辺の数が最も少ない多角形です。
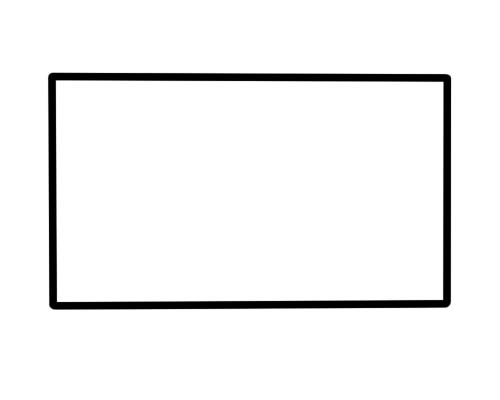
長方形は、4 つの辺、4 つの頂点、および 4 つの角を持つ形状です。対辺は平行で長さが等しい。 4 つの角度はすべて 90 度です。
テーブル、箱、本、ドア、紙は長方形に見えます。

ひし形は4本の直線でできた形です。その 4 辺の長さは同じですが、長方形とは異なり、4 つの角すべてが 90 度になることはありません。ひし形はダイヤモンドのように見えます。対辺は平行で対角は等しい。菱形の 2 つの対角線は互いに垂直です。

正方形は、4 つの辺の長さがすべて等しく、向かい合う 2 つの辺が互いに平行な 2 次元の図形です。これは、長方形とひし形 (後述) の一種です。正方形の 4 つの内角は 90°、つまり直角です。すべての角度を合計すると、360° になります。正方形の 2 つの対角線の長さは等しく、それらが交差する点が正方形の中心です。
覚えておいてください: 正方形は常に菱形ですが、菱形は常に正方形であるとは限りません。ひし形の各角度が 90 度の場合にのみ、それは正方形です。
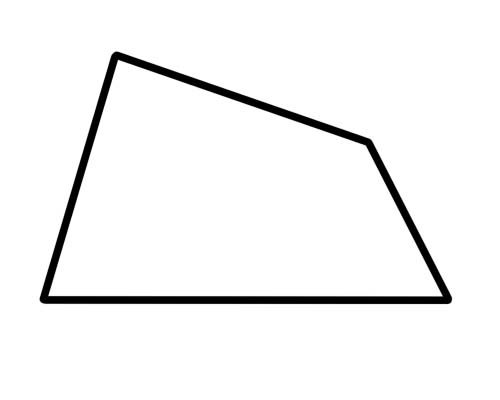
台形は、2 つの辺だけが平行な四角形です。
それでおしまい。辺が合同 (または等しい) である必要はなく、角度が合同である必要もありません。対角線では特別なことは何も起こりません。特殊なタイプの台形は「二等辺台形」で、同じ長さの反対側の辺と同じ大きさの反対側の角度を持っています。対角線も同じ長さです。
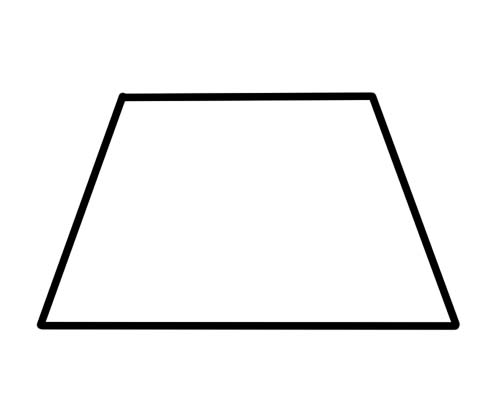
二等辺三角形では、辺に沿って隣接する角 (互いに隣り合う角) は補足的です。これは、合計すると 180 度になることを意味します。
台形は平行四辺形ではありません。なぜなら、対辺は 1 組しか平行ではないからです。
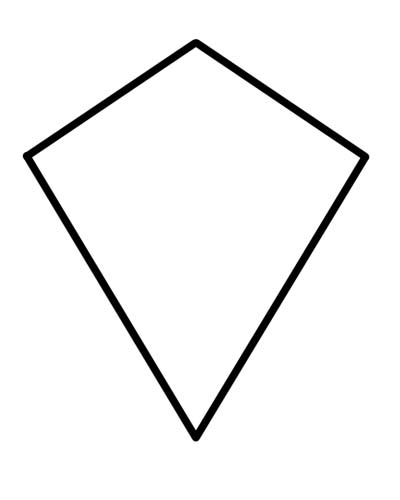
凧は、ちょうど 2 組の等しい連続する辺を持つ四辺形、または連続する辺の 2 つの互いに素な対が合同である四角形です (素な対とは、1 つの辺を両方の対で使用できないことを意味します)。
Rhombus は凧のすべての特性を満たしているため、すべての Rhombus が凧であることを知っておく必要があります。対辺が平行な凧は間違いなく菱形になります。したがって、すべてのひし形は凧ですが、その逆ではありません。凧は平行四辺形ではありません。
四角形 - 四角形は四角形と呼ばれます
平行四辺形 - 平行四辺形は、両側が平行で長さが等しい平らな形状です。
したがって、長方形、正方形、ひし形、台形、および凧の形は、それぞれ 4 つの側面があるため、四角形です。
ただし、平行四辺形は長方形、正方形、ひし形のみです。
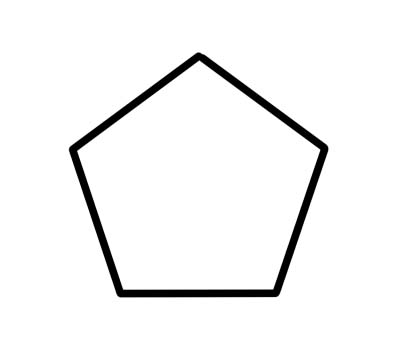
五角形は 5 つの内角を足すと 540 度になる 5 辺の多角形です。正五角形は辺の長さが等しく、各内角は 108 度です。
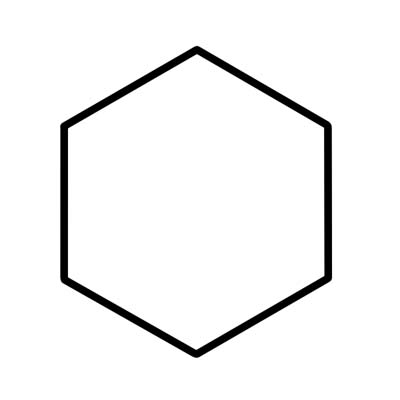
Hexagon は、720 度になる 6 つの内角を持つ 6 辺の多角形です。不規則な六角形は辺の長さが異なります。
正六角形は辺の長さが等しく、各内角は 120 度です。正六角形は、それぞれの中心角が 60 度に等しい 6 つの正三角形で構成されています。
[画像を挿入: 六角形を 6 つの三角形に分割し、中心角が 60 度の 1 つ]
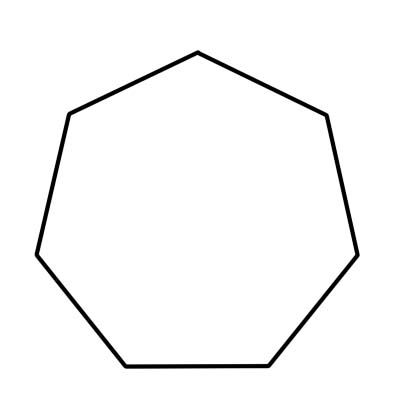
ヘプタゴンは 7 辺の多角形です。 7 つの側面に加えて、7 角形には 7 つの頂点と角度があります。 7 つの内角をすべて足すと 900 度になります。正七角形の各内角の測定値は、約 128.57 度または約 129 度です。
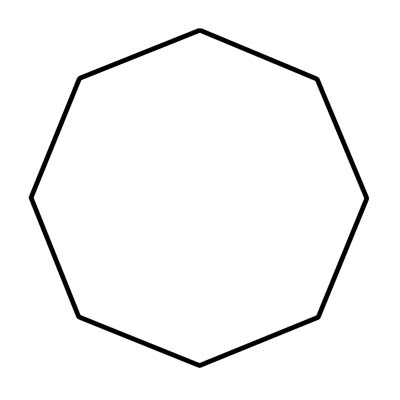
八角形は、8 つの辺と 8 つの角を含む幾何学的形状です。八角形には、接続する直線の辺が必要です。曲げたり、切り離したりすることはできません。一時停止の標識の形をした八角形を実際に目にすることがよくあります。正八角形の 8 つの内角のそれぞれの測定値は、約 108 度です。凸八角形には、内側を指す角度はありません。より正確には、内角は 180° を超えることはできません。任意の内角が 180° より大きい場合、それは凹面です
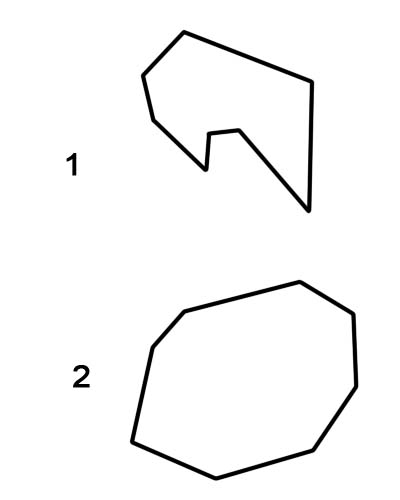
1.凹八角形
2.凸八角形
規則的な八角形は常に凸型の八角形として分類されますが、不規則な八角形は凹型または凸型のいずれかに分類されることに注意することが重要です。
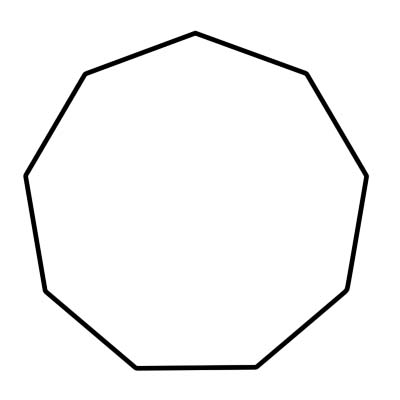
九角形は、1260 度になる 9 つの辺と 9 つの内角を持つ多角形です。正九角形はすべての辺の長さが同じで、内角の大きさもすべて同じです。正九角形の角度の測定値は 140 度です。九角形は、各中心角が 40 度に等しい 9 つの三角形で構成されます。
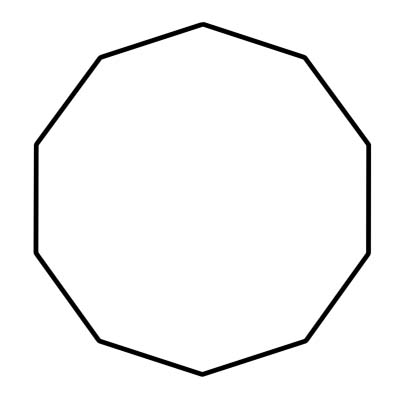
十角形は 10 角形です。また、10 個の頂点 (側面が交わる場所) と角度もあります。十角形の内角の和は1440度です。正十角形は、辺と角が一致しています。各角度は 144 度です。十角形は、中心角が 36 度に等しい 10 個の三角形で構成されます。
3 方向から測定できる形状を 3 次元形状または 3D 形状と呼びます。 3D 形状はソリッド形状とも呼ばれます。 3D 形状の 3 つの測定値は、長さ、幅、高さ (または深さまたは厚さ) です。
3D 形状は、厚みがあるため、2D 形状とは異なります。私たちの日常生活における 3D 形状の例を次に示します。
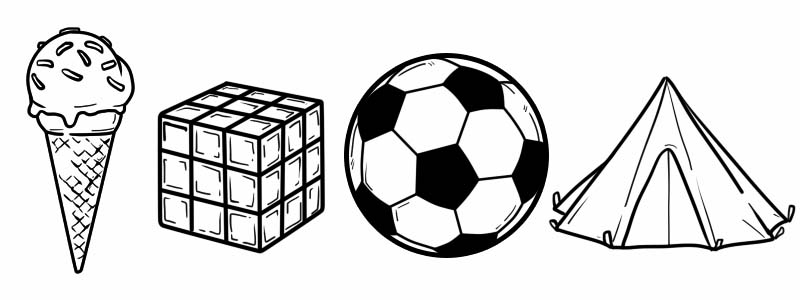
3 次元形状には、頂点、面、エッジがあります。
プリズムは、側面が平らな 3 次元 (3D) 形状の一種です。同じ形状とサイズの 2 つの端があります (2D 形状のように見えます)。端から端までの形状に沿って同じ断面を持っています。つまり、それを切り取ると、両側と同じ 2D 形状が表示されます。
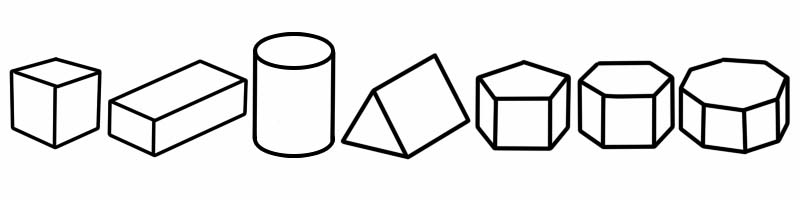
立体形状 | エッジ数 | 顔の数 | 頂点数 |
キューブ | 12 | 6 | 8 |
直方体 | 12 | 6 | 8 |
シリンダー | 2 | 3 | 0 |
三角柱 | 9 | 5 (三角形 2 個、長方形 3 個) | 6 |
五角柱 | 15 | 7 | 10 |
六角柱 | 18 | 8 | 12 |
八角柱 | 24 | 10 | 16 |
ピラミッドも 3 次元 (3D) 形状です。多角形の底面と平らな (三角形の) 側面が共通の点 (頂点と呼ばれます) で結合します。 「ピラミッド」と聞いて真っ先に思い浮かぶのは、有名なエジプトのピラミッドです。エジプトのピラミッドは正方形ベースのピラミッドですが、他にもいくつかのタイプのピラミッドがあり、それぞれが異なる多角形をベースとしています。
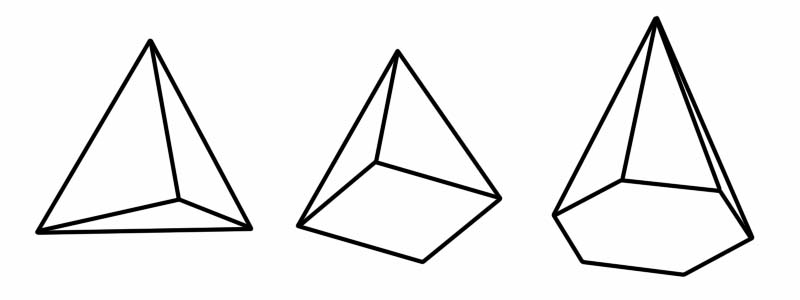
形 | エッジ数 | 顔の数 | 頂点数 |
四面体 | 6 | 4 | 4 |
四角錐 | 8 | 5 | 5 |
六角錐 | 12 | 7 | 7 |
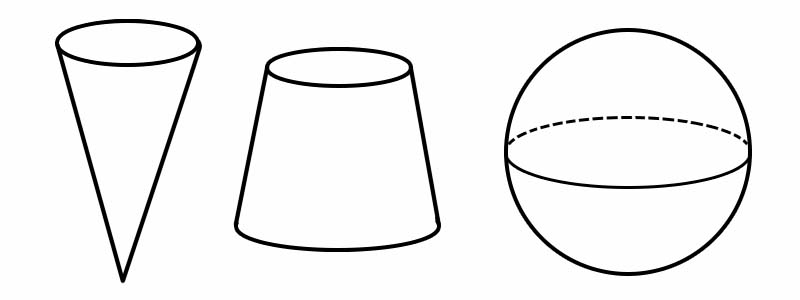
形 | エッジ数 | 顔の数 | 頂点数 |
円錐 | 1 | 2 | 1 |
錐台 | 2 | 3 | 0 |
球 | 0 | 1 | 0 |