Таны эргэн тойронд байгаа янз бүрийн объектуудыг ажиглаарай. Тэд янз бүрийн хэлбэр, хэмжээтэй ирдэг. Зарим нь адилхан, зарим нь өөр. Хэдийгээр бид бүх объектын хэлбэрийг яг таг хэлж чадахгүй ч математикийн хувьд бид 2 хэмжээст дүрс, 3 хэмжээст дүрсүүдийн талаар ихэвчлэн ярьдаг. Тэдний талаар илүү ихийг олж мэдье!
2D хэлбэр гэдэг үг нь "хоёр хэмжээст" дүрсийг илэрхийлдэг. Зөвхөн урт ба өргөн гэсэн хоёр хэмжээс бүхий геометрийн дүрс нь 2D дүрс юм. Хоёр хэмжээст дүрс нь зузаангүй. Хажуу тал нь шулуун эсвэл муруй шугамаар хийгдсэн байдаг. Тэд хэдэн ч талтай байж болно.
Хоёр хэмжээсийн тухай ойлголтыг хүн хаана ч хөдөлж болох хавтгай гадаргуу гэж ойлгож болно. Хавтгай гадаргууг хавтгай гэж нэрлэдэг. 2D хэлбэр нь цаасан дээр үргэлж байдаг зүйл юм. Энэ нь өндөргүй тул цаасан дээрээс унадаггүй. 2D дүрсийг хавтгай дүрс эсвэл хавтгай дүрс гэж нэрлэдэг.
2D дүрс нь талбайтай боловч эзэлхүүнгүй.
Хэлбэрийн шинж чанарыг тодорхойлох гурван чухал нэр томъёо байдаг:
Талууд - 2 хэмжээст дүрс дээр дүрс үүсгэх шугамын хэсэг.
Оройнууд - Зургийн булан.
Өнцөг - Геометрийн хувьд өнцгийг нийтлэг төгсгөлийн цэг дээр нийлсэн хоёр шугамаас үүссэн дүрс гэж тодорхойлж болно.
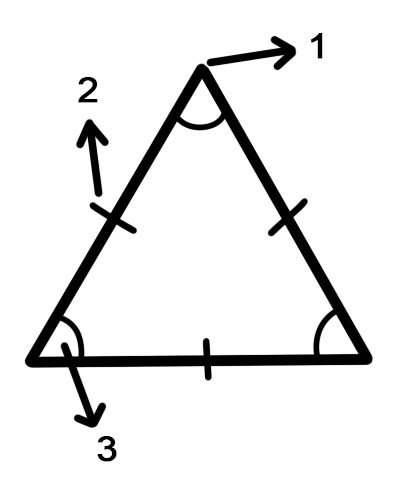
1. орой
2. талууд
3. өнцөг
Янз бүрийн 2D дүрсүүдийн талаар ярилцъя.

Тойрог нь ямар ч булан, ирмэггүй дугуй хэлбэртэй дүрс юм. Бидний эргэн тойронд бид дугуй хэлбэртэй дугуй, ханын цаг, зулзаганаас олж болно. Тойргийн төв нь тойрог дээрх цэг хүртэлх бүх зай нь тэнцүү байх тойргийн төв цэг юм. Төвөөс тойргийн аль ч цэг хүртэлх зайг радиус гэнэ. Хэрэв бид төвийг дайран өнгөрөх тойрог дээрх зайг авч үзвэл энэ нь диаметр юм. Тойрог тойрсон зайг тойргийн тойрог гэнэ.
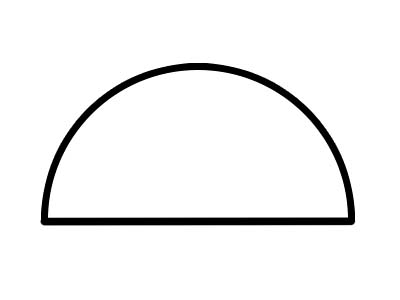
Хагас тойрог нь дээр үзүүлсэн шиг диаметртэй шугамын дагуу бүхэл бүтэн тойргийг огтолж үүссэн хагас тойрог юм. Тойргийн аль ч диаметр нь түүнийг хоёр тэнцүү хагас тойрог болгон хуваана. Хагас тойргийн бүтэн нум үргэлж 180 ° хэмжигддэг. Хэрэв жигнэмэгийг хоёр хэсэгт хуваасан бол тал бүр нь хагас тойрог болно.

Зууван нь өндөгний хэлбэр, хэлбэр, тоймтой байдаг. Зууван нь шулуун талуудгүй, булангүй боловч 1 нүүртэй байдаг бөгөөд үүнийг харахад ул мөр эсвэл хавтгай хэлбэртэй байдаг.
Олон өнцөгт нь шулуун шугам бүхий хавтгай хэлбэр юм. Жишээлбэл, гурвалжин, дөрвөн өнцөгт, таван өнцөгт, зургаан өнцөгт гэх мэт. Энгийн олон өнцөгт бүх талууд тэнцүү, бүх өнцөг нь тэнцүү байна. Үгүй бол энэ нь жигд бус олон өнцөгт болно.
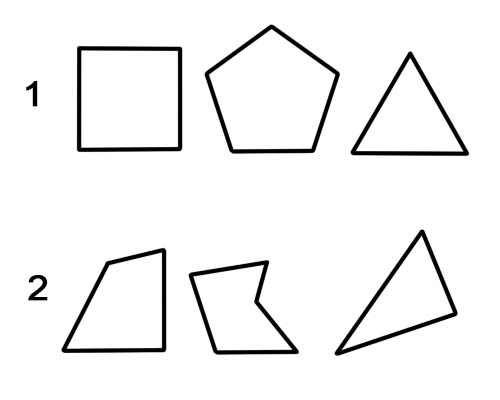
1. Энгийн олон өнцөгт.
2. Тогтмол бус олон өнцөгт.
Муруйг агуулсан тойрог ба хэлбэрүүд нь олон өнцөгт биш бөгөөд олон өнцөгт нь шулуун шугамуудаас бүрддэг.

Геометрийн хувьд гурвалжин нь гурван шулуун шугам бүхий хаалттай, хоёр хэмжээст дүрс юм. Гурвалжин бол бас олон өнцөгт юм.
Бид туг, замын хажуугийн самбар, сэндвичээс гурвалжингийн хэлбэрийг олж болно.
Гурвалжин нь гурван тал, гурван орой, гурван өнцөгтэй.
Гурвалжны гурван дотоод өнцгийн нийлбэр нь үргэлж 180° байна. Гурвалжны хоёр талын уртын нийлбэр нь гурав дахь талын уртаас үргэлж их байдаг.
Гурвалжнуудыг өнцгөөр нь ангилахын тулд бид түүний дотоод өнцөг бүрийг хэмждэг. Гурвалжинг өнцгөөр нь ангилж болно:
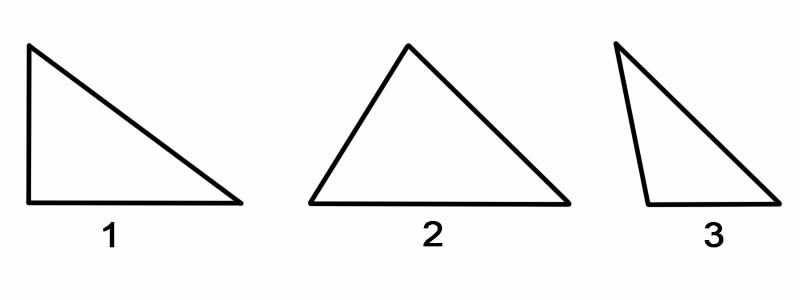
Гурвалжныг талуудын дагуу ангилахын тулд бид талуудын уртыг хэмждэг. Гурвалжнуудыг талуудаар нь ангилж болно:
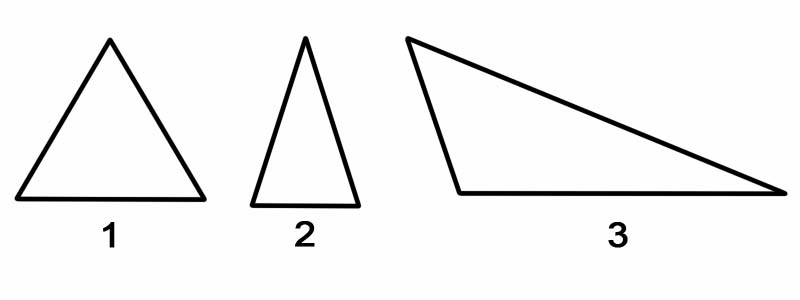
Гурвалжны чиглэлээс үл хамааран гурвалжинг үргэлж хоёр тэгш өнцөгт гурвалжинд хувааж болно гэдгийг санаарай.
Гурвалжин бол хамгийн бага талтай олон өнцөгт юм.
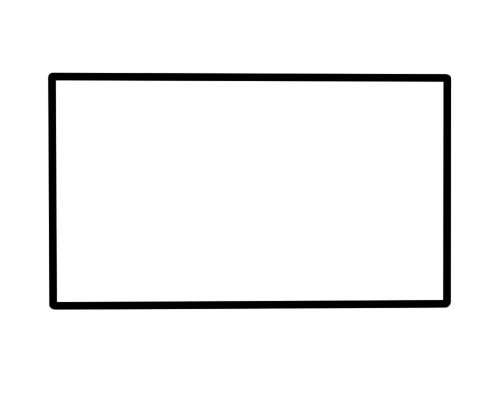
Тэгш өнцөгт нь 4 тал, 4 орой, 4 өнцөгтэй дүрс юм. Эсрэг талууд нь параллель бөгөөд уртаараа тэнцүү байна. Бүх дөрвөн өнцөг нь 90 градус байна.
Ширээ, хайрцаг, ном, хаалга, цаас нь тэгш өнцөгт шиг харагддаг.

Ромб бол 4 шулуун шугамаас үүссэн хэлбэр юм. Түүний 4 тал нь ижил урттай боловч тэгш өнцөгтөөс ялгаатай нь бүх дөрвөн өнцгийн аль нь ч 90 градус биш юм. Ромб нь алмаз шиг харагддаг. Эсрэг талууд нь параллель, эсрэг талын өнцөг нь тэнцүү байна. Ромбын хоёр диагональ нь хоорондоо перпендикуляр байна.

Квадрат нь дөрвөн тал нь ижил урттай, эсрэг талын хоёр тал нь хоорондоо параллель байдаг хоёр хэмжээст дүрс юм. Энэ нь тэгш өнцөгт ба ромбын төрөл юм (доор авч үзэх болно). Дөрвөлжингийн дотоод дөрвөн өнцөг нь 90º буюу өөрөөр хэлбэл тэдгээр нь зөв өнцөг юм. Бүх өнцгийг нэмбэл 360º болно. Дөрвөлжингийн хоёр диагональ нь ижил урттай бөгөөд тэдгээрийн огтлолцсон цэг нь квадратын төв юм.
Санаж байгаарай: Дөрвөлжин бол үргэлж ромб байдаг, харин ромбо нь үргэлж дөрвөлжин байдаггүй. Хэрэв ромбын өнцөг бүр 90o байвал дөрвөлжин болно.
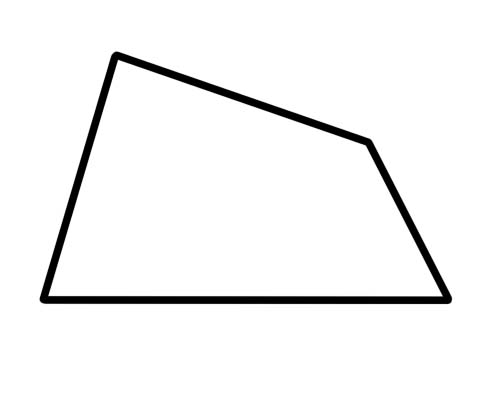
Трапец бол зөвхөн хоёр тал нь параллель байдаг дөрвөн өнцөгт юм.
Ингээд л болоо. Талууд нь тэнцүү (эсвэл тэнцүү) байх шаардлагагүй, өнцөг нь хоорондоо тохирч байх шаардлагагүй. Диагональ дээр онцгой зүйл тохиолддоггүй. Трапецын тусгай төрөл нь ижил урттай эсрэг талуудтай, ижил хэмжигдэхүүнтэй эсрэг өнцөгтэй "исс өнцөгт трапец" юм. Диагональууд нь мөн адил урттай байна.
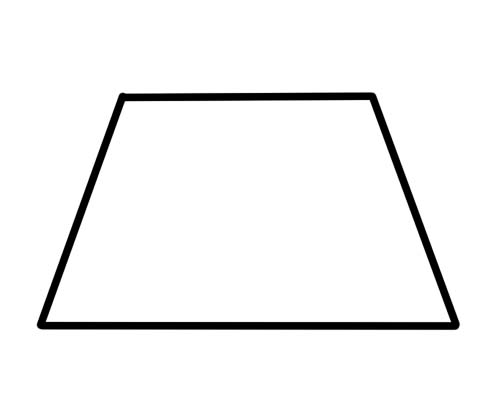
Хоёр талт гурвалжинд хажуугийн хажуугийн өнцөгүүд (бие биенийхээ хажуугийн өнцөг) нэмэлт болно. Энэ нь тэд 180 градус хүртэл нэмдэг гэсэн үг юм.
Зөвхөн нэг хос эсрэг тал нь параллель байдаг тул трапец нь параллелограмм биш юм.
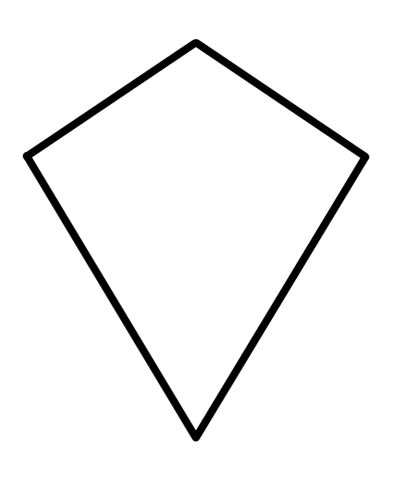
Цаасан шувуу гэдэг нь яг хоёр хос дараалсан тэгш талтай, эсвэл хоёр салангид хос дараалсан тал нь таарч байгаа дөрвөлжин хэлбэртэй (загалсан хос гэдэг нь нэг талыг хоёуланд нь ашиглах боломжгүй гэсэн үг).
Ромбус цаасан шувууны бүх шинж чанарыг хангадаг тул ромбус бүр цаасан шувуу гэдгийг мэдэх хэрэгтэй. Эсрэг талууд параллель байгаа цаасан шувуу нь ромб болно. Тиймээс ромбо бүр цаасан шувуу боловч эсрэгээрээ биш. Цаасан шувуу нь параллелограмм биш, учир нь эсрэг талууд нь хоорондоо параллель биш юм.
Дөрвөн өнцөгт - Дөрвөн талт дүрсийг дөрвөн өнцөгт гэж нэрлэдэг
Параллелограмм - Параллелограмм нь эсрэг тал нь параллель, урттай тэнцүү хавтгай хэлбэр юм.
Тэгэхлээр тэгш өнцөгт, дөрвөлжин, ромб, трапец, цаасан шувууны хэлбэрүүд нь тус бүр дөрвөн талтай тул дөрвөлжин хэлбэртэй байдаг.
Гэхдээ зөвхөн тэгш өнцөгт, дөрвөлжин, ромб нь параллелограмм юм.
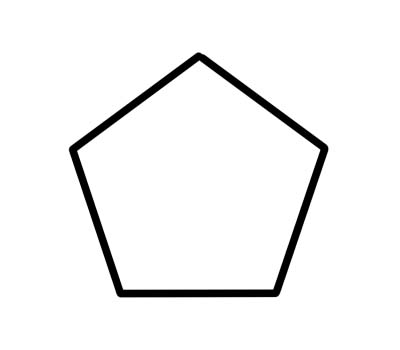
Пентагон гэдэг нь 540 градус нэмдэг таван дотоод өнцөгтэй, 5 талт олон өнцөгт юм. Энгийн таван өнцөгт нь ижил урттай талуудтай бөгөөд дотоод өнцөг бүр нь 108 градус байна.
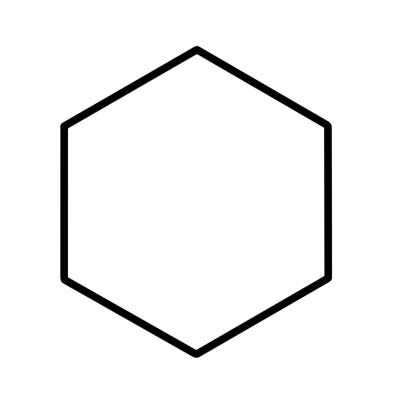
Зургаан өнцөгт нь 720 градус нэмдэг зургаан дотоод өнцөгтэй, зургаан талт олон өнцөгт юм. Тогтмол бус зургаан өнцөгт нь өөр өөр урттай талуудтай.
Ердийн зургаан өнцөгт нь ижил урттай талуудтай бөгөөд дотоод өнцөг бүр нь 120 градус байна. Ердийн зургаан өнцөгт нь төв өнцөг бүр нь 60 градустай тэнцүү зургаан тэгш талт гурвалжнаас бүрдэнэ.
[зураг оруулах: зургаан гурвалжинд хуваагдсан зургаан өнцөгт, 60 градусын нэг төв өнцөг]
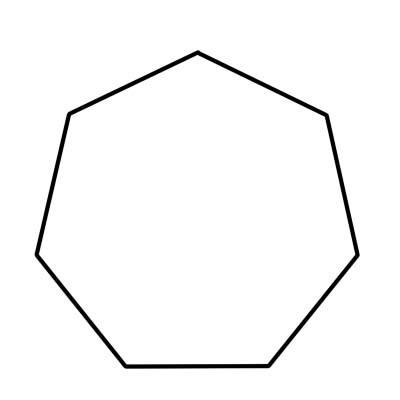
Долоон өнцөгт нь долоон талт олон өнцөгт юм. Долоон талтай хамт долоон өнцөгт долоон орой, өнцөгтэй. Долоон дотоод өнцгийг бүгдийг нь 900 хэмд нэмнэ. Ердийн долоон өнцөгтийн дотоод өнцөг бүрийн хэмжүүр нь ойролцоогоор 128.57 градус буюу ойролцоогоор 129 градус байна.
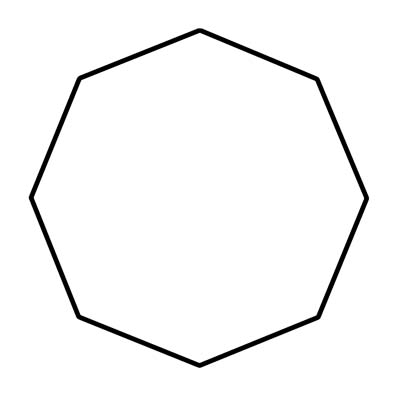
Найман өнцөгт нь найман тал, найман өнцөг агуулсан геометрийн хэлбэр юм. Найман өнцөгт нь хоорондоо холбогдсон шулуун талуудтай байх ёстой; тэдгээрийг муруй эсвэл салгах боломжгүй. Бодит амьдрал дээр та зогсолтын тэмдгийн хэлбэртэй найман өнцөгтийг олонтаа харах болно. Ердийн найман өнцөгтийн дотоод найман өнцөг бүрийн хэмжүүр нь ойролцоогоор 108 градус байна. Гүдгэр найман өнцөгт дотогшоо чиглэсэн өнцөг байхгүй. Илүү нарийн, дотоод өнцөг нь 180 ° -аас их байж болохгүй. Аливаа дотоод өнцөг нь 180 ° -аас их байвал энэ нь хотгор болно
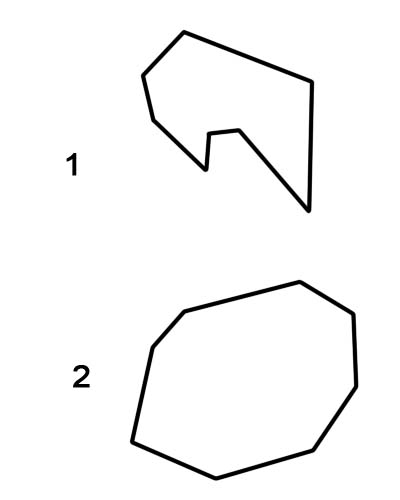
1. Хотгор найман өнцөгт
2. Гүдгэр найман өнцөгт
Энгийн найман өнцөгтийг ямагт гүдгэр найман өнцөгт гэж ангилдаг бол жигд бус найман өнцөгт нь хотгор эсвэл гүдгэр байж болно гэдгийг анхаарах нь чухал.
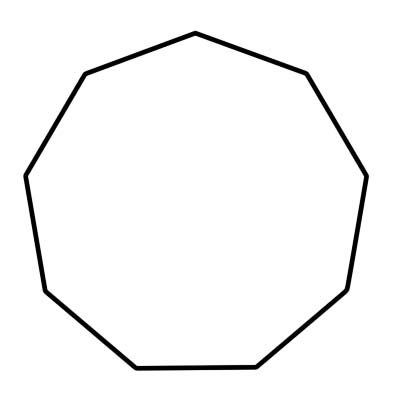
Нонагон гэдэг нь 9 тал, 9 дотоод өнцөг бүхий олон өнцөгтийг нэмээд 1260 градусаар илэрхийлдэг. Энгийн нонагон нь бүх талууд ижил урттай, бүх дотоод өнцөг нь ижил хэмжээтэй байна. Энгийн бус өнцөгтийн өнцгийн хэмжүүр нь 140 градус байна. Нонагон нь төв өнцөг бүрийн хэмжээ 40 градустай тэнцэх 9 гурвалжнаас бүрдэнэ.
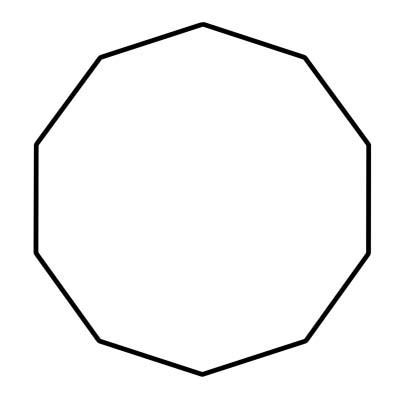
Арван өнцөгт нь 10 талт олон өнцөгт юм. Энэ нь мөн талуудын нийлдэг газар болох арван орой, өнцөгтэй. Арван өнцөгтийн дотоод өнцгийн нийлбэр нь 1440 градус байна. Тогтмол арван өнцөгт нь тэгш өнцөгт талуудтай байдаг. Өнцөг бүр нь 144 градус байна. Арван өнцөгт нь төв өнцөг нь 36 градустай тэнцэх 10 гурвалжингаас бүрдэнэ.
Гурван чиглэлд хэмжиж болох дүрсийг гурван хэмжээст дүрс буюу 3D хэлбэр гэж нэрлэдэг. 3D хэлбэрийг мөн хатуу хэлбэр гэж нэрлэдэг. 3D хэлбэрийн гурван хэмжилт нь - Урт, өргөн, өндөр (эсвэл гүн эсвэл зузаан).
3D хэлбэр нь зузаантай учраас 2D хэлбэрээс ялгаатай. Бидний өдөр тутмын амьдралын 3D хэлбэрийн зарим жишээг дурдвал:
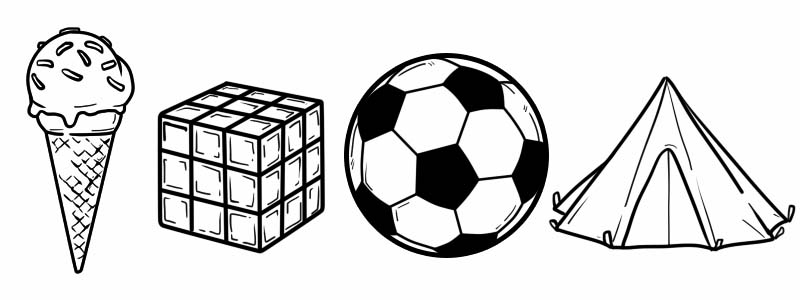
Гурван хэмжээст дүрс нь орой, нүүр, ирмэгтэй байдаг.
Призм нь хавтгай талуудтай гурван хэмжээст (3D) хэлбэрийн нэг хэлбэр юм. Энэ нь ижил хэлбэр, хэмжээтэй хоёр үзүүртэй (мөн 2 хэмжээст хэлбэртэй). Энэ нь төгсгөлөөс төгсгөл хүртэл хэлбэрийн дагуу ижил хөндлөн огтлолтой; Энэ нь хэрвээ та үүнийг огтолбол хоёр талдаа адилхан 2D дүрс харагдах болно гэсэн үг юм.
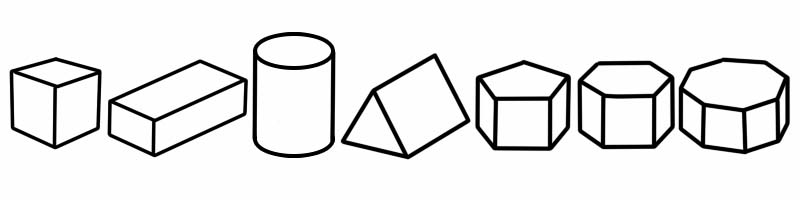
3D хэлбэр | Ирмэгүүдийн тоо | Нүүрний тоо | Оройн тоо |
Шоо | 12 | 6 | 8 |
Кубоид | 12 | 6 | 8 |
Цилиндр | 2 | 3 | 0 |
Гурвалжин призм | 9 | 5 (2 гурвалжин, 3 тэгш өнцөгт) | 6 |
Пентагональ призм | 15 | 7 | 10 |
Зургаан өнцөгт призм | 18 | 8 | 12 |
Найман өнцөгт призм | 24 | 10 | 16 |
Пирамид нь мөн гурван хэмжээст (3D) хэлбэр юм. Энэ нь олон өнцөгт суурьтай, хавтгай (гурвалжин) талуудтай бөгөөд тэдгээр нь нийтлэг цэг дээр (орой гэж нэрлэгддэг) нэгддэг. Пирамид гэдэг үгийг хэлэхэд хамгийн түрүүнд Египетийн алдарт пирамидууд санаанд буудаг. Египетийн пирамидууд нь дөрвөлжин хэлбэртэй пирамидууд боловч өөр хэд хэдэн төрлийн пирамидууд байдаг бөгөөд тус бүр нь өөр олон өнцөгт суурьтай байдаг.
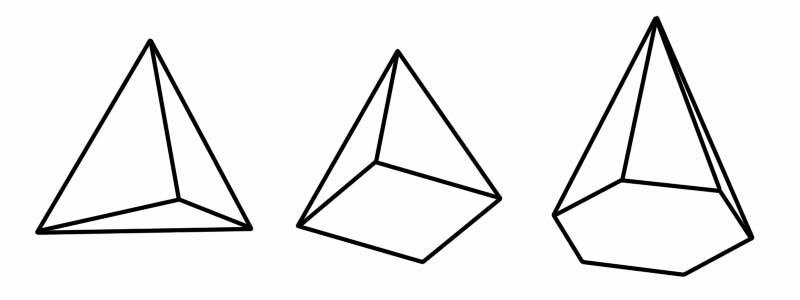
Хэлбэр | Ирмэгүүдийн тоо | Нүүрний тоо | Оройн тоо |
Тетраэдр | 6 | 4 | 4 |
Дөрвөлжин пирамид | 8 | 5 | 5 |
Зургаан өнцөгт пирамид | 12 | 7 | 7 |
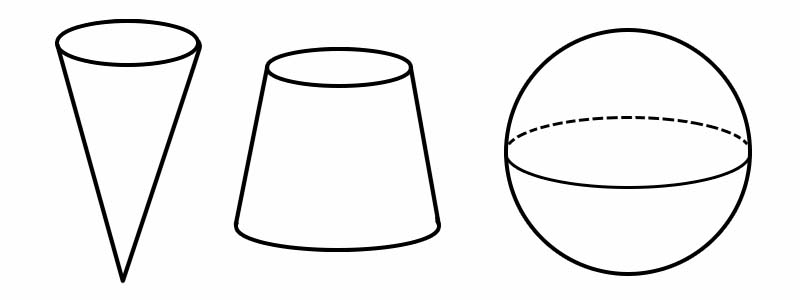
Хэлбэр | Ирмэгүүдийн тоо | Нүүрний тоо | Оройн тоо |
Конус | 1 | 2 | 1 |
Фрустум | 2 | 3 | 0 |
Бөмбөрцөг | 0 | 1 | 0 |