သင့်ပတ်ဝန်းကျင်ရှိ မတူညီသော အရာများကို ကြည့်ရှုပါ။ အမျိုးမျိုးသောပုံသဏ္ဍာန်နှင့်အရွယ်အစားအတွက်လာကြ၏။ တချို့က အတူတူပဲ၊ တချို့က မတူဘူး။ အရာဝတ္တုအားလုံး၏ ပုံသဏ္ဍာန်များကို ကျွန်ုပ်တို့ အတိအကျ အမည်မဖော်နိုင်သော်လည်း သင်္ချာတွင် 2D ပုံသဏ္ဍာန်များနှင့် 3D ပုံသဏ္ဍာန်များအကြောင်း အများစုကို ပြောဆိုကြသည်။ ၎င်းတို့အကြောင်း ပိုမိုလေ့လာကြပါစို့။
2D ပုံသဏ္ဍာန်ဟူသော စကားလုံးသည် "နှစ်ဘက်မြင်" ပုံသဏ္ဍာန်ကို ရည်ညွှန်းသည်။ အလျားနှင့် အနံသာရှိသော ဂျီဩမေတြီပုံသည် 2D ပုံသဏ္ဍာန်ဖြစ်သည်။ နှစ်ဘက်မြင် ပုံသဏ္ဍာန်များသည် အထူမရှိပါ။ ဘေးနှစ်ဖက်ကို ဖြောင့် သို့မဟုတ် မျဉ်းကြောင်းများဖြင့် ပြုလုပ်ထားသည်။ သူတို့မှာ ဘယ်ဘက်ခြမ်းရှိနိုင်တယ်။
အတိုင်းအတာနှစ်ခု၏ သဘောတရားကို မည်သည့်နေရာသို့မဆို ရွေ့လျားနိုင်သော မျက်နှာပြင်ညီညာသည်ဟု ယူဆနိုင်သည်။ ညီညာသော မျက်နှာပြင်ကို လေယာဉ်ဟု ခေါ်သည်။ 2D ပုံသဏ္ဍာန်သည် စာရွက်တစ်ရွက်ပေါ်တွင် အမြဲရှိနေသော အရာဖြစ်သည်။ ၎င်းသည် အမြင့်မရှိသောကြောင့် စာရွက်တစ်ရွက်၏အထက်တွင် ပြုတ်ကျခြင်းမရှိပါ။ 2D ပုံသဏ္ဍာန်များကို လေယာဉ်ပုံသဏ္ဍာန်များ သို့မဟုတ် လေယာဉ်ရုပ်ပုံများဟုလည်း ခေါ်သည်။
2D ပုံသဏ္ဍာန်များသည် ဧရိယာရှိသော်လည်း ထုထည်မရှိပါ။
ပုံသဏ္ဍာန်များ၏ ဝိသေသလက္ခဏာများကို ဖော်ပြရန်အတွက် အရေးကြီးသော ဝေါဟာရသုံးရပ်ရှိပါသည်။
ဘေးများ - 2 ဖက်မြင်ရုပ်ပုံပေါ်ပုံသဏ္ဍာန်တစ်ခုဖွဲ့စည်းသည့်မျဉ်းအပိုင်း။
Vertices - ပုံတစ်ခု၏ထောင့်။
ထောင့်များ - ဂျီသြမေတြီတွင် မျဉ်းနှစ်ကြောင်းဆုံသည့် ဘုံအဆုံးအမှတ်တွင် မျဉ်းနှစ်ကြောင်းဖြင့် ဖွဲ့စည်းထားသော ထောင့်ကို ထောင့်တစ်ခုဟု သတ်မှတ်နိုင်သည်။
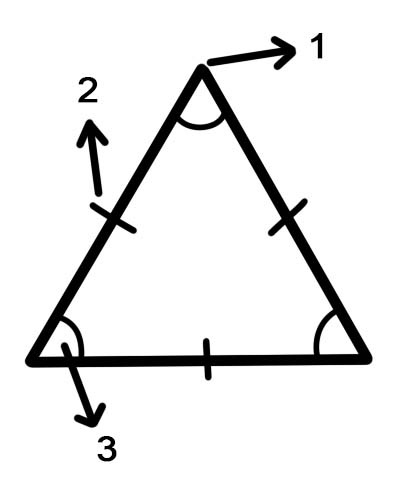
1. ထိပ်တန်း
2. ဟိုဘက်ဒီဘက်
၃။ထောင့်များ
မတူညီသော 2D ပုံသဏ္ဍာန်များကို ဆွေးနွေးကြပါစို့။

စက်ဝိုင်းသည် ထောင့် သို့မဟုတ် အစွန်းများမရှိသော အဝိုင်းပုံသဏ္ဍာန်ဖြစ်သည်။ ကားတာယာ၊ တိုင်ကပ်နာရီနှင့် lollipop တို့တွင် စက်ဝိုင်းပုံသဏ္ဍာန်ကို ကျွန်ုပ်တို့ တွေ့ရှိနိုင်သည်။ စက်ဝိုင်းတစ်ခု၏ အလယ်ဗဟိုသည် စက်ဝိုင်းတစ်ခုရှိ အလယ်ဗဟိုအချက်ဖြစ်ပြီး၊ စက်ဝိုင်းပေါ်ရှိ အမှတ်များနှင့် အကွာအဝေးအားလုံးသည် ညီမျှသည်။ အလယ်မှ စက်ဝိုင်းရှိ မည်သည့်အမှတ်သို့မဆို အကွာအဝေးကို အချင်းဝက်ဟုခေါ်သည်။ အလယ်ဗဟိုကိုဖြတ်၍ စက်ဝိုင်းကိုဖြတ်၍ အကွာအဝေးကို သုံးသပ်ပါက၊ အချင်းဖြစ်သည်။ စက်ဝိုင်းပတ်ပတ်လည်အကွာအဝေးကို စက်ဝိုင်း၏အဝန်းဟုခေါ်သည်။
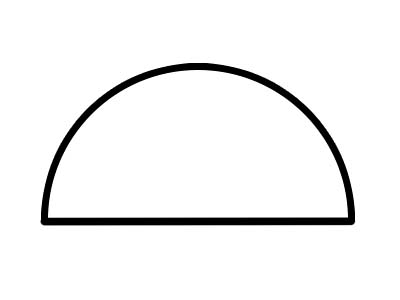
စက်ဝိုင်းခြမ်းသည် အထက်တွင်ပြထားသည့်အတိုင်း အချင်းမျဉ်းတစ်လျှောက် စက်ဝိုင်းတစ်ခုလုံးကို ဖြတ်တောက်ခြင်းဖြင့် ဖွဲ့စည်းထားသော စက်ဝိုင်းတစ်ဝက်ဖြစ်သည်။ စက်ဝိုင်းတစ်ခု၏ အချင်းသည် ၎င်းအား အညီအမျှ စက်ဝိုင်းခြမ်းနှစ်ခုဖြစ်အောင် ဖြတ်သည်။ စက်ဝိုင်းခြမ်းတစ်ခု၏ ထောင့်အပြည့်သည် 180° အမြဲတိုင်းသည်။ ကွတ်ကီးကို နှစ်ပိုင်းခွဲထားပါက တစ်ဝက်စီသည် စက်ဝိုင်းပုံဖြစ်သည်။

ဘဲဥပုံတစ်ခုတွင် ကြက်ဥ၏ပုံစံ၊ ပုံသဏ္ဍာန် သို့မဟုတ် ပုံသဏ္ဍာန်ရှိသည်။ ဘဲဥပုံတစ်ခုတွင် တည့်တည့်အစွန်းများမရှိသော်လည်း ထောင့်မရှိသော်လည်း ကြည့်သည့်အခါ ခြေရာခံနိုင် သို့မဟုတ် ခြေရာခံနိုင်သော သို့မဟုတ် မြင်နိုင်သည့်မျက်နှာတစ်ခုရှိသည်။
ဗဟုဂံတစ်ခုသည် မျဉ်းဖြောင့်များပါရှိသော လေယာဉ်ပုံသဏ္ဍာန်ဖြစ်သည်။ ဥပမာများတွင် တြိဂံများ၊ လေးထောင့်ပုံများ၊ ပင်တဂွန်များ၊ ဆဋ္ဌဂံ အစရှိသည်တို့ ပါဝင်သည်။ ပုံမှန်ပိုလီဂံတစ်ခုတွင် အဘက်အားလုံး ညီပြီး ထောင့်အားလုံး တူညီသည်။ မဟုတ်ပါက၊ ၎င်းသည် မမှန်သော polygon တစ်ခုဖြစ်သည်။
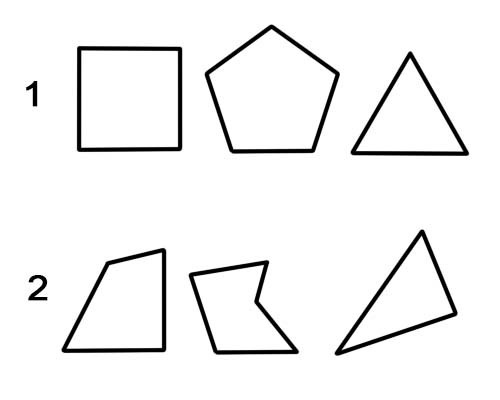
1. ပုံမှန် polygon ။
2. ပုံမမှန်သော ဗဟုဂံ။
မျဉ်းကွေးများပါ၀င်သည့် စက်ဝိုင်းများနှင့် ပုံသဏ္ဍာန်များသည် ပေါင်းကူးဂံများမဟုတ်ပါ - အဓိပ္ပါယ်အရ မျဉ်းဖြောင့်ဖြင့် ဖွဲ့စည်းထားသော ဗဟုဂံတစ်ခု။

ဂျီသြမေတြီတွင်၊ တြိဂံသည် မျဉ်းဖြောင့်သုံးကြောင်းရှိသော အပိတ်နှစ်ဖက်မြင်ပုံသဏ္ဍာန်ဖြစ်သည်။ တြိဂံသည် ဗဟုဂံတစ်ခုလည်းဖြစ်သည်။
အလံ၊ လမ်းဘေးဆိုင်းဘုတ်နှင့် အသားညှပ်ပေါင်မုန့်များတွင် တြိဂံပုံသဏ္ဍာန်ကို ကျွန်ုပ်တို့ တွေ့ရှိနိုင်သည်။
တြိဂံတစ်ခုတွင် ထောင့်သုံးဘက်၊ ဒေါင်လိုက် သုံးခုနှင့် ထောင့်သုံးထောင့်ရှိသည်။
တြိဂံတစ်ခု၏ အတွင်းထောင့်သုံးခု၏ ပေါင်းလဒ်သည် အမြဲတမ်း 180° ဖြစ်သည်။ တြိဂံတစ်ခု၏ နှစ်ဖက်အလျား၏ ပေါင်းလဒ်သည် တတိယအခြမ်း၏ အလျားထက် အမြဲပိုနေပါသည်။
၎င်းတို့၏ထောင့်များအလိုက် တြိဂံများကို အမျိုးအစားခွဲရန်၊ ၎င်း၏အတွင်းထောင့်တစ်ခုစီကို ကျွန်ုပ်တို့တိုင်းတာသည်။ တြိဂံများကို ထောင့်များဖြင့် ခွဲခြားနိုင်သည်-
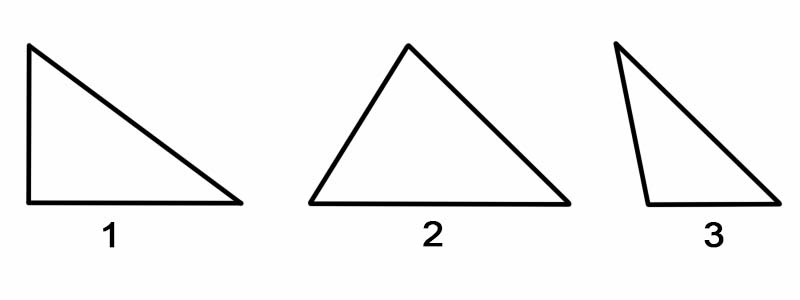
တြိဂံများကို ၎င်းတို့၏ အစွန်းများအလိုက် အမျိုးအစားခွဲရန်၊ ၎င်း၏ အစွန်းတစ်ဖက်စီ၏ အလျားကို တိုင်းတာသည်။ တြိဂံများကို ၎င်းတို့၏ နှစ်ဖက်ဖြင့် ခွဲခြားနိုင်သည်-
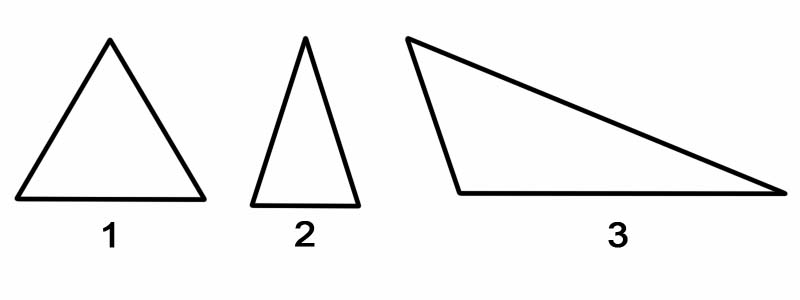
သတိရပါ- တြိဂံတစ်ခုသည် ၎င်း၏ ဦးတည်ချက်မမူဘဲ ညာဘက်တြိဂံနှစ်ခုသို့ အမြဲတမ်းကွဲနိုင်သည်။
တြိဂံများသည် နှစ်ဖက်အရေအတွက် အနည်းဆုံးပါရှိသော ထောင့်များဖြစ်သည်။
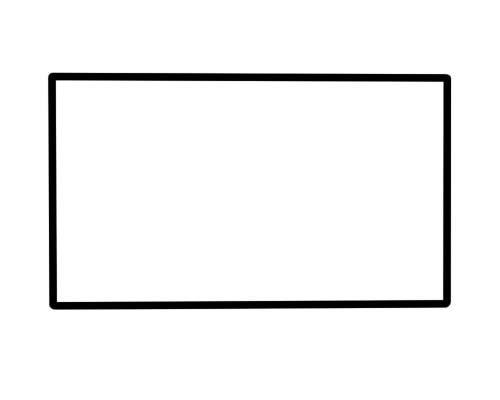
ထောင့်မှန်စတုဂံသည် အဘက် ၄ ဘက်၊ ထောင့် ၄ ထောင့်နှင့် ထောင့် ၄ ခုပါရှိသော ပုံသဏ္ဍာန်တစ်ခုဖြစ်သည်။ ဆန့်ကျင်ဘက်အခြမ်းများသည် မျဉ်းပြိုင်ဖြစ်ပြီး အလျားတူညီသည်။ ထောင့်(၄)ခုစလုံးသည် ၉၀ဒီဂရီတိုင်းတာသည်။
စားပွဲများ၊ သေတ္တာများ၊ စာအုပ်များ၊ တံခါးများနှင့် စက္ကူများသည် စတုဂံပုံသဏ္ဍာန်တူသည်။

တောင်ဥပုံသည် မျဉ်းဖြောင့် ၄ ကြောင်းဖြင့် ဖွဲ့စည်းထားသော ပုံသဏ္ဍာန်ဖြစ်သည်။ ၎င်း၏အလျား 4 ထောင့်သည် တူညီသော်လည်း ထောင့်မှန်စတုဂံနှင့်မတူဘဲ ထောင့် 4 ထောင့်တစ်ခုမှ 90 ဒီဂရီမတိုင်းတာပါ။ တောင်ဥပုံသည် စိန်နှင့်တူသည်။ ဆန့်ကျင်ဘက်အခြမ်းများသည် မျဉ်းပြိုင်ဖြစ်ပြီး ဆန့်ကျင်ဘက်ထောင့်များသည် ညီမျှသည်။ တောင်ဥပုံ၏ ထောင့်ဖြတ်နှစ်ခုသည် တစ်ခုနှင့်တစ်ခု ထောင့်ဖြတ်ထားသည်။

စတုရန်းတစ်ခုသည် အလျားလေးဖက်စလုံး ညီတူညီမျှရှိသော နှစ်ဘက်မြင်ရုပ်ပုံဖြစ်ပြီး ဆန့်ကျင်ဘက်နှစ်ဖက်သည် တစ်ခုနှင့်တစ်ခု အပြိုင်ဖြစ်သည်။ ၎င်းသည် ထောင့်မှန်စတုဂံနှင့် တောင်ပုံးပုံ အမျိုးအစား (အောက်တွင် ဆွေးနွေးထားသည်)။ စတုရန်းတစ်ခု၏ အတွင်းထောင့် 4 ခုသည် 90º သို့မဟုတ် တစ်နည်းအားဖြင့် ၎င်းတို့သည် ထောင့်မှန်များဖြစ်သည်။ ထောင့်အားလုံးကို ပေါင်းလိုက်သောအခါ၊ ၎င်းတို့သည် 360º အထိ ပေါင်းထည့်သည်။ စတုရန်းတစ်ခုပါရှိသော ထောင့်ဖြတ်နှစ်ခုသည် အလျားတူညီပြီး ၎င်းတို့ဖြတ်သွားသောအချက်သည် စတုရန်း၏ဗဟိုဖြစ်သည်။
သတိရပါ- စတုရန်းတစ်ခုသည် အမြဲလိုလို တောင်ဥပုံတစ်ပုံဖြစ်သော်လည်း တောင် rhombus သည် အမြဲတမ်းစတုရန်းတစ်ခုမဟုတ်ပေ။ Rumbus ၏ထောင့်တစ်ခုစီသည် 90o ဖြစ်ပါက၊ ၎င်းသည် စတုရန်းတစ်ခုဖြစ်သည်။
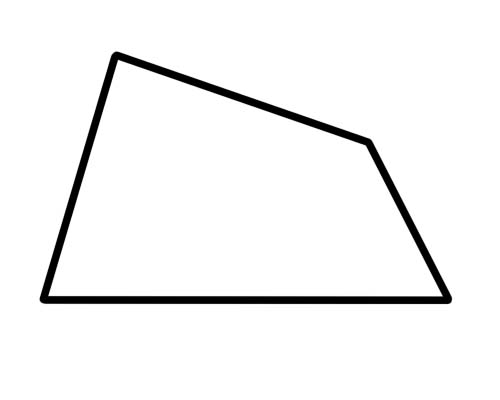
Trapezium သည် အပြိုင်နှစ်ဘက်သာရှိသော လေးထောင့်ပုံစံဖြစ်သည်။
ဒါပဲ။ ဘယ်ဖက်ကမှ ညီညွှတ်မှု (သို့မဟုတ်) တန်းတူဖြစ်ရန် မလိုအပ်သလို ထောင့်များ လိုက်လျောညီထွေရှိရန် မလိုအပ်ပါ။ ထောင့်ဖြတ်တွေနဲ့တော့ ဘာမှထူးထူးခြားခြားမဖြစ်ပါဘူး။ ကုပ်ပိုးအမျိုးအစား အထူးအမျိုးအစားမှာ တူညီသောအတိုင်းအတာ၏ အရှည်နှင့် ဆန့်ကျင်ဘက်ထောင့်များရှိသည့် 'isosceles trapezium' ဖြစ်သည်။ ထောင့်ဖြတ်များသည်လည်း အလျား တူညီကြသည်။
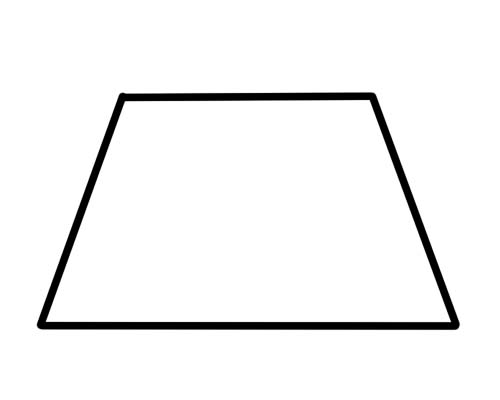
isosceles တြိဂံတစ်ခုတွင်၊ ဘေးနှစ်ဖက်တစ်လျှောက် ကပ်လျက်ထောင့်များ (တစ်ခုနှင့်တစ်ခုဘေးရှိထောင့်များ) သည် ဖြည့်စွက်ဖြစ်သည်။ ဆိုလိုသည်မှာ ၎င်းတို့သည် 180 ဒီဂရီအထိ ပေါင်းထည့်သည်။
Trapezium သည် မျဉ်းပြိုင်တစ်ခုမဟုတ်ပါ။
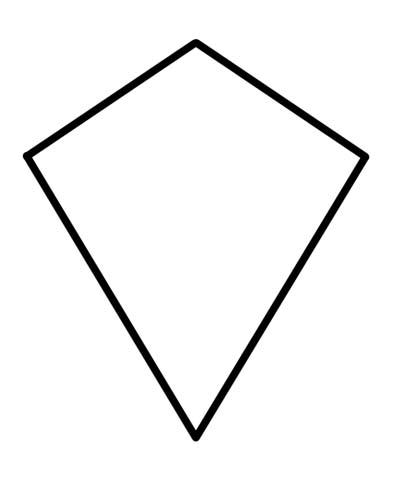
စွန်တစ်ကောင်သည် တစ်ဆက်တည်း တူညီသော တစ်ဖက်မှ အတွဲနှစ်စုံတိတိ ရှိသော လေးထောင့်ပုံ သို့မဟုတ် အဆက်အစပ် နှစ်ခု ဆက်တိုက် ညီနေ သော လေးထောင့်ပုံ (disjoint pairs ဆိုသည်မှာ တစ်ဖက်ကို အတွဲ နှစ်ခုလုံးတွင် အသုံးမပြုနိုင်)။
Rhombus သည် စွန်ရဲ၏ ဂုဏ်သတ္တိအားလုံးကို ဖြည့်ဆည်းပေးသောကြောင့် Rhombus တိုင်းသည် စွန်တစ်ကောင်ဖြစ်ကြောင်း သင်သိထားရန်လိုအပ်ပါသည်။ စွန်သည် တစ်ဖက်နှင့်တစ်ဖက် အပြိုင်ဖြစ်နေသည်မှာ သေချာပါသည်။ ထို့ကြောင့် Rhombus တိုင်းသည် စွန်တစ်ကောင်ဖြစ်သော်လည်း အပြန်အလှန်မဟုတ်ပေ။ စွန်သည် မျဉ်းပြိုင်မဟုတ်သောကြောင့် တစ်ဖက်နှင့်တစ်ဖက် အပြိုင်မဟုတ်ပေ။
Quadrilaterals - လေးဘက်ခြမ်းပုံအား လေးထောင့်ပုံသဏ္ဍာန်ဟုခေါ်သည်။
Parallelogram - မျဉ်းပြိုင်တစ်ခုသည် တစ်ဖက်နှင့်တစ်ဖက် အပြိုင်အလျားနှင့် တူညီသော မျဉ်းပြိုင်ပုံစံဖြစ်သည်။
ထို့ကြောင့်၊ စတုဂံ၊ စတုရန်းပုံ၊ တောင်ပုံးပုံ၊ ကုပ်ပိုးနှင့် စွန်ပုံများသည် လေးဘက်စီတွင် လေးဘက်စီရှိသောကြောင့် လေးထောင့်ပုံသဏ္ဍာန်များဖြစ်သည်။
သို့သော်၊ စတုဂံ၊ စတုရန်းနှင့် တောင်ဥရုပ်များသည် အပြိုင်များသာဖြစ်သည်။
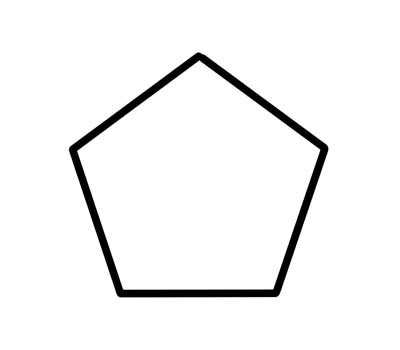
Pentagon သည် 540 ဒီဂရီအထိ ပေါင်းထည့်နိုင်သော အတွင်းထောင့်ငါးခုပါသည့် 5 ဘက်ရှိ ပေါ်လီဂွန်တစ်ခုဖြစ်သည်။ ပုံမှန် pentagons များသည် တူညီသော အလျားများရှိပြီး အတွင်းထောင့်တစ်ခုစီသည် 108 ဒီဂရီဖြစ်သည်။
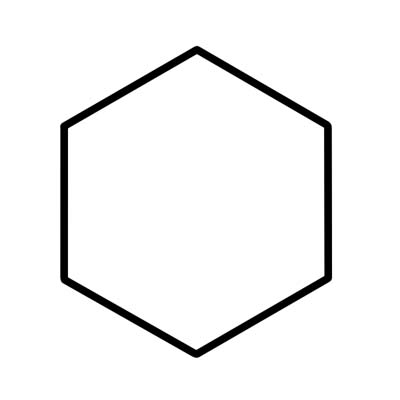
Hexagon သည် 720 ဒီဂရီအထိ ပေါင်းထည့်နိုင်သော အတွင်းထောင့်ခြောက်ခုပါသော 6-ဘက်ရှိ polygon တစ်ခုဖြစ်သည်။ ပုံမမှန်သော ဆဋ္ဌဂံများသည် အရှည်အမျိုးမျိုးရှိသည်။
ပုံမှန် ဆဋ္ဌဂံတစ်ခုသည် တူညီသောအလျားနှစ်ဖက်ရှိပြီး အတွင်းထောင့်တစ်ခုစီသည် 120 ဒီဂရီဖြစ်သည်။ ပုံမှန် ဆဋ္ဌဂံကို ဗဟိုထောင့်တစ်ခုစီသည် ၆၀ ဒီဂရီ ညီမျှသော တြိဂံခြောက်ခုဖြင့် ဖွဲ့စည်းထားသည်။
[ပုံထည့်သွင်းခြင်း- ဆဋ္ဌဂံကို တြိဂံခြောက်ခုအဖြစ် ပိုင်းခြားထားပြီး 60 ဒီဂရီ တိုင်းတာသည့် ဗဟိုထောင့်တစ်ခု]
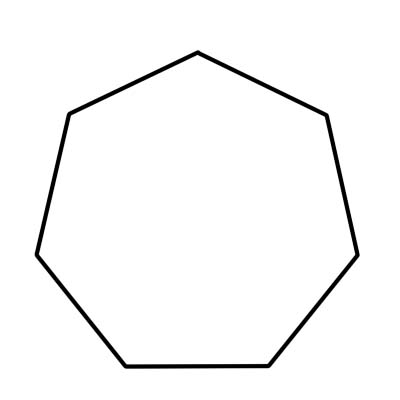
heptagon သည် ခုနစ်ဘက်စလုံး polygon ဖြစ်သည်။ ထောင့်ခုနစ်ဘက်နှင့် ထောင့်စွန်းခုနစ်ခုပါရှိသည်။ အတွင်းထောင့် ခုနစ်ခုစလုံးကို ၉၀၀ ဒီဂရီအထိ ပေါင်းထည့်သည်။ ပုံမှန် heptagon ၏ အတွင်းထောင့်တစ်ခုစီ၏ အတိုင်းအတာသည် 128.57 ဒီဂရီ သို့မဟုတ် 129 ဒီဂရီခန့်ဖြစ်သည်။
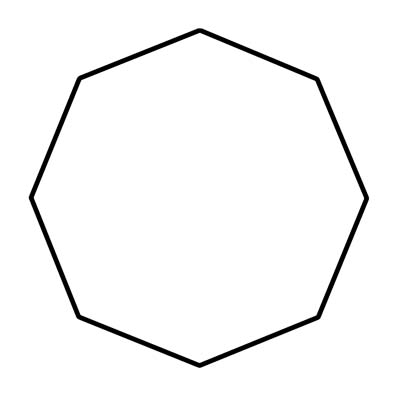
အဋ္ဌဂံတစ်ခုသည် ထောင့်ရှစ်ထောင့်နှင့် ထောင့်ရှစ်ခုပါရှိသော ဂျီဩမေတြီပုံသဏ္ဍာန်ဖြစ်သည်။ အဋ္ဌဂံများသည် တည့်တည့်ချိတ်ဆက်သော နှစ်ဖက်ရှိရမည်။ ၎င်းတို့သည် ကွေးနိုင် သို့မဟုတ် အဆက်ဖြတ်၍ မရပါ။ ရပ်တန့်သင်္ကေတပုံသဏ္ဍာန်ဖြင့် လက်တွေ့ဘဝတွင် octagons များကို မကြာခဏတွေ့ရပါမည်။ ပုံမှန်အဋ္ဌဂံတစ်ခုစီ၏ အတွင်းထောင့်ရှစ်ခုစီ၏ အတိုင်းအတာသည် ၁၀၈ ဒီဂရီခန့်ဖြစ်သည်။ အဋ္ဌဂံခုံးတစ်ခုသည် အတွင်းဘက်သို့ညွှန်ပြသောထောင့်များ မရှိပါ။ ပို၍တိကျသည်မှာ၊ အတွင်းထောင့်များသည် 180° ထက်ပို၍မရနိုင်ပါ။ အတွင်းထောင့်သည် 180° ထက်ကြီးသောအခါ၊ ၎င်းသည် ခုံးနေပါသည်။
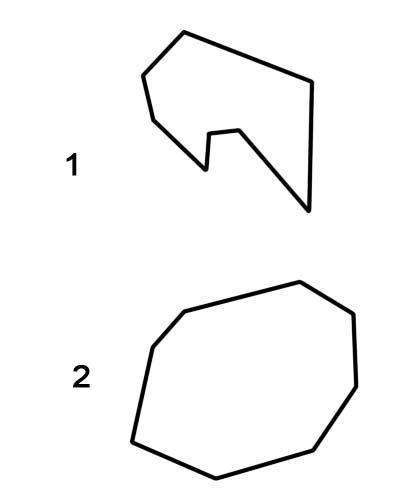
1. Concave အဋ္ဌဂံ
2. အဋ္ဌဂံခုံး
ပုံမှန် octagon များကို convex octagons အဖြစ် အမြဲတမ်း ခွဲခြားထားရန် အရေးကြီးပြီး မမှန်သော octagon များသည် concave သို့မဟုတ် convex ဖြစ်နိုင်ပါသည်။
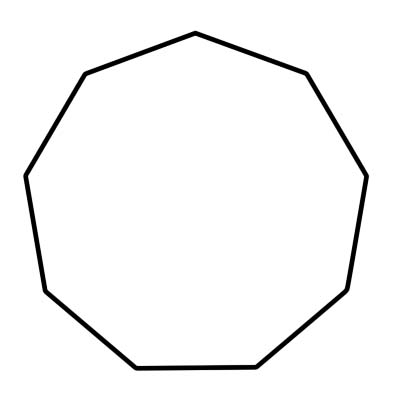
nonagon သည် 1260 ဒီဂရီအထိ ပေါင်းထည့်နိုင်သော အတွင်းထောင့် 9 ခုနှင့် အတွင်းထောင့် 9 ခုပါရှိသော polygon တစ်ခုဖြစ်သည်။ ပုံမှန် nonagon တစ်ခုတွင် အလျားတူညီပြီး အတွင်းထောင့်အားလုံးသည် အရွယ်အစားတူညီပါသည်။ ပုံမှန် nonagon ၏ ထောင့်သည် 140 ဒီဂရီ ဖြစ်သည်။ နိုဂွန်ကို တြိဂံ ၉ ခုဖြင့် ဖွဲ့စည်းထားပြီး ဗဟိုထောင့်တစ်ခုစီ၏ အတိုင်းအတာသည် ၄၀ ဒီဂရီ ညီမျှသည်။
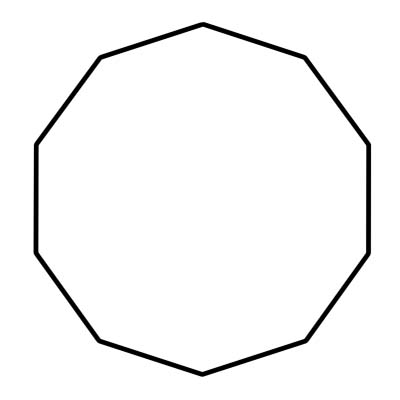
decagon တစ်ခုသည် 10-sided polygon တစ်ခုဖြစ်သည်။ ၎င်းတွင် နှစ်ဖက်ဆုံသည့် ထောင့်များနှင့် ထောင့်ဆယ်ခုလည်း ပါရှိသည်။ decagon တစ်ခု၏အတွင်းပိုင်းထောင့်ပေါင်းစုသည် 1440 ဒီဂရီဖြစ်သည်။ ပုံမှန် decagon တစ်ခုတွင် အချိုးညီသော ဘေးများနှင့် ထောင့်များရှိသည်။ ထောင့်တစ်ခုစီတိုင်းသည် 144 ဒီဂရီဖြစ်သည်။ decagon တစ်ခုကို ဗဟိုထောင့် ၃၆ ဒီဂရီနှင့် ညီမျှသော တြိဂံ ၁၀ ခုဖြင့် ပြုလုပ်ထားသည်။
သုံးဖက်မြင် ပုံသဏ္ဍာန်များ သို့မဟုတ် 3D ပုံသဏ္ဍာန်များဟု ခေါ်သည်။ 3D ပုံသဏ္ဍာန်များကို အစိုင်အခဲပုံသဏ္ဍာန်ဟုလည်း ခေါ်သည်။ 3D ပုံသဏ္ဍာန်များ၏ တိုင်းတာမှုသုံးမျိုးမှာ - အလျား၊ အနံနှင့် အမြင့် (သို့မဟုတ် အတိမ်အနက် သို့မဟုတ် အထူ) ဖြစ်သည်။
အထူရှိသောကြောင့် 3D ပုံသဏ္ဍာန်များသည် 2D ပုံသဏ္ဍာန်များနှင့် ကွဲပြားပါသည်။ ကျွန်ုပ်တို့၏နေ့စဉ်ဘဝမှ 3D ပုံသဏ္ဍာန်အချို့ ဥပမာများမှာ-
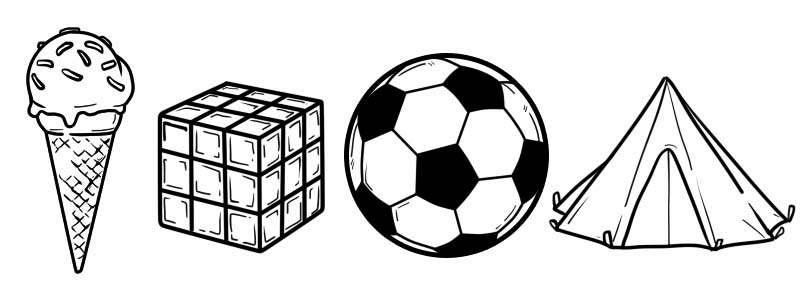
သုံးဖက်မြင်ပုံသဏ္ဍာန်များသည် ဒေါင်လိုက်များ၊ မျက်နှာများနှင့် အစွန်းများရှိသည်။
ပရစ်ဇမ်သည် ပြားချပ်ချပ်ချပ်များရှိသော သုံးဖက်မြင် (3D) ပုံသဏ္ဍာန် အမျိုးအစားဖြစ်သည်။ ၎င်းတွင် တူညီသော ပုံသဏ္ဍာန်နှင့် အရွယ်အစား (2D ပုံသဏ္ဍာန်ကဲ့သို့) အစွန်းနှစ်ခုရှိသည်။ ၎င်းသည် အဆုံးမှ အဆုံး ပုံသဏ္ဍာန်နှင့်အတူ တူညီသော အပိုင်းများပါရှိသည်။ ဆိုလိုသည်မှာ ၎င်းကိုဖြတ်လိုက်လျှင် တစ်ဖက်တစ်ချက်စီတွင် တူညီသော 2D ပုံသဏ္ဍာန်ကို မြင်တွေ့ရမည်ဖြစ်သည်။
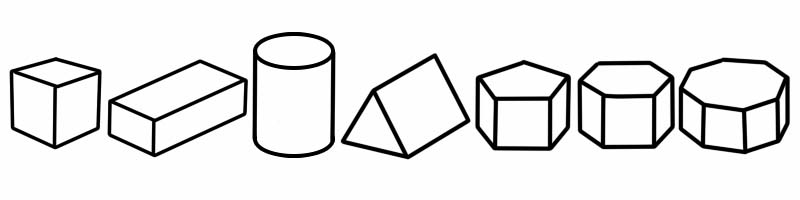
3D ပုံသဏ္ဍာန် | အနားအရေအတွက် | မျက်နှာအရေအတွက် | ဒေါင်လိုက် အရေအတွက် |
Cube | ၁၂ | ၆ | ၈ |
Cuboid | ၁၂ | ၆ | ၈ |
ဆလင်ဒါ | ၂ | ၃ | ၀ယ်တယ်။ |
တြိဂံပရစ်ဇမ် | ၉ | ၅ (တြိဂံ ၂ ခု၊ စတုဂံ ၃ ခု) | ၆ |
Pentagonal prism | ၁၅ | ၇ | ၁၀ |
ဆဋ္ဌဂံ ပရစ်ဇမ် | ၁၈ | ၈ | ၁၂ |
အဋ္ဌဂံ ပရစ်ဇမ် | ၂၄ | ၁၀ | ၁၆ |
ပိရမစ်သည် သုံးဖက်မြင် (3D) ပုံသဏ္ဍာန်လည်း ဖြစ်သည်။ ၎င်းတွင် ဘုံပွိုင့် (အထွတ်ဟုခေါ်သည်) တွင် ပေါင်းထားသော မျဉ်းကြောင်းနှင့် အပြား (တြိဂံ) နှစ်ဖက်ရှိသည်။ 'ပိရမစ်' ဟူသော စကားလုံးကို ဖော်ပြသောအခါ၊ ကျွန်ုပ်တို့ စိတ်ထဲတွင် ပထမဆုံးပေါ်လာသည်မှာ အီဂျစ်နိုင်ငံ၏ ထင်ရှားသော ပိရမစ်များဖြစ်သည်။ အီဂျစ်ပိရမစ်များသည် စတုရန်းပုံအခြေခံ ပိရမစ်များဖြစ်သော်လည်း၊ တစ်ခုစီသည် ၎င်း၏အခြေခံအဖြစ် ကွဲပြားသော polygon ပါရှိသည့် အခြားပိရမစ်အမျိုးအစားများစွာရှိသည်။
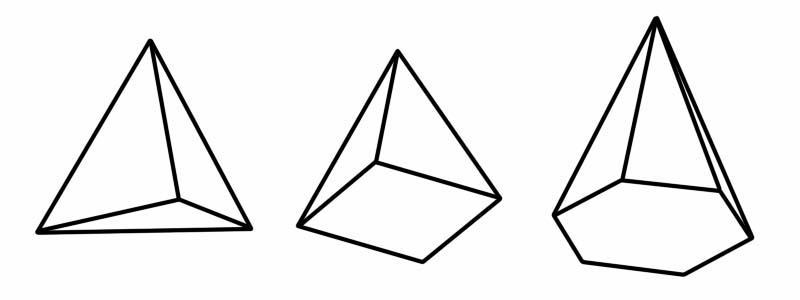
ပုံသဏ္ဍာန် | အနားအရေအတွက် | မျက်နှာအရေအတွက် | ဒေါင်လိုက် အရေအတွက် |
Tetrahedron | ၆ | ၄ | ၄ |
စတုရန်းပိရမစ် | ၈ | ၅ | ၅ |
ဆဋ္ဌဂံပိရမစ် | ၁၂ | ၇ | ၇ |
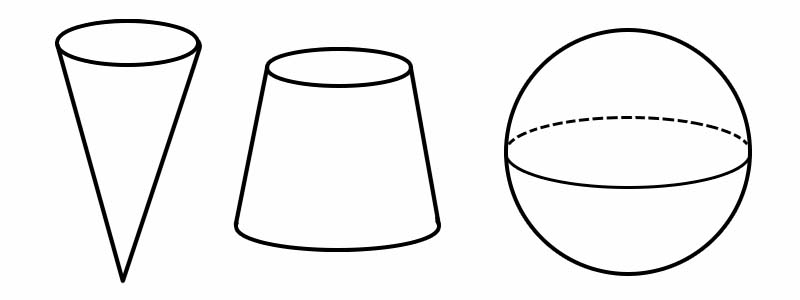
ပုံသဏ္ဍာန် | အနားအရေအတွက် | မျက်နှာအရေအတွက် | ဒေါင်လိုက် အရေအတွက် |
ပုံး | ၁ | ၂ | ၁ |
စိတ်မပူပါနဲ့။ | ၂ | ၃ | ၀ယ်တယ်။ |
စက်လုံး | ၀ယ်တယ်။ | ၁ | ၀ယ်တယ်။ |