आफ्नो वरपरका विभिन्न वस्तुहरू अवलोकन गर्नुहोस्। तिनीहरू विभिन्न आकार र आकारहरूमा आउँछन्। कोही उस्तै र कोही फरक छन् । यद्यपि हामी सबै वस्तुहरूको आकारहरू ठीकसँग नाम गर्न सक्दैनौं, गणितमा हामी ठूलो मात्रामा 2D आकारहरू र 3D आकारहरूको बारेमा कुरा गर्छौं। तिनीहरूको बारेमा थप जानौं!
शब्द 2D आकारले "दुई-आयामी" आकारलाई बुझाउँछ। एउटा ज्यामितीय आकृति जसमा दुई आयामहरू छन् - लम्बाइ र चौडाइ मात्र 2D आकार हो। दुई-आयामी आकारहरूको कुनै मोटाई छैन। पक्षहरू सीधा वा घुमाउरो रेखाहरू बनाइएका छन्। तिनीहरूसँग पक्षहरूको कुनै पनि संख्या हुन सक्छ।
दुई आयामको अवधारणालाई समतल सतहको रूपमा सोच्न सकिन्छ जसमा कुनै पनि ठाउँमा सार्न सक्षम हुन्छ। समतल सतहलाई विमान भनिन्छ। 2D आकार भनेको सधैं कागजको पानामा रहेको चीज हो। यसको कुनै उचाइ छैन, र त्यसैले यो कागजको टुक्रा भन्दा माथि पर्दैन। 2D आकारहरू प्लेन आकारहरू वा प्लेन फिगरहरू पनि भनिन्छ।
2D आकारहरूमा क्षेत्र छ तर भोल्युम छैन।
आकृतिहरूको विशेषताहरू रूपरेखा गर्न तीन महत्त्वपूर्ण सर्तहरू छन्:
पक्षहरू - एउटा रेखा खण्ड जसले 2-आयामी चित्रमा आकार बनाउँछ।
ठाडो - एक चित्र को एक कुना।
कोणहरू - ज्यामितिमा, कोणलाई साझा बिन्दुमा दुई रेखाहरू मिलेर बनेको चित्रको रूपमा परिभाषित गर्न सकिन्छ।
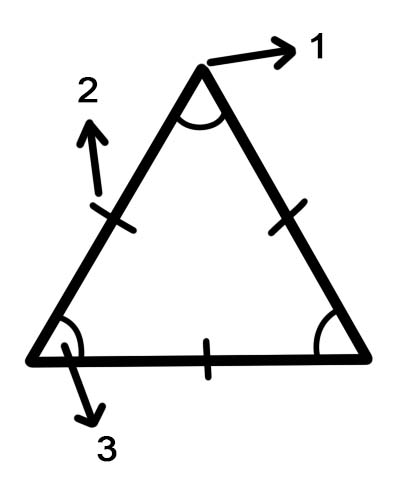
1. vertex
2. पक्षहरू
3. कोण
विभिन्न 2D आकारहरू छलफल गरौं।

वृत्त गोलाकार आकारको आकृति हो जसको कुनै कुना वा किनारा हुँदैन। हामी हाम्रो वरपर कारको टायर, भित्ता घडी र ललीपपमा सर्कलको आकार फेला पार्न सक्छौं। वृत्तको केन्द्र भनेको सर्कलको केन्द्र बिन्दु हो, जहाँबाट सर्कलमा रहेका बिन्दुहरूका सबै दूरीहरू बराबर हुन्छन्। केन्द्रबाट वृत्तको कुनै पनि बिन्दुसम्मको दूरीलाई त्रिज्या भनिन्छ। यदि हामीले सर्कल भरिको दूरीलाई मध्यमा पार गर्दै विचार गर्छौं भने, त्यो व्यास हो। वृत्तको वरिपरिको दूरीलाई वृत्तको परिधि भनिन्छ।
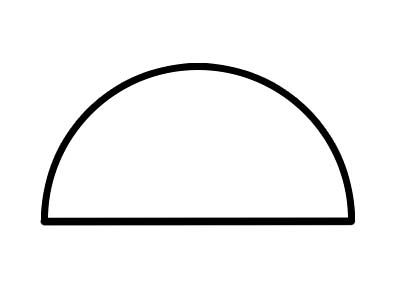
अर्धवृत्त भनेको आधा वृत्त हो, जसलाई माथि देखाइएको व्यास रेखाको साथमा पूरै वृत्त काटेर बनाइन्छ। वृत्तको कुनै पनि व्यासले यसलाई दुई बराबर अर्धवृत्तमा काट्छ। अर्धवृत्तको पूर्ण चाप सधैं 180° मापन गर्दछ। यदि कुकीलाई दुई भागमा काटिएको छ भने, प्रत्येक आधा अर्धवृत्त हुन्छ।

अंडाकारमा अण्डाको रूप, आकार वा रूपरेखा हुन्छ। अंडाकारको कुनै सीधा पक्षहरू र कुनाहरू हुँदैनन्, तर यसको 1 अनुहार हुन्छ, जुन ट्रेस गर्न सकिन्छ वा यसलाई हेर्दा समतल आकारको रूपमा देख्न सकिन्छ।
बहुभुज सीधा रेखाहरू भएको समतल आकार हो। उदाहरणहरूमा त्रिकोणहरू, चतुर्भुजहरू, पेन्टागनहरू, हेक्सागनहरू र यस्तै अन्य समावेश छन्। नियमित बहुभुजमा सबै पक्षहरू बराबर र सबै कोणहरू बराबर हुन्छन्। अन्यथा, यो एक अनियमित बहुभुज हो।
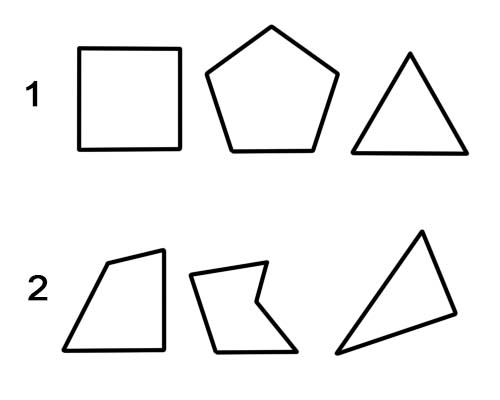
1. नियमित बहुभुज।
2. अनियमित बहुभुज।
वक्रहरू समावेश गर्ने वृत्तहरू र आकारहरू बहुभुज होइनन् - बहुभुज, परिभाषा अनुसार, सीधा रेखाहरू मिलेर बनेको हुन्छ।

ज्यामितिमा, त्रिकोण भनेको बन्द, दुई-आयामी आकार हो जसमा तीनवटा सीधा रेखाहरू हुन्छन्। त्रिभुज पनि बहुभुज हो।
हामी झण्डा, सडकको किनारा साइनबोर्ड र स्यान्डविचमा त्रिकोणको आकार फेला पार्न सक्छौं।
त्रिभुजमा तीनवटा भुजाहरू, तीनवटा ठाडोहरू र तीन कोणहरू हुन्छन्।
त्रिभुजको तीनवटा भित्री कोणहरूको योगफल सधैं 180° हुन्छ। त्रिभुजको दुई पक्षको लम्बाइको योगफल सधैं तेस्रो पक्षको लम्बाइभन्दा ठूलो हुन्छ।
त्रिभुजहरूलाई तिनीहरूको कोण अनुसार वर्गीकरण गर्न, हामी यसको प्रत्येक भित्री कोणहरू मापन गर्छौं। त्रिभुजहरूलाई कोणद्वारा वर्गीकृत गर्न सकिन्छ, यसरी:
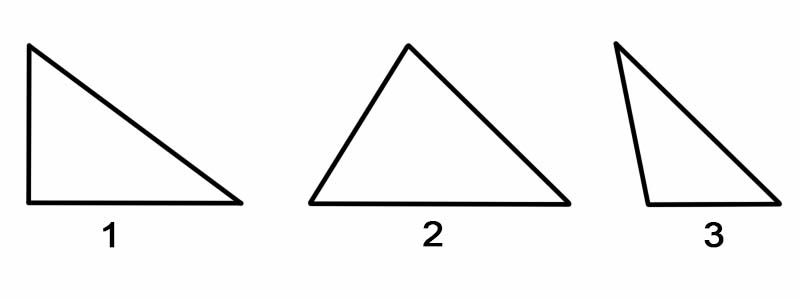
त्रिकोणहरूलाई तिनीहरूको भुजा अनुसार वर्गीकरण गर्न, हामी यसको प्रत्येक पक्षको लम्बाइ नाप्छौं। त्रिभुजहरूलाई तिनीहरूको पक्षद्वारा वर्गीकृत गर्न सकिन्छ, निम्नानुसार:
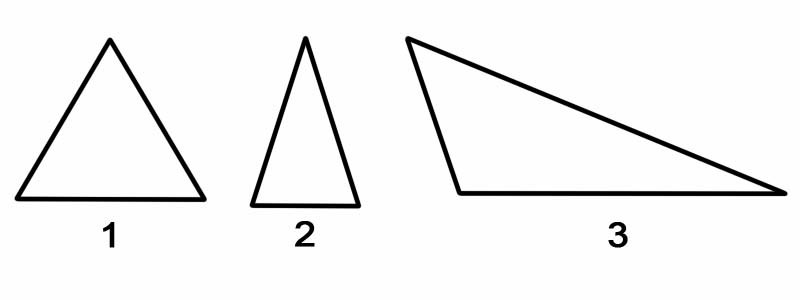
याद गर्नुहोस्: एक त्रिकोण जहिले पनि दुई समकोण त्रिभुजमा विभाजित गर्न सकिन्छ, यसको अभिमुखीकरणको बावजूद।
त्रिभुजहरू कम्तिमा भुजाहरू भएका बहुभुजहरू हुन्।
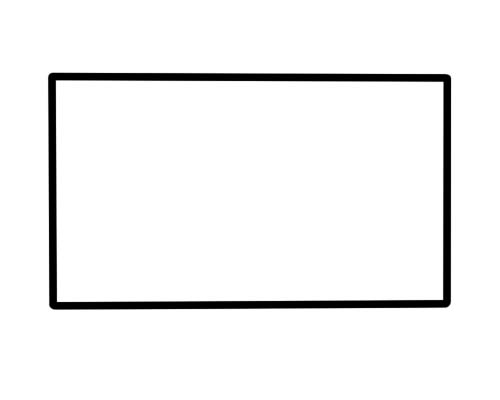
आयत एउटा आकार हो जसमा ४ वटा पक्ष, ४ वटा ठाउ र ४ कोण हुन्छन्। विपरित पक्षहरू समानान्तर र लम्बाइमा बराबर छन्। सबै 4 कोणहरू 90 डिग्री नाप्छन्।
टेबल, बाकस, किताब, ढोका र कागज आयताकार जस्तै देखिन्छ।

रोमबस 4 सीधा रेखाहरु द्वारा बनाईएको आकार हो। यसको 4 पक्षहरू समान लम्बाइ मापन गर्छन् तर, आयतको विपरीत, सबै 4 कोणहरू मध्ये कुनै पनि 90 डिग्री मापन गर्दैन। एक रोमबस हीरा जस्तै देखिन्छ। विपरित पक्षहरू समानान्तर हुन्छन् र विपरीत कोणहरू बराबर हुन्छन्। रोमबसका दुई विकर्णहरू एकअर्कामा लम्ब हुन्छन्।

वर्ग भनेको दुई-आयामी आकृति हो जसको चारै तिरको लम्बाइ बराबर हुन्छ र दुई विपरित भुजाहरू एकअर्कासँग समानान्तर हुन्छन्। यो एक प्रकारको आयत र समभुज (तल छलफल गरिएको) हो। वर्गको 4 भित्री कोणहरू 90º हुन्, वा अर्को शब्दमा, तिनीहरू सही कोण हुन्। जब सबै कोणहरू एकसाथ जोडिन्छन्, तिनीहरूले 360º सम्म जोड्छन्। वर्गको दुई विकर्ण लम्बाइ बराबर हुन्छ र तिनीहरूले पार गरेको बिन्दु वर्गको केन्द्र हो।
याद गर्नुहोस्: वर्ग सधैं एक समभुज हो तर एक समभुज सधैं वर्ग होइन। यदि समभुजको प्रत्येक कोण 90o छ भने मात्र यो वर्ग हुन्छ।
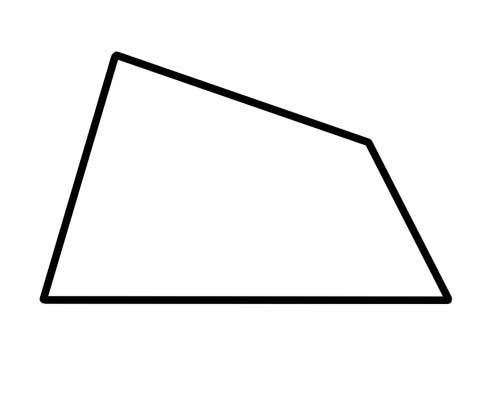
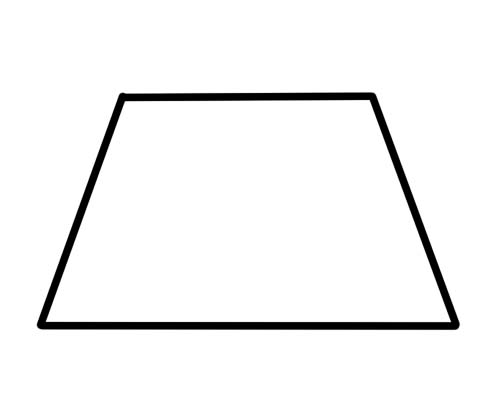
ट्रापेजियम भनेको दुईवटा पार्श्व समानान्तर भएको चतुर्भुज हो।
त्यही भयो। कुनै पनि पक्षहरू समानुपातिक (वा बराबर) हुनु आवश्यक छैन र कुनै कोणहरू समरूप हुनु आवश्यक छैन। कर्णहरूसँग विशेष केही हुँदैन। एक विशेष प्रकारको ट्रापेजियम भनेको 'आइसोसेल्स ट्रापेजियम' हो जसको एउटै लम्बाइका विपरित पक्षहरू र एउटै नापका विपरीत कोणहरू हुन्छन्। विकर्णहरू पनि बराबर लम्बाइका हुन्छन्।
समद्विभुज त्रिकोणमा, छेउछाउका कोणहरू (एक अर्काको छेउमा रहेका कोणहरू) पूरक हुन्छन्। यसको मतलब तिनीहरू 180 डिग्री सम्म जोड्छन्।
ट्रापेजियम एक समानान्तर चतुर्भुज होइन किनभने विपरीत पक्षहरूको मात्र एक जोडी समानान्तर छ।
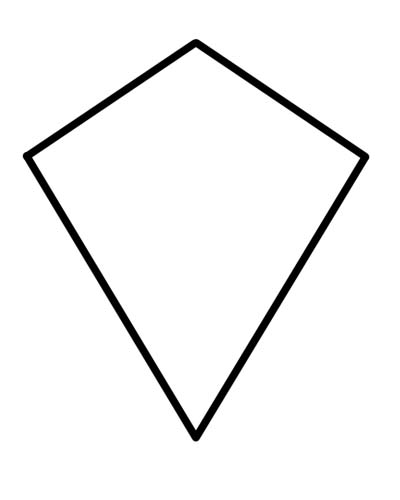
काइट भनेको चतुर्भुज हो जसमा ठ्याक्कै दुई जोडी बराबरको लगातार पक्ष हुन्छ वा जसमा लगातार दुईवटा जोडिने जोडीहरू एकरूप हुन्छन् (विच्छेदन जोडी भनेको दुवै जोडीमा एक पक्ष प्रयोग गर्न सकिँदैन)।
तपाईंले जान्न आवश्यक छ कि प्रत्येक रोमबस एक चंगा हो, किनकि रोम्बसले पतंगका सबै गुणहरूलाई सन्तुष्ट गर्दछ। विपरित पक्षहरू समानान्तर भएको पतंग निश्चित रूपमा समभुज बन्छ। यसरी हरेक रोम्बस काइट हो तर यसको विपरित होइन। पतंग समानान्तर चतुर्भुज होइन किनभने विपरीत पक्षहरू एकअर्कासँग समानान्तर छैनन्।
चतुर्भुज - चार-पक्षीय आकृतिलाई चतुर्भुज भनिन्छ
समानान्तर चतुर्भुज - एक समानान्तर चतुर्भुज एक समतल आकार हो जसको विपरीत पक्षहरू समानान्तर र लम्बाइमा बराबर हुन्छ।
यसरी, आयत, वर्ग, समभुज, ट्रापेजियम र काइट आकारहरू चतुर्भुज हुन् किनभने तिनीहरूका प्रत्येक चारवटा पक्ष हुन्छन्।
यद्यपि, केवल आयत, वर्ग र रम्बस समानान्तर चतुर्भुज हुन्।
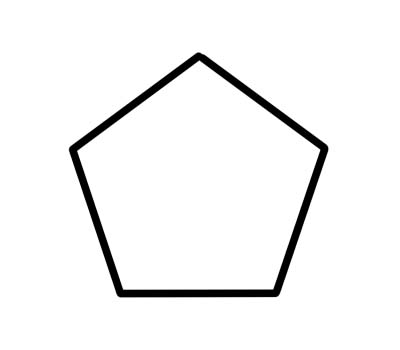
पेन्टागन भनेको ५ वटा भित्री कोण भएको ५ पक्षीय बहुभुज हो जुन ५४० डिग्रीमा जोडिन्छ। नियमित पेन्टागनहरूमा बराबर लम्बाइका पक्षहरू हुन्छन् र प्रत्येक भित्री कोण 108 डिग्रीको हुन्छ।
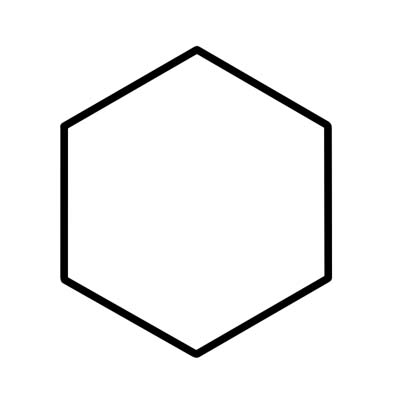
हेक्सागन भनेको ६ वटा भित्री कोण भएको ६-पक्षीय बहुभुज हो जुन ७२० डिग्रीमा जोडिन्छ। अनियमित हेक्सागनको विभिन्न लम्बाइका पक्षहरू हुन्छन्।
एक नियमित षट्भुज बराबर लम्बाइका पक्षहरू हुन्छन् र प्रत्येक भित्री कोण 120 डिग्रीको हुन्छ। एक नियमित षट्भुज छ वटा समभुज त्रिकोणबाट बनेको हुन्छ जसको प्रत्येक केन्द्रीय कोण 60 डिग्री बराबर हुन्छ।
[छवि सम्मिलित गर्नुहोस्: हेक्सागन छ वटा त्रिभुज र ६० डिग्री नाप्ने एउटा केन्द्रीय कोणमा विभाजित छ]
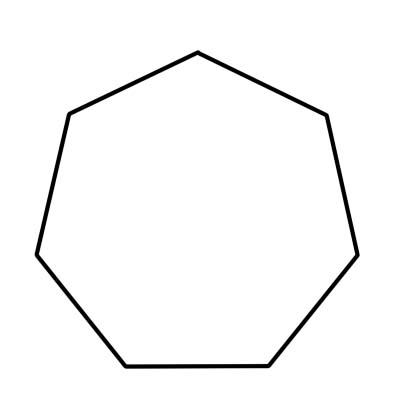
हेप्टागन सात-पक्षीय बहुभुज हो। सात भुजाहरूसँगै, हेप्टागनमा सातवटा ठाडो र कोणहरू हुन्छन्। सबै सात आन्तरिक कोणहरू 900 डिग्रीमा थप्छन्। नियमित हेप्टागनको प्रत्येक भित्री कोणको मापन लगभग 128.57 डिग्री वा लगभग 129 डिग्री हो।
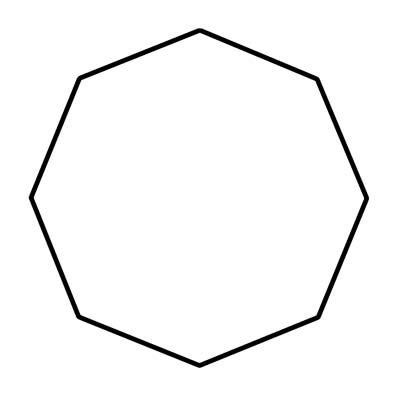
अष्टभुज एक ज्यामितीय आकार हो जसमा आठ पक्ष र आठ कोण हुन्छन्। अष्टागनहरू जोड्ने सीधा पक्षहरू हुनुपर्छ; तिनीहरू वक्र वा विच्छेदन गर्न सकिँदैन। तपाईले प्रायः वास्तविक जीवनमा अष्टभुजहरू स्टप चिन्हको आकारमा देख्नुहुनेछ। नियमित अष्टभुजको प्रत्येक आठ भित्री कोणको नाप लगभग 108 डिग्री हुन्छ। एक उत्तल अष्टभुज भित्र भित्र देखाउने कोण छैन। अझ स्पष्ट रूपमा, कुनै पनि आन्तरिक कोणहरू 180° भन्दा बढी हुन सक्दैन। जब कुनै पनि आन्तरिक कोण 180° भन्दा ठूलो हुन्छ त्यो अवतल हुन्छ
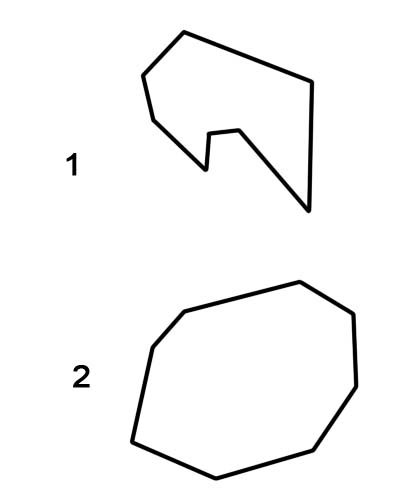
1. अवतल अष्टभुज
2. उत्तल अष्टभुज
यो नोट गर्न महत्त्वपूर्ण छ कि नियमित अष्टभुजहरू सधैं उत्तल अष्टभुजको रूपमा वर्गीकृत गरिन्छ, जबकि अनियमित अष्टभुजहरू अवतल वा उत्तल हुन सक्छन्।
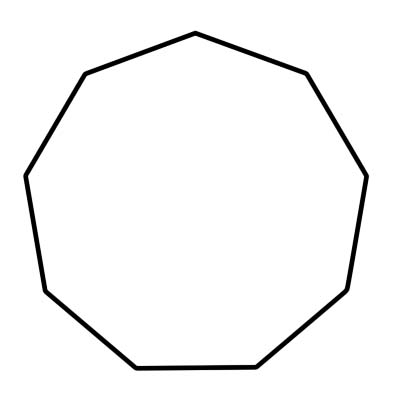
नोनागन भनेको ९ भुजा र ९ भित्री कोण भएको बहुभुज हो जसले १२६० डिग्रीमा जोड्छ। नियमित नोनागनका सबै पक्षहरू समान लम्बाइका हुन्छन् र सबै भित्री कोणहरू समान आकारका हुन्छन्। नियमित नोनागनको कोणको मापन 140 डिग्री हो। एक नोनागन 9 त्रिकोणहरू मिलेर बनेको हुन्छ जसको प्रत्येक केन्द्रीय कोण 40 डिग्री बराबर हुन्छ।
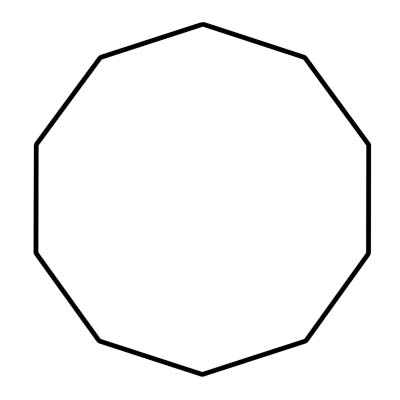
डेकागन १०-पक्षीय बहुभुज हो। यसमा दसवटा ठाडोहरू पनि छन् - जहाँ पक्षहरू मिल्छन् - र कोणहरू। डेकागनको भित्री कोणहरूको योगफल 1440 डिग्री हो। नियमित दशभुजमा समरूप पक्षहरू र कोणहरू हुन्छन्। प्रत्येक कोण 144 डिग्री मापन गर्दछ। एक दशभुज 10 त्रिभुजहरू मिलेर बनेको हुन्छ जसको केन्द्रीय कोण 36 डिग्री बराबर हुन्छ।
तीन दिशामा मापन गर्न सकिने आकारहरूलाई त्रि-आयामिक आकारहरू वा थ्रीडी आकारहरू भनिन्छ। थ्रीडी आकारहरूलाई ठोस आकारहरू पनि भनिन्छ। थ्रीडी आकारका तीन मापनहरू हुन् - लम्बाइ, चौडाइ र उचाइ (वा गहिराइ वा मोटाई)।
3D आकारहरू 2D आकारहरू भन्दा फरक छन् किनभने तिनीहरूको मोटाई छ। हाम्रो दैनिक जीवनबाट थ्रीडी आकारका केही उदाहरणहरू निम्न हुन्:
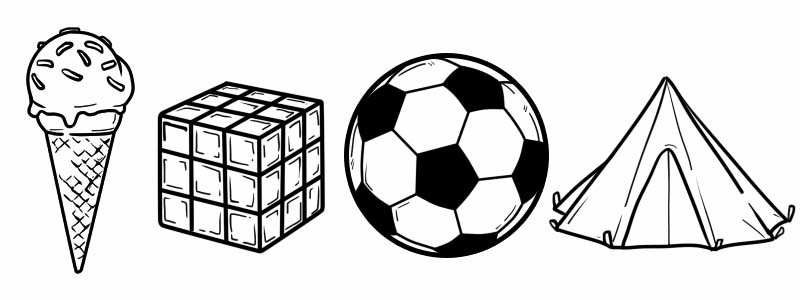
त्रि-आयामी आकारहरूमा ठाडो, अनुहार र किनारहरू छन्।
प्रिज्म एक प्रकारको त्रि-आयामी (3D) आकारको समतल पक्ष हो। यसमा दुईवटा छेउहरू छन् जुन एउटै आकार र आकारका छन् (र 2D आकार जस्तो देखिन्छ)। यसको छेउ देखि अन्त सम्म आकार सहित सबै समान क्रस-सेक्शन छ; यसको मतलब यदि तपाईले यसलाई काट्नु भयो भने तपाईले दुबै छेउमा जस्तै 2D आकार देख्नुहुनेछ।
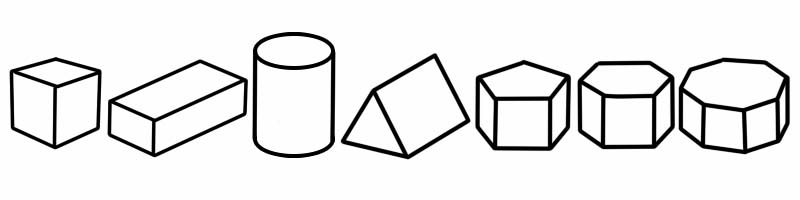
3D आकार | किनाराहरूको संख्या | अनुहारहरूको संख्या | ठाडो संख्या |
घन | १२ | ६ | ८ |
घनाकार | १२ | ६ | ८ |
सिलिन्डर | २ | ३ | ० |
त्रिकोणीय प्रिज्म | ९ | ५ (२ त्रिकोण, ३ आयताकार) | ६ |
पेन्टागोनल प्रिज्म | १५ | ७ | १० |
हेक्सागोनल प्रिज्म | १८ | ८ | १२ |
अष्टभुज प्रिज्म | २४ | १० | १६ |
पिरामिड पनि त्रि-आयामी (3D) आकार हो। यसमा बहुभुज आधार र समतल (त्रिभुज) पक्षहरू छन् जुन एक साझा बिन्दुमा जोडिन्छन् (जसलाई शीर्ष भनिन्छ)। जब 'पिरामिड' शब्दको उल्लेख गरिन्छ, हाम्रो दिमागमा आउने पहिलो कुरा इजिप्टका प्रसिद्ध पिरामिडहरू हुन्। इजिप्शियन पिरामिडहरू वर्ग-आधारित पिरामिडहरू हुन्, तर त्यहाँ धेरै अन्य प्रकारका पिरामिडहरू छन्, प्रत्येकको आधारको रूपमा फरक बहुभुज भएको छ।
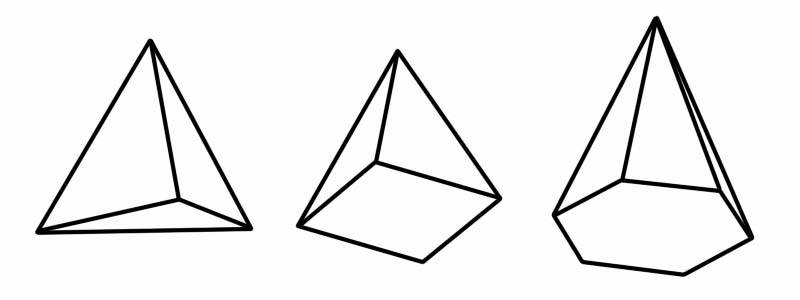
आकार | किनाराहरूको संख्या | अनुहारहरूको संख्या | ठाडो संख्या |
टेट्राहेड्रन | ६ | ४ | ४ |
वर्ग पिरामिड | ८ | ५ | ५ |
हेक्सागोनल पिरामिड | १२ | ७ | ७ |
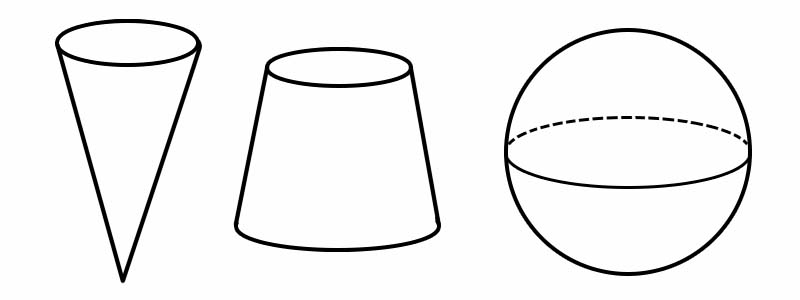
आकार | किनाराहरूको संख्या | अनुहारहरूको संख्या | ठाडो संख्या |
सोली | १ | २ | १ |
फ्रस्टम | २ | ३ | ० |
गोला | ० | १ | ० |