Observeer de verschillende objecten om je heen. Ze zijn er in verschillende soorten en maten. Sommige zijn hetzelfde en sommige zijn anders. Hoewel we de vormen van alle objecten niet precies kunnen noemen, hebben we het in de wiskunde grotendeels over 2D-vormen en 3D-vormen. Laten we meer over hen te weten komen!
Het woord 2D-vorm verwijst naar een "tweedimensionale" vorm. Een geometrische figuur die twee dimensies heeft - alleen lengte en breedte, is een 2D-vorm. De tweedimensionale vormen hebben geen dikte. De zijkanten zijn gemaakt van rechte of gebogen lijnen. Ze kunnen een willekeurig aantal zijden hebben.
Het concept van twee dimensies kan worden gezien als een plat oppervlak waarop men zich overal kan verplaatsen. Het platte oppervlak staat bekend als een vlak. Een 2D-vorm is iets dat altijd op een vel papier ligt. Het heeft geen hoogte en valt daarom niet boven het stuk papier. 2D-vormen worden ook wel vlakke vormen of vlakke figuren genoemd.
2D-vormen hebben een oppervlakte maar geen volume.
Er zijn drie belangrijke termen om de kenmerken van vormen te schetsen:
Zijkanten - Een lijnsegment dat een vorm vormt op een 2-dimensionale figuur.
Vertices - Een hoek van een figuur.
Hoeken - In de geometrie kan een hoek worden gedefinieerd als de figuur gevormd door twee lijnen die elkaar ontmoeten op een gemeenschappelijk eindpunt.
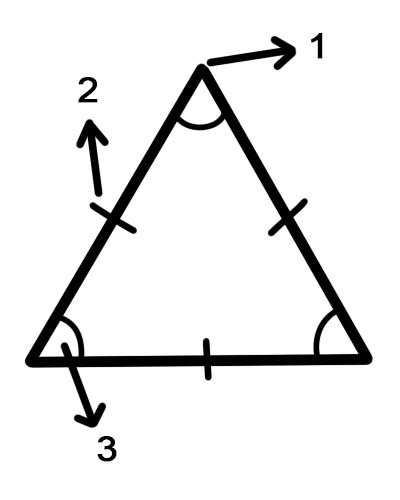
1. hoekpunt
2. kanten
3. hoeken:
Laten we verschillende 2D-vormen bespreken.

Een cirkel is een ronde vorm die geen hoeken of randen heeft. De vorm van een cirkel vinden we om ons heen in een autoband, wandklok en een lolly. Het middelpunt van een cirkel is het middelpunt in een cirkel, van waaruit alle afstanden tot de punten op de cirkel gelijk zijn. De afstand van het middelpunt tot een willekeurig punt op de cirkel wordt de straal genoemd. Als we kijken naar de afstand over de cirkel, door het middelpunt, dan is dat de diameter. De afstand rond een cirkel wordt de omtrek van de cirkel genoemd.
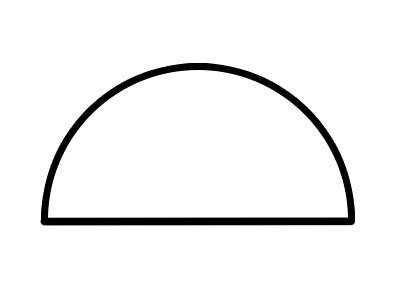
Een halve cirkel is een halve cirkel, gevormd door een hele cirkel langs een diameterlijn te snijden, zoals hierboven weergegeven. Elke diameter van een cirkel snijdt hem in twee gelijke halve cirkels. De volledige boog van een halve cirkel meet altijd 180°. Als een koekje in twee helften wordt gesneden, is elke helft een halve cirkel.

Een ovaal heeft de vorm, vorm of omtrek van een ei. Een ovaal heeft geen rechte zijden en geen hoeken, maar wel 1 gezicht, dat als je ernaar kijkt als een platte vorm te traceren of te zien is.
Een polygoon is een vlakke vorm met rechte lijnen. Voorbeelden zijn driehoeken, vierhoeken, vijfhoeken, zeshoeken enzovoort. Een regelmatige veelhoek heeft alle zijden gelijk en alle hoeken gelijk. Anders is het een onregelmatige veelhoek.
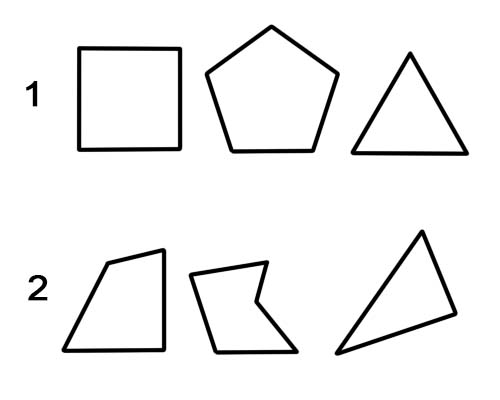
1. Regelmatige veelhoek.
2. Onregelmatige veelhoek.
Cirkels en vormen die krommen bevatten, zijn geen veelhoeken - een veelhoek bestaat per definitie uit rechte lijnen.

In de meetkunde is een driehoek een gesloten, tweedimensionale vorm met drie rechte lijnen. Een driehoek is ook een veelhoek.
De vorm van een driehoek vinden we terug in een vlag, een uithangbord langs de weg en een sandwich.
Een driehoek heeft drie zijden, drie hoekpunten en drie hoeken.
De som van de drie binnenhoeken van een driehoek is altijd 180°. De som van de lengte van twee zijden van een driehoek is altijd groter dan de lengte van de derde zijde.
Om driehoeken te classificeren op basis van hun hoeken, meten we elk van de binnenhoeken. Driehoeken kunnen worden ingedeeld door hoeken, als:
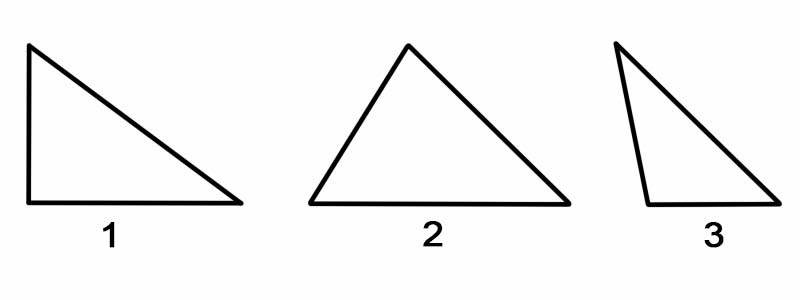
Om de driehoeken volgens hun zijden te classificeren, meten we de lengte van elk van de zijden. Driehoeken kunnen worden ingedeeld naar hun zijden, als:
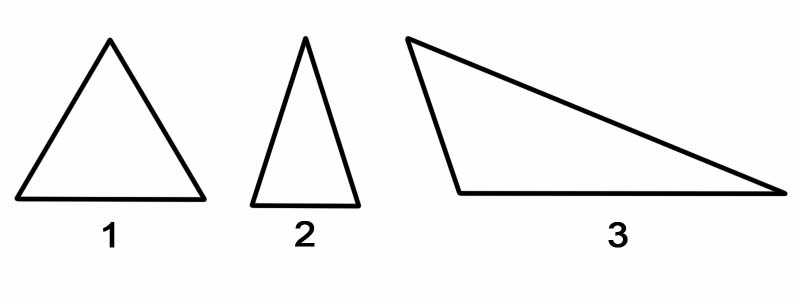
Onthoud: een driehoek kan altijd in twee rechthoekige driehoeken worden gesplitst, ongeacht de oriëntatie.
Driehoeken zijn veelhoeken met het minste aantal zijden.
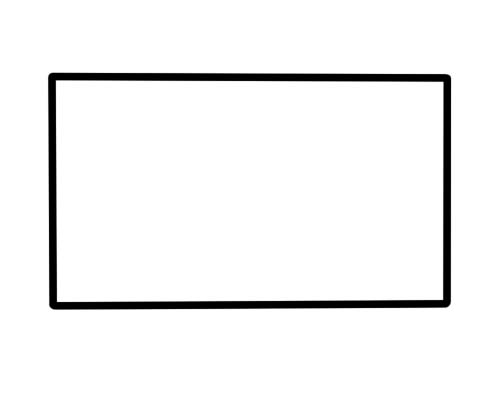
De rechthoek is een vorm met 4 zijden, 4 hoekpunten en 4 hoeken. De tegenoverliggende zijden zijn evenwijdig en even lang. Alle 4 hoeken meten 90 graden.
Tafels, dozen, boeken, deuren en papier zien eruit als rechthoeken.

De ruit is een vorm gevormd door 4 rechte lijnen. De 4 zijden zijn even lang, maar in tegenstelling tot de rechthoek is geen van alle 4 hoeken 90 graden. Een ruit lijkt op een diamant. Overstaande zijden zijn evenwijdig en overstaande hoeken zijn gelijk. De twee diagonalen van een ruit staan loodrecht op elkaar.

Een vierkant is een tweedimensionale figuur waarvan alle vier de zijden even lang zijn en de twee tegenoverliggende zijden evenwijdig aan elkaar. Het is een soort rechthoek en ruit (hieronder besproken). De 4 binnenhoeken van een vierkant zijn 90º, of met andere woorden, het zijn rechte hoeken. Wanneer alle hoeken bij elkaar worden opgeteld, tellen ze op tot 360º. De twee diagonalen die een vierkant heeft, zijn even lang en het punt waar ze elkaar kruisen is het middelpunt van het vierkant.
Onthoud: een vierkant is altijd een ruit, maar een ruit is NIET altijd een vierkant. Als elke hoek van een ruit 90o is, alleen dan is het een vierkant.
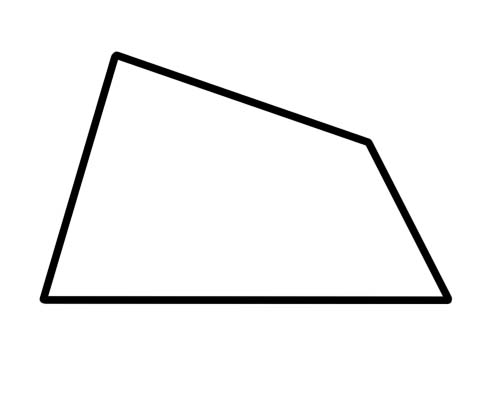
Een trapezium is een vierhoek waarvan slechts twee zijden evenwijdig zijn.
Dat is het. Geen enkele zijde hoeft congruent (of gelijk) te zijn en geen enkele hoek hoeft congruent te zijn. Met de diagonalen gebeurt niets bijzonders. Een speciaal type trapezium is het 'gelijkbenige trapezium' dat overstaande zijden van dezelfde lengte en overstaande hoeken van dezelfde maat heeft. Ook de diagonalen zijn even lang.
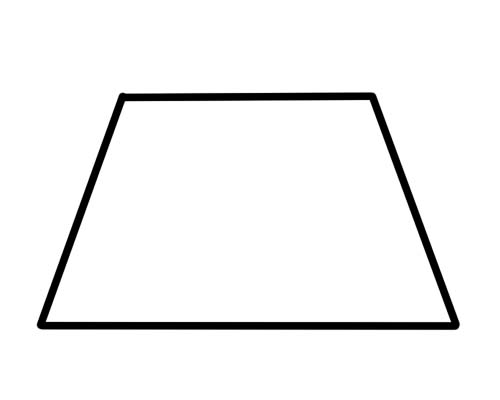
In een gelijkbenige driehoek zijn aangrenzende hoeken langs de zijden (de hoeken naast elkaar) complementair. Dit betekent dat ze optellen tot 180 graden.
Een trapezium is geen parallellogram omdat slechts één paar overstaande zijden evenwijdig is.
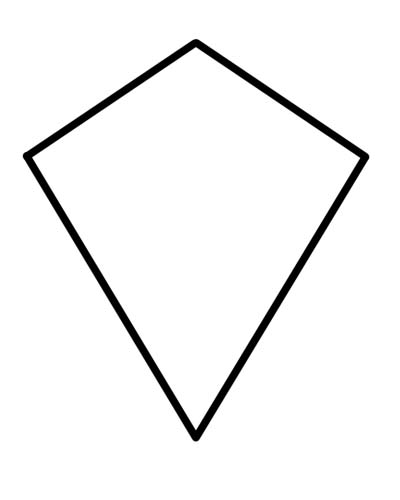
Een vlieger is een vierhoek met precies twee paren van dezelfde opeenvolgende zijde of waarin twee onsamenhangende paren opeenvolgende zijden congruent zijn (disjuncte paren betekent dat één zijde niet in beide paren kan worden gebruikt).
Je moet weten dat elke Rhombus een vlieger is, omdat Rhombus aan alle eigenschappen van een vlieger voldoet. Een vlieger met tegenoverliggende zijden evenwijdig wordt zeker een ruit. Dus elke ruit is een vlieger, maar niet andersom. Een vlieger is geen parallellogram omdat tegenoverliggende zijden niet evenwijdig aan elkaar zijn.
Vierhoeken - Een vierzijdige figuur wordt een vierhoek genoemd
Parallellogram - Een parallellogram is een platte vorm met overstaande zijden evenwijdig en even lang.
Dus rechthoek, vierkant, ruit, trapezium en vlieger vormen zijn vierhoeken omdat ze elk vier zijden hebben.
Alleen rechthoek, vierkant en ruit zijn echter parallellogrammen.
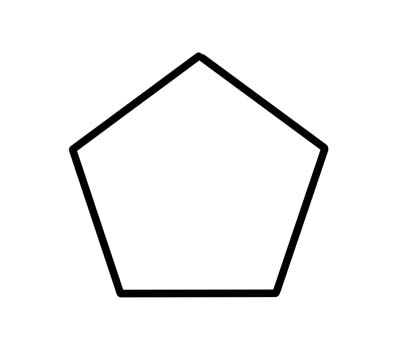
Een Pentagon is een 5-zijdige veelhoek met vijf binnenhoeken die samen 540 graden vormen. Regelmatige vijfhoeken hebben zijden van gelijke lengte en elke binnenhoek is 108 graden.
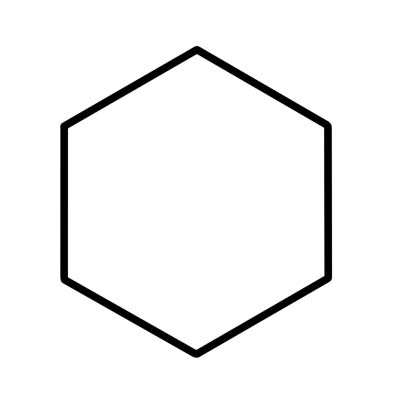
Een zeshoek is een 6-zijdige veelhoek met zes binnenhoeken die samen 720 graden vormen. Onregelmatige zeshoek heeft zijden van verschillende lengte.
Een regelmatige zeshoek heeft zijden van gelijke lengte en elke binnenhoek is 120 graden. Een regelmatige zeshoek bestaat uit zes gelijkzijdige driehoeken met elke centrale hoek gelijk aan 60 graden.
[afbeelding invoegen: zeshoek verdeeld in zes driehoeken en één centrale hoek van 60 graden]
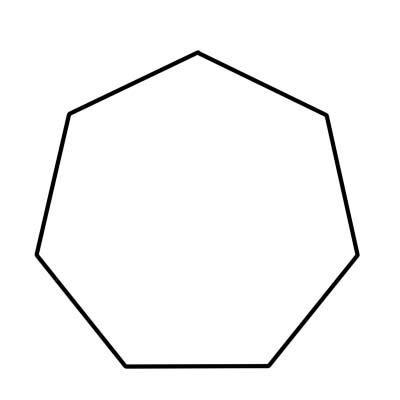
Een zevenhoek is een zevenhoekige veelhoek. Samen met zeven zijden heeft een zevenhoek zeven hoekpunten en hoeken. Alle zeven binnenhoeken vormen samen 900 graden. De maat van elke binnenhoek van een regelmatige zevenhoek is ongeveer 128,57 graden of ongeveer 129 graden.
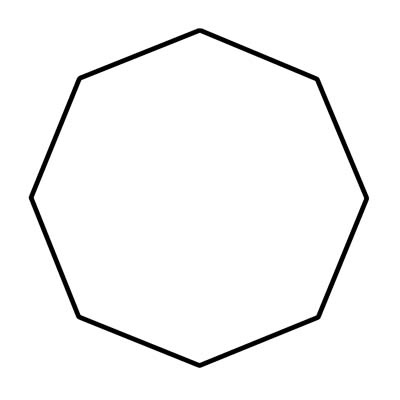
Een achthoek is een geometrische vorm die acht zijden en acht hoeken bevat. Achthoeken moeten rechte zijden hebben die aansluiten; ze kunnen niet worden gebogen of losgekoppeld. In het echt zie je vaak achthoeken in de vorm van een stopbord. De maat van elk van de acht binnenhoeken van een regelmatige achthoek is ongeveer 108 graden. Een convexe achthoek heeft geen naar binnen wijzende hoeken. Om precies te zijn, geen enkele interne hoek kan groter zijn dan 180°. Wanneer een interne hoek groter is dan 180° is deze concaaf
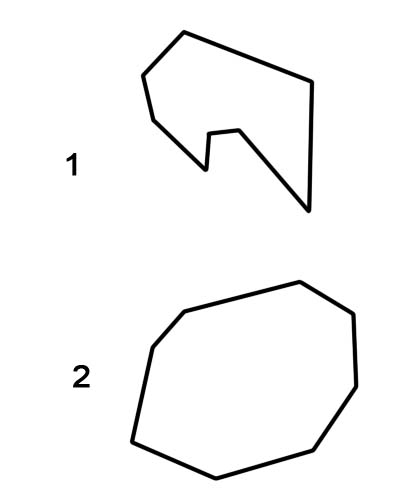
1. Concave achthoek
2. Convexe achthoek
Het is belangrijk op te merken dat regelmatige achthoeken altijd worden geclassificeerd als convexe achthoeken, terwijl onregelmatige achthoeken concaaf of convex kunnen zijn.
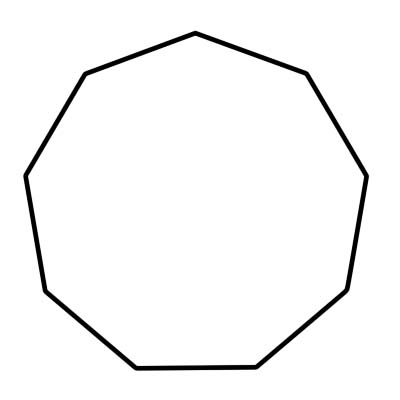
Een nonagon is een veelhoek met 9 zijden en 9 binnenhoeken die samen 1260 graden vormen. Een regelmatige nonagon heeft alle zijden van dezelfde lengte en alle binnenhoeken zijn even groot. De maat van de hoek van een regelmatige nonagon is 140 graden. Een nonagon bestaat uit 9 driehoeken met de maat van elke centrale hoek gelijk aan 40 graden.
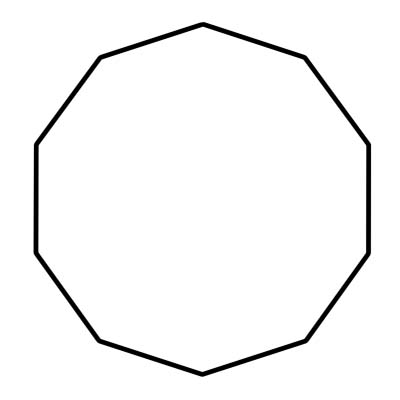
Een tienhoek is een 10-zijdige veelhoek. Het heeft ook tien hoekpunten - waar de zijkanten elkaar ontmoeten - en hoeken. De som van de binnenhoeken van een tienhoek is 1440 graden. Een regelmatige tienhoek heeft congruente zijden en hoeken. Elke hoek meet 144 graden. Een tienhoek bestaat uit 10 driehoeken met een centrale hoek gelijk aan 36 graden.
De vormen die in drie richtingen kunnen worden gemeten, worden driedimensionale vormen of 3D-vormen genoemd. 3D-vormen worden ook wel vaste vormen genoemd. De drie afmetingen van 3D-vormen zijn - Lengte, breedte en hoogte (of diepte of dikte).
3D-vormen verschillen van 2D-vormen omdat ze dik zijn. Enkele voorbeelden van 3D-vormen uit ons dagelijks leven zijn:
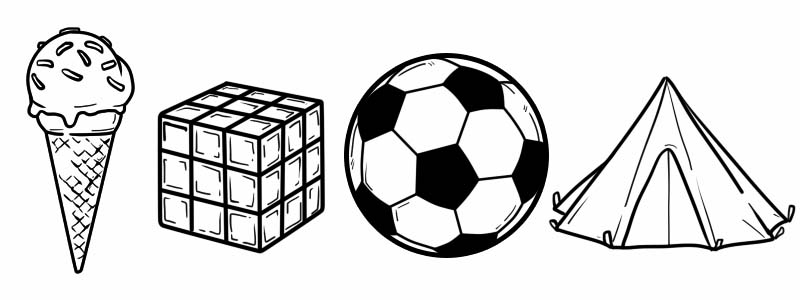
Driedimensionale vormen hebben hoekpunten, vlakken en randen.
Een prisma is een soort driedimensionale (3D) vorm met platte zijden. Het heeft twee uiteinden die dezelfde vorm en grootte hebben (en eruitzien als een 2D-vorm). Het heeft dezelfde dwarsdoorsnede en de vorm van begin tot eind; dat betekent dat als je er doorheen snijdt, je dezelfde 2D-vorm zou zien als aan beide kanten.
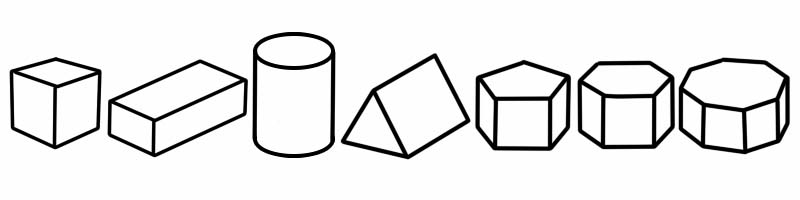
3D-vorm | Aantal randen | Aantal gezichten | Aantal hoekpunten |
Kubus | 12 | 6 | 8 |
kubusvormig | 12 | 6 | 8 |
Cilinder | 2 | 3 | 0 |
Driehoekig Prisma | 9 | 5 (2 driehoeken, 3 rechthoeken) | 6 |
Vijfhoekig prisma | 15 | 7 | 10 |
Zeshoekige Prisma | 18 | 8 | 12 |
achthoekig prisma | 24 | 10 | 16 |
Een piramide is ook een driedimensionale (3D) vorm. Het heeft een veelhoekige basis en platte (driehoekige) zijden die samenkomen op een gemeenschappelijk punt (de apex genoemd). Wanneer het woord 'piramide' wordt genoemd, is het eerste dat in ons opkomt de beroemde piramides van Egypte. De Egyptische piramiden zijn piramides met vierkante basis, maar er zijn verschillende andere soorten piramides, elk met een andere veelhoek als basis.
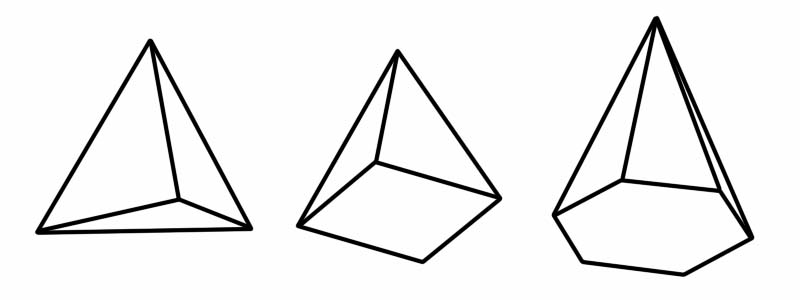
Vorm | Aantal randen | Aantal gezichten | Aantal hoekpunten |
tetraëder | 6 | 4 | 4 |
vierkante piramide | 8 | 5 | 5 |
Zeshoekige piramide | 12 | 7 | 7 |
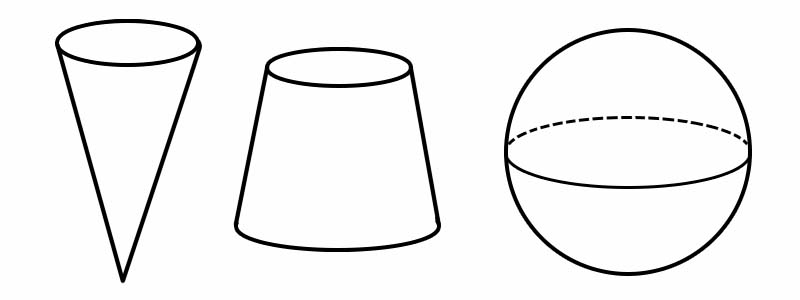
Vorm | Aantal randen | Aantal gezichten | Aantal hoekpunten |
Ijshoorntje | 1 | 2 | 1 |
afgeknot | 2 | 3 | 0 |
Gebied | 0 | 1 | 0 |