Obserwuj różne przedmioty wokół siebie. Występują w różnych kształtach i rozmiarach. Niektóre są takie same, a niektóre inne. Chociaż nie możemy dokładnie nazwać kształtów wszystkich obiektów, w matematyce mówimy głównie o kształtach 2D i kształtach 3D. Dowiedzmy się o nich więcej!
Słowo kształt 2D odnosi się do kształtu „dwuwymiarowego”. Figura geometryczna, która ma tylko dwa wymiary – tylko długość i szerokość, jest kształtem 2D. Dwuwymiarowe kształty nie mają grubości. Boki wykonane są z prostych lub zakrzywionych linii. Mogą mieć dowolną liczbę boków.
Koncepcja dwóch wymiarów może być traktowana jako płaska powierzchnia, po której można się poruszać w dowolnym miejscu. Płaska powierzchnia jest znana jako płaszczyzna. Kształt 2D to coś, co zawsze leży na kartce papieru. Nie ma wysokości, dzięki czemu nie spada ponad kartkę papieru. Kształty 2D są również znane jako kształty płaskie lub figury płaskie.
Kształty 2D mają powierzchnię, ale nie mają objętości.
Istnieją trzy ważne terminy opisujące cechy kształtów:
Boki — odcinek linii, który tworzy kształt na dwuwymiarowej figurze.
Wierzchołki — narożnik figury.
Kąty — w geometrii kąt można zdefiniować jako figurę utworzoną przez dwie proste spotykające się we wspólnym punkcie końcowym.
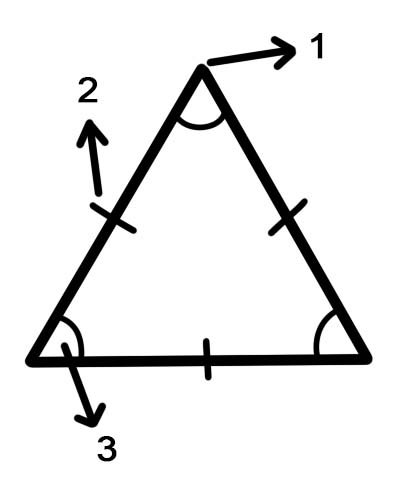
1. wierzchołek
2. strony
3. kąty
Omówmy różne kształty 2D.

Koło to okrągła figura, która nie ma rogów ani krawędzi. Kształt koła możemy znaleźć w oponie samochodowej, zegarze ściennym i lizaku wokół nas. Środek okręgu to punkt środkowy okręgu, od którego wszystkie odległości do punktów na okręgu są sobie równe. Odległość od środka do dowolnego punktu na okręgu nazywana jest promieniem. Jeśli weźmiemy pod uwagę odległość w poprzek koła przechodzącą przez środek, to będzie to średnica. Odległość wokół koła nazywana jest obwodem koła.
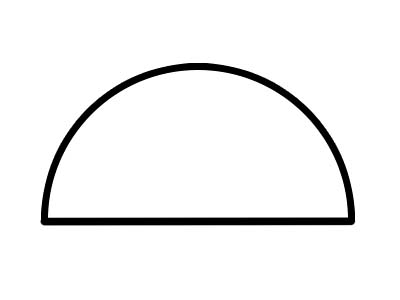
Półkole to półkole utworzone przez wycięcie całego koła wzdłuż linii średnicy, jak pokazano powyżej. Dowolna średnica koła przecina je na dwa równe półkola. Pełny łuk półkola ma zawsze 180°. Jeśli ciastko zostanie przecięte na dwie połówki, to każda połowa będzie półkolem.

Owal ma kształt, kształt lub zarys jajka. Owal nie ma prostych boków ani rogów, ale ma 1 ścianę, którą można prześledzić lub zobaczyć jako płaski kształt, patrząc na nią.
Wielokąt to płaski kształt z liniami prostymi. Przykłady obejmują trójkąty, czworoboki, pięciokąty, sześciokąty i tak dalej. Regularny wielokąt ma wszystkie boki równe i wszystkie kąty równe. W przeciwnym razie jest to nieregularny wielokąt.
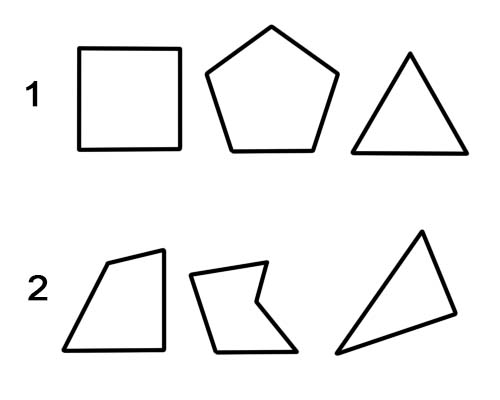
1. Regularny wielokąt.
2. Nieregularny wielokąt.
Okręgi i kształty zawierające krzywe nie są wielokątami — wielokąt z definicji składa się z linii prostych.

W geometrii trójkąt to zamknięty, dwuwymiarowy kształt z trzema liniami prostymi. Trójkąt to też wielokąt.
Kształt trójkąta odnajdziemy we fladze, szyldie przydrożnym i kanapce.
Trójkąt ma trzy boki, trzy wierzchołki i trzy kąty.
Suma trzech kątów wewnętrznych trójkąta wynosi zawsze 180°. Suma długości dwóch boków trójkąta jest zawsze większa niż długość trzeciego boku.
Aby sklasyfikować trójkąty według ich kątów, mierzymy każdy z jego kątów wewnętrznych. Trójkąty można klasyfikować według kątów, jak:
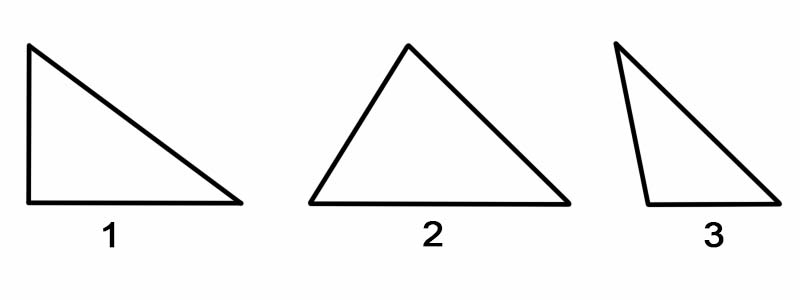
Aby sklasyfikować trójkąty według ich boków, mierzymy długość każdego z jego boków. Trójkąty można klasyfikować ze względu na ich boki jako:
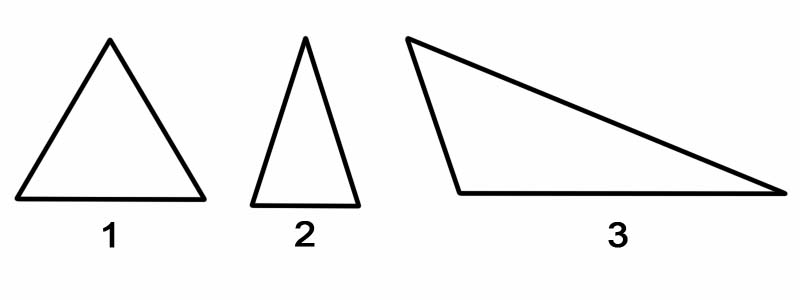
Pamiętaj: trójkąt zawsze można podzielić na dwa trójkąty prostokątne, niezależnie od jego orientacji.
Trójkąty to wielokąty o najmniejszej liczbie boków.
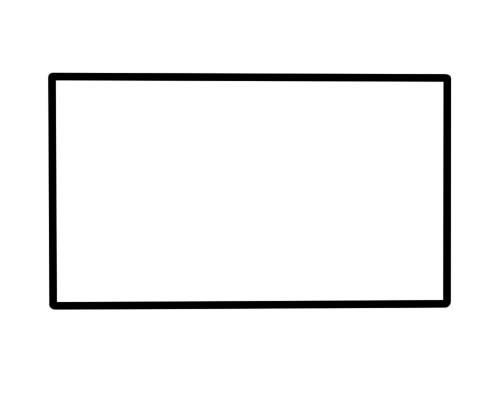
Prostokąt to figura, która ma 4 boki, 4 wierzchołki i 4 kąty. Przeciwległe boki są równoległe i równej długości. Wszystkie 4 kąty mają miarę 90 stopni.
Stoły, pudła, książki, drzwi i papier wyglądają jak prostokąty.

Romb to figura utworzona z 4 prostych. Jego 4 boki mają taką samą długość, ale w przeciwieństwie do prostokąta żaden ze wszystkich 4 kątów nie ma 90 stopni. Romb wygląda jak diament. Przeciwległe boki są równoległe, a przeciwległe kąty są równe. Dwie przekątne rombu są do siebie prostopadłe.

Kwadrat to dwuwymiarowa figura, której wszystkie cztery boki są równej długości, a dwa przeciwległe boki są do siebie równoległe. Jest to rodzaj prostokąta i rombu (omówione poniżej). Cztery kąty wewnętrzne kwadratu mają miarę 90º, czyli innymi słowy są to kąty proste. Kiedy wszystkie kąty są dodane do siebie, sumują się do 360º. Dwie przekątne kwadratu są równej długości, a punkt, w którym się przecinają, jest środkiem kwadratu.
Pamiętaj: Kwadrat jest zawsze rombem, ale romb NIE zawsze jest kwadratem. Jeśli każdy kąt rombu wynosi 90o, tylko wtedy jest to kwadrat.
Trapez to czworokąt, w którym tylko dwa boki są równoległe.
Otóż to. Żadne boki nie muszą być przystające (lub równe) i żadne kąty nie muszą być przystające. Nic specjalnego nie dzieje się z przekątnymi. Specjalnym rodzajem trapezu jest „trapez równoramienny”, który ma przeciwległe boki tej samej długości i przeciwne kąty tej samej miary. Przekątne są również równej długości.
W trójkącie równoramiennym sąsiednie kąty wzdłuż boków (kąty obok siebie) są uzupełniające. Oznacza to, że sumują się do 180 stopni.
Trapez nie jest równoległobokiem, ponieważ tylko jedna para przeciwległych boków jest równoległa.
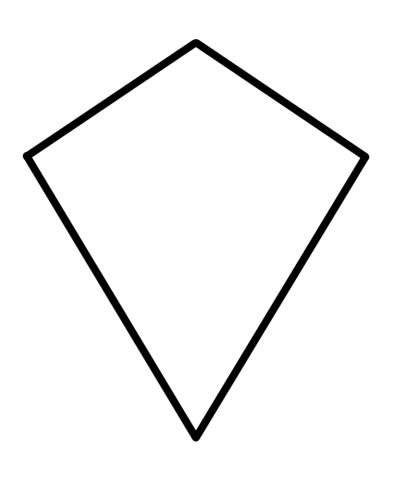
Latawiec to czworokąt, który ma dokładnie dwie pary równych kolejnych boków lub w którym dwie rozłączne pary kolejnych boków są przystające (pary rozłączne oznaczają, że jeden bok nie może być użyty w obu parach).
Musisz wiedzieć, że każdy Rhombus jest latawcem, ponieważ Rhombus spełnia wszystkie właściwości latawca. Latawiec z przeciwległymi bokami równoległymi zdecydowanie staje się rombem. Zatem każdy romb jest latawcem, ale nie odwrotnie. Latawiec nie jest równoległobokiem, ponieważ przeciwległe boki nie są do siebie równoległe.
Czworokąty – czworokątną figurę nazywamy czworobokiem
Równoległobok - Równoległobok to płaski kształt o przeciwległych bokach równoległych i równej długości.
Tak więc kształty prostokąta, kwadratu, rombu, trapezu i latawca są czworobokami, ponieważ każdy z nich ma cztery boki.
Jednak tylko prostokąt, kwadrat i romb są równoległobokami.
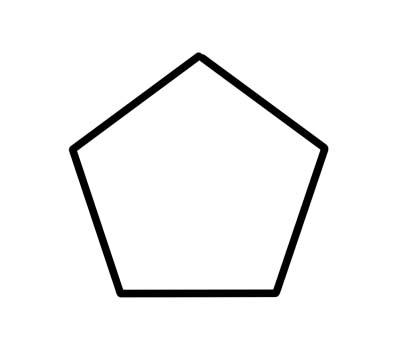
Pentagon to pięcioboczny wielokąt z pięcioma kątami wewnętrznymi, które sumują się do 540 stopni. Regularne pięciokąty mają boki równej długości, a każdy kąt wewnętrzny ma 108 stopni.
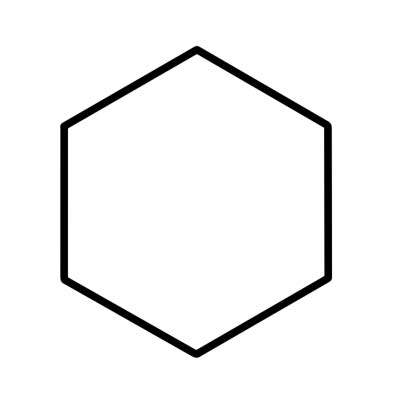
Sześciokąt to sześciokątny wielokąt z sześcioma kątami wewnętrznymi, których suma wynosi 720 stopni. Sześciokąt nieregularny ma boki różnej długości.
Sześciokąt foremny ma boki równej długości, a każdy kąt wewnętrzny ma miarę 120 stopni. Sześciokąt foremny składa się z sześciu trójkątów równobocznych, których każdy kąt środkowy ma miarę 60 stopni.
[wstawić obraz: sześciokąt podzielony na sześć trójkątów i jeden kąt środkowy mierzący 60 stopni]
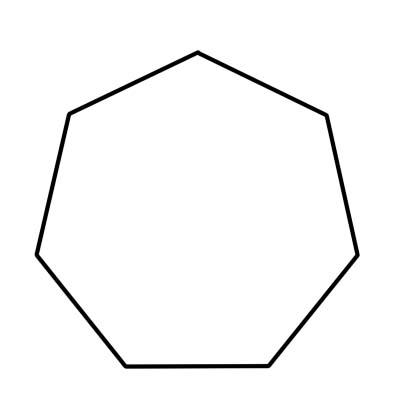
Siedmiokąt to wielokąt o siedmiu bokach. Wraz z siedmioma bokami siedmiokąt ma siedem wierzchołków i kątów. Wszystkie siedem kątów wewnętrznych sumuje się do 900 stopni. Miara każdego kąta wewnętrznego siedmiokąta foremnego wynosi około 128,57 stopnia lub około 129 stopni.
Ośmiokąt to figura geometryczna zawierająca osiem boków i osiem kątów. Ośmiokąty muszą mieć proste boki, które się łączą; nie mogą być zakrzywione ani odłączone. W prawdziwym życiu często zobaczysz ośmiokąty w kształcie znaku stop. Miara każdego z ośmiu kątów wewnętrznych ośmiokąta foremnego wynosi około 108 stopni. Wypukły ośmiokąt nie ma kątów skierowanych do wewnątrz. Dokładniej, żaden kąt wewnętrzny nie może być większy niż 180°. Kiedy dowolny kąt wewnętrzny jest większy niż 180°, jest wklęsły
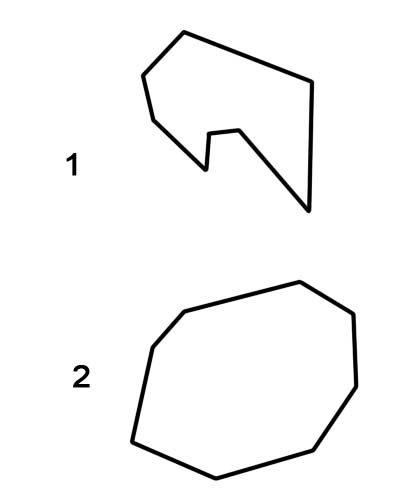
1. Wklęsły ośmiokąt
2. Wypukły ośmiokąt
Należy zauważyć, że ośmiokąty foremne są zawsze klasyfikowane jako ośmiokąty wypukłe, podczas gdy ośmiokąty nieregularne mogą być wklęsłe lub wypukłe.
Dziewięciokąt to wielokąt o 9 bokach i 9 kątach wewnętrznych, których suma wynosi 1260 stopni. Regularny dziewięciokąt ma wszystkie boki tej samej długości i wszystkie kąty wewnętrzne są tego samego rozmiaru. Miara kąta dziewięciokąta foremnego wynosi 140 stopni. Dziewięciokąt składa się z 9 trójkątów o mierze każdego kąta środkowego równej 40 stopni.
Dziesięciokąt to wielokąt o 10 bokach. Ma również dziesięć wierzchołków - czyli miejsca, w którym stykają się boki - i kątów. Suma kątów wewnętrznych dziesięciokąta wynosi 1440 stopni. Regularny dziesięciokąt ma przystające boki i kąty. Każdy kąt ma 144 stopnie. Dziesięciokąt składa się z 10 trójkątów o kącie środkowym równym 36 stopni.
Kształty, które można zmierzyć w trzech kierunkach, nazywane są kształtami trójwymiarowymi lub kształtami 3D. Kształty 3D są również nazywane kształtami bryłowymi. Trzy wymiary kształtów 3D to - Długość, szerokość i wysokość (lub głębokość lub grubość).
Kształty 3D różnią się od kształtów 2D, ponieważ mają grubość. Niektóre przykłady kształtów 3D z naszego codziennego życia to:
Trójwymiarowe kształty mają wierzchołki, ściany i krawędzie.
Pryzmat to rodzaj trójwymiarowego (3D) kształtu o płaskich bokach. Ma dwa końce, które mają ten sam kształt i rozmiar (i wyglądają jak kształt 2D). Ma ten sam przekrój poprzeczny wraz z kształtem od końca do końca; oznacza to, że jeśli go przetniesz, zobaczysz ten sam kształt 2D, co po obu stronach.
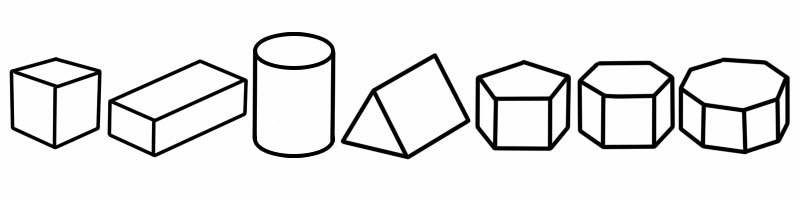
Kształt 3D | Liczba krawędzi | Liczba twarzy | Liczba wierzchołków |
Sześcian | 12 | 6 | 8 |
Prostopadłościan | 12 | 6 | 8 |
Cylinder | 2 | 3 | 0 |
Trójkątny pryzmat | 9 | 5 (2 trójkąty, 3 prostokąty) | 6 |
Pryzmat pięciokątny | 15 | 7 | 10 |
Sześciokątny pryzmat | 18 | 8 | 12 |
Pryzmat ośmiokątny | 24 | 10 | 16 |
Piramida jest również trójwymiarowym (3D) kształtem. Ma wielokątną podstawę i płaskie (trójkątne) boki, które łączą się we wspólnym punkcie (zwanym wierzchołkiem). Kiedy pada słowo „piramida”, pierwszą rzeczą, która przychodzi nam na myśl, są słynne egipskie piramidy. Piramidy egipskie to piramidy oparte na kwadracie, ale istnieje kilka innych typów piramid, z których każda ma inny wielokąt jako podstawę.
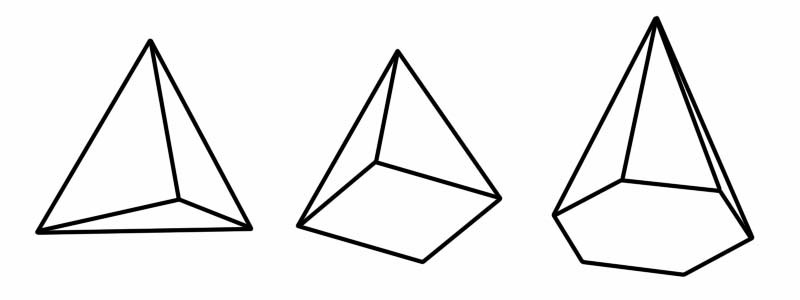
Kształt | Liczba krawędzi | Liczba twarzy | Liczba wierzchołków |
Czworościan | 6 | 4 | 4 |
Kwadratowa Piramida | 8 | 5 | 5 |
Sześciokątna piramida | 12 | 7 | 7 |
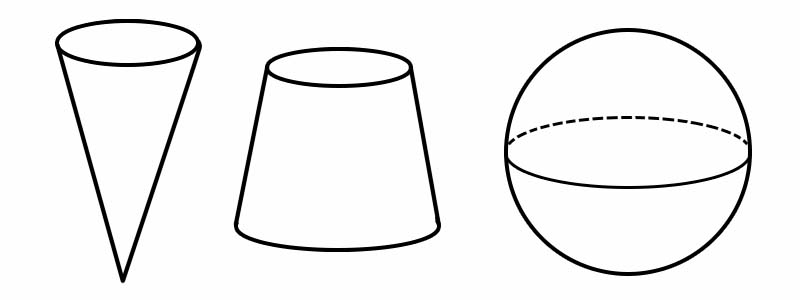
Kształt | Liczba krawędzi | Liczba twarzy | Liczba wierzchołków |
Stożek | 1 | 2 | 1 |
Stożek ścięty | 2 | 3 | 0 |
Kula | 0 | 1 | 0 |