สังเกตสิ่งของต่างๆ รอบตัวคุณ พวกเขามาในรูปทรงและขนาดต่างๆ บางอย่างเหมือนกันและบางอย่างแตกต่างกัน แม้ว่าเราจะไม่สามารถตั้งชื่อรูปร่างของวัตถุทั้งหมดได้อย่างแม่นยำ แต่ในทางคณิตศาสตร์ เรามักจะพูดถึงรูปร่าง 2 มิติและรูปร่าง 3 มิติ มาเรียนรู้เพิ่มเติมเกี่ยวกับพวกเขากันเถอะ!
คำว่ารูปร่าง 2D หมายถึงรูปร่าง "สองมิติ" รูปทรงเรขาคณิตที่มีสองมิติ – ความยาวและความกว้างเท่านั้นที่เป็นรูปร่าง 2 มิติ รูปร่างสองมิติไม่มีความหนา ด้านข้างเป็นเส้นตรงหรือโค้ง พวกมันมีกี่ด้านก็ได้
แนวคิดของสองมิติสามารถคิดได้ว่าเป็นพื้นผิวเรียบซึ่งสามารถเคลื่อนที่ได้ทุกที่ พื้นผิวเรียบเรียกว่าระนาบ รูปร่าง 2 มิติคือสิ่งที่วางอยู่บนกระดาษเสมอ ไม่มีความสูงจึงไม่ตกเหนือแผ่นกระดาษ รูปร่าง 2D เรียกอีกอย่างว่ารูปร่างเครื่องบินหรือตัวเลขเครื่องบิน
รูปร่าง 2D มีพื้นที่แต่ไม่มีปริมาตร
มีคำศัพท์สำคัญสามคำในการร่างลักษณะของรูปร่าง:
ด้านข้าง - ส่วนของเส้นตรงที่สร้างรูปร่างบนร่าง 2 มิติ
จุดยอด - มุมของร่าง
มุม - ในเรขาคณิต มุมสามารถกำหนดเป็นตัวเลขที่เกิดจากเส้นสองเส้นมาบรรจบกันที่จุดสิ้นสุดร่วมกัน
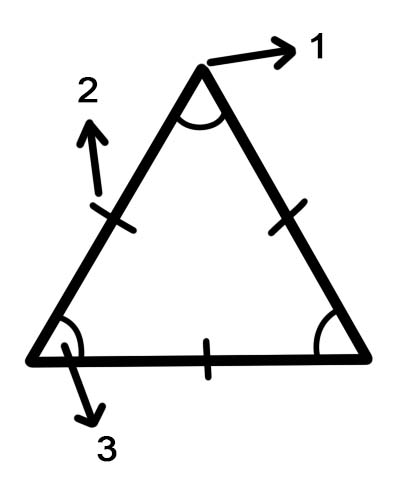
1. จุดยอด
2. ข้าง
3.มุม
มาพูดถึงรูปร่าง 2D ที่แตกต่างกันกัน

วงกลมเป็นรูปทรงกลมที่ไม่มีมุมหรือขอบ เราสามารถหารูปร่างของวงกลมในยางรถยนต์ นาฬิกาแขวน และอมยิ้มได้รอบตัวเรา จุดศูนย์กลางของวงกลมคือจุดศูนย์กลางในวงกลม ซึ่งระยะทั้งหมดถึงจุดบนวงกลมจะเท่ากัน ระยะทางจากจุดศูนย์กลางถึงจุดใดๆ บนวงกลมเรียกว่ารัศมี หากเราพิจารณาระยะทางข้ามวงกลม ผ่านจุดศูนย์กลาง นั่นคือเส้นผ่านศูนย์กลาง ระยะทางรอบวงกลมเรียกว่า เส้นรอบวงของวงกลม
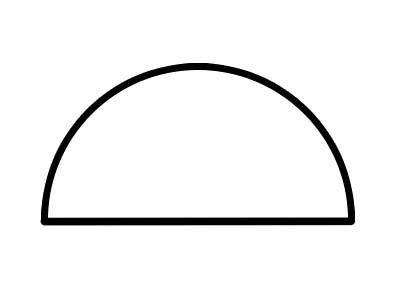
ครึ่งวงกลมเป็นครึ่งวงกลม เกิดขึ้นจากการตัดวงกลมทั้งหมดตามแนวเส้นผ่านศูนย์กลางดังที่แสดงไว้ด้านบน เส้นผ่านศูนย์กลางของวงกลมใดๆ จะตัดเป็นครึ่งวงกลมเท่าๆ กัน ส่วนโค้งเต็มของครึ่งวงกลมวัดได้ 180° เสมอ หากคุกกี้ถูกตัดเป็นสองส่วน แต่ละครึ่งจะเป็นครึ่งวงกลม

วงรีมีรูปร่าง รูปร่าง หรือโครงร่างของไข่ รูปวงรีไม่มีด้านตรงและไม่มีมุม แต่มี 1 หน้า ซึ่งมองดูเป็นรูปวงรีหรือดูแบนๆ ได้
รูปหลายเหลี่ยมเป็นรูประนาบที่มีเส้นตรง ตัวอย่าง ได้แก่ สามเหลี่ยม สี่เหลี่ยม สี่เหลี่ยม ห้าเหลี่ยม หกเหลี่ยม และอื่นๆ รูปหลายเหลี่ยมปกติมีทุกด้านเท่ากันและทุกมุมเท่ากัน มิฉะนั้นจะเป็นรูปหลายเหลี่ยมที่ไม่ปกติ
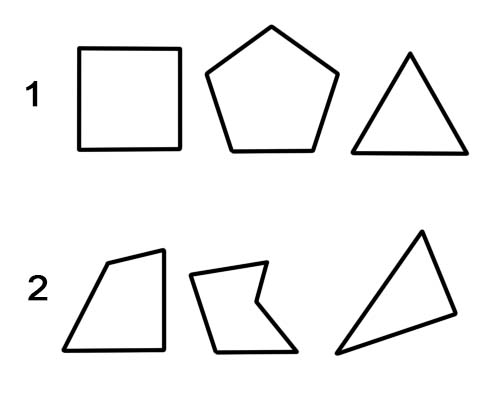
1. รูปหลายเหลี่ยมปกติ
2. รูปหลายเหลี่ยมที่ไม่สม่ำเสมอ
วงกลมและรูปร่างที่มีส่วนโค้งไม่ใช่รูปหลายเหลี่ยม โดยนิยามแล้ว รูปหลายเหลี่ยมประกอบด้วยเส้นตรง

ในเรขาคณิต สามเหลี่ยมเป็นรูปสองมิติปิด มีเส้นตรงสามเส้น สามเหลี่ยมยังเป็นรูปหลายเหลี่ยม
เราสามารถหารูปทรงของสามเหลี่ยมในธง ป้ายข้างถนน และแซนวิช
สามเหลี่ยมมีสามด้าน จุดยอดสามจุด และมุมสามมุม
ผลรวมของมุมภายในทั้งสามของรูปสามเหลี่ยมมีค่าเท่ากับ 180° เสมอ ผลรวมของความยาวของสองด้านของรูปสามเหลี่ยมจะมากกว่าความยาวของด้านที่สามเสมอ
ในการจำแนกสามเหลี่ยมตามมุม เราจะวัดมุมภายในแต่ละมุม สามเหลี่ยมแบ่งตามมุมได้ดังนี้
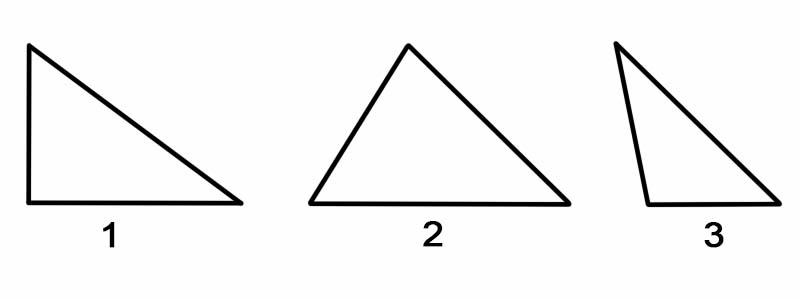
ในการจำแนกสามเหลี่ยมตามด้าน เราวัดความยาวของแต่ละด้าน สามเหลี่ยมแบ่งตามข้างได้ดังนี้
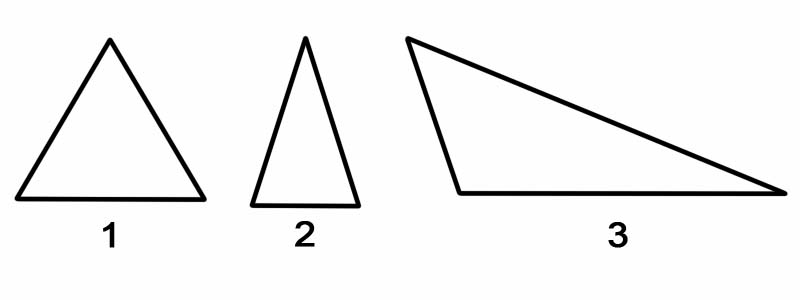
ข้อควรจำ: สามเหลี่ยมสามารถแบ่งออกเป็นสองรูปสามเหลี่ยมมุมฉากได้เสมอ โดยไม่คำนึงถึงทิศทางของมัน
สามเหลี่ยมคือรูปหลายเหลี่ยมที่มีจำนวนด้านน้อยที่สุด
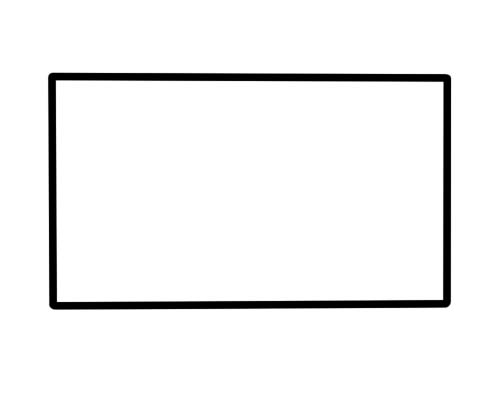
สี่เหลี่ยมผืนผ้า คือ รูปร่างที่มี 4 ด้าน จุดยอด 4 จุด และมุม 4 มุม ด้านตรงข้ามขนานกันและยาวเท่ากัน ทั้ง 4 มุมวัดได้ 90 องศา
โต๊ะ กล่อง หนังสือ ประตู และกระดาษดูเหมือนสี่เหลี่ยม

รูปสี่เหลี่ยมขนมเปียกปูนเป็นรูปทรงที่เกิดจากเส้นตรง 4 เส้น ด้านทั้ง 4 ของมันวัดความยาวเท่ากันแต่ต่างจากสี่เหลี่ยมผืนผ้า ไม่มีมุมทั้ง 4 มุมใดที่วัดได้ 90 องศา รูปสี่เหลี่ยมขนมเปียกปูนดูเหมือนเพชร ด้านตรงข้ามขนานกันและมุมตรงข้ามเท่ากัน เส้นทแยงมุมทั้งสองของรูปสี่เหลี่ยมขนมเปียกปูนตั้งฉากกัน

สี่เหลี่ยมจัตุรัสเป็นรูปสองมิติที่มีด้านทั้งสี่ด้านยาวเท่ากัน และด้านตรงข้ามทั้งสองขนานกัน เป็นรูปสี่เหลี่ยมผืนผ้าและรูปสี่เหลี่ยมขนมเปียกปูน มุมภายใน 4 มุมของสี่เหลี่ยมจัตุรัสคือ 90º หรืออีกนัยหนึ่ง มันคือมุมฉาก เมื่อรวมมุมทั้งหมดเข้าด้วยกัน จะรวมกันได้ 360º เส้นทแยงมุมสองเส้นที่สี่เหลี่ยมจัตุรัสมีความยาวเท่ากัน และจุดที่ข้ามคือจุดศูนย์กลางของสี่เหลี่ยม
ข้อควรจำ: สี่เหลี่ยมจัตุรัสเป็นรูปสี่เหลี่ยมขนมเปียกปูนเสมอ แต่รูปสี่เหลี่ยมขนมเปียกปูนไม่ใช่สี่เหลี่ยมจัตุรัสเสมอไป ถ้าแต่ละมุมของรูปสี่เหลี่ยมขนมเปียกปูนมีค่าเท่ากับ 90o ก็เท่านั้น มันคือสี่เหลี่ยมจัตุรัส
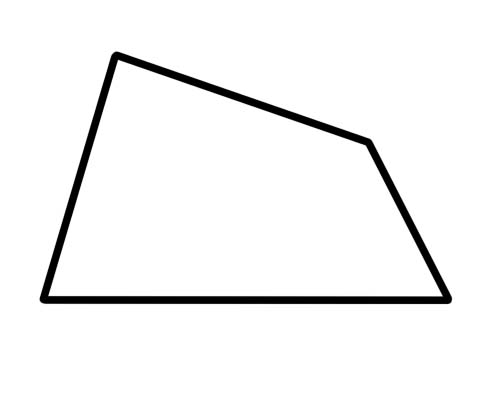
สี่เหลี่ยมคางหมูเป็นรูปสี่เหลี่ยมที่มีสองด้านขนานกันเท่านั้น
แค่นั้นแหละ. ไม่จำเป็นต้องมีด้านเท่ากัน (หรือเท่ากัน) และมุมไม่จำเป็นต้องเท่ากัน ไม่มีอะไรพิเศษเกิดขึ้นกับเส้นทแยงมุม สี่เหลี่ยมคางหมูชนิดพิเศษคือ 'สี่เหลี่ยมคางหมูหน้าจั่ว' ซึ่งมีด้านตรงข้ามกันที่มีความยาวเท่ากันและมีมุมตรงข้ามกันที่มีขนาดเท่ากัน เส้นทแยงมุมก็มีความยาวเท่ากัน
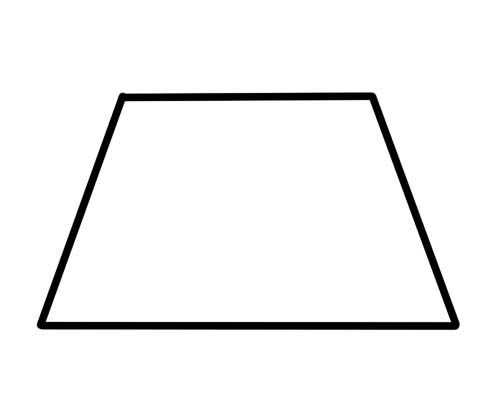
ในรูปสามเหลี่ยมหน้าจั่ว มุมที่อยู่ติดกันด้านข้าง (มุมที่อยู่ติดกัน) เป็นส่วนเสริม ซึ่งหมายความว่ารวมกันได้ 180 องศา
สี่เหลี่ยมคางหมูไม่ใช่สี่เหลี่ยมด้านขนานเพราะมีด้านตรงข้ามขนานกันเพียงคู่เดียว
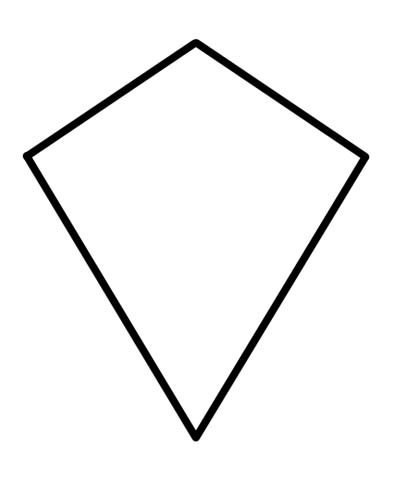
ว่าวเป็นรูปสี่เหลี่ยมที่มีคู่สองคู่ของด้านที่ต่อเนื่องกันเท่ากันหรือสองคู่ที่ไม่ต่อเนื่องกันของด้านที่ต่อเนื่องกันจะเท่ากัน (คู่ที่ไม่ปะติดปะต่อกันหมายความว่าด้านใดด้านหนึ่งไม่สามารถใช้ในทั้งสองคู่ได้)
คุณจำเป็นต้องรู้ว่ารูปสี่เหลี่ยมขนมเปียกปูนทุกตัวเป็นว่าว เนื่องจากรูปสี่เหลี่ยมขนมเปียกปูนมีคุณสมบัติทั้งหมดของว่าว ว่าวที่มีด้านตรงข้ามขนานกันจะกลายเป็นรูปสี่เหลี่ยมขนมเปียกปูนอย่างแน่นอน ดังนั้นรูปสี่เหลี่ยมขนมเปียกปูนทุกตัวจึงเป็นว่าวแต่ไม่ใช่ในทางกลับกัน ว่าวไม่ใช่สี่เหลี่ยมด้านขนานเพราะด้านตรงข้ามไม่ขนานกัน
รูปสี่เหลี่ยม - รูปสี่ด้านเรียกว่ารูปสี่เหลี่ยม
สี่เหลี่ยมด้านขนาน - สี่เหลี่ยมด้านขนานเป็นรูปแบนที่มีด้านตรงข้ามขนานกันและมีความยาวเท่ากัน
ดังนั้น รูปสี่เหลี่ยมผืนผ้า สี่เหลี่ยมจัตุรัส รูปสี่เหลี่ยมขนมเปียกปูน สี่เหลี่ยมคางหมู และรูปว่าว เป็นรูปสี่เหลี่ยมเพราะมันมีสี่ด้านแต่ละด้าน
อย่างไรก็ตาม เฉพาะสี่เหลี่ยม สี่เหลี่ยม และสี่เหลี่ยมขนมเปียกปูนเท่านั้นที่เป็นสี่เหลี่ยมด้านขนาน
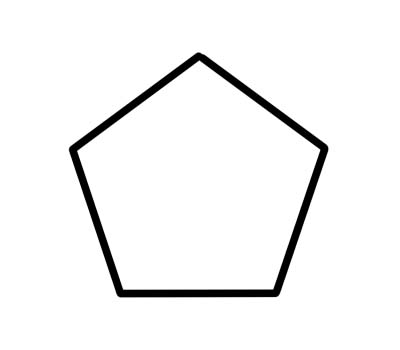
เพนตากอนเป็นรูปหลายเหลี่ยม 5 ด้านที่มีมุมภายในห้ามุมที่รวมกันได้ 540 องศา รูปห้าเหลี่ยมปกติมีด้านยาวเท่ากัน และแต่ละมุมภายในมี 108 องศา
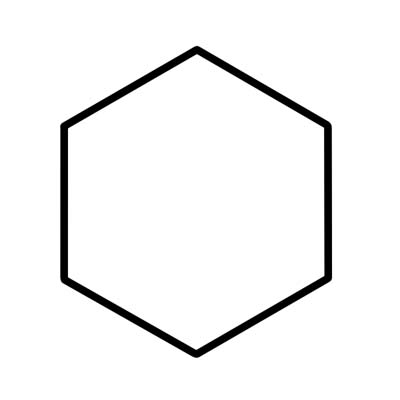
รูปหกเหลี่ยมคือรูปหลายเหลี่ยม 6 ด้านที่มีมุมภายในหกมุมที่รวมกันได้ 720 องศา รูปหกเหลี่ยมไม่ปกติมีด้านที่มีความยาวต่างกัน
รูปหกเหลี่ยมปกติมีด้านยาวเท่ากัน และแต่ละมุมภายในจะเท่ากับ 120 องศา รูปหกเหลี่ยมปกติประกอบด้วยรูปสามเหลี่ยมด้านเท่าหกรูป โดยแต่ละมุมมีมุมศูนย์กลางเท่ากับ 60 องศา
[ภาพแทรก: หกเหลี่ยมแบ่งออกเป็นหกสามเหลี่ยมและหนึ่งมุมตรงกลางวัด 60 องศา]
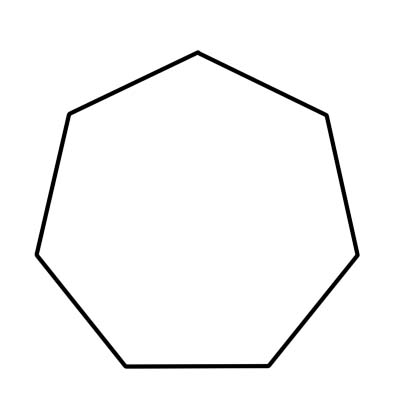
รูปหกเหลี่ยมเป็นรูปหลายเหลี่ยมเจ็ดด้าน นอกจากเจ็ดด้านแล้ว รูปหกเหลี่ยมยังมีจุดยอดและมุมเจ็ดจุด มุมภายในทั้งหมดเจ็ดมุมรวมกันเป็น 900 องศา การวัดมุมภายในแต่ละมุมของรูปหกเหลี่ยมปกติคือประมาณ 128.57 องศาหรือประมาณ 129 องศา
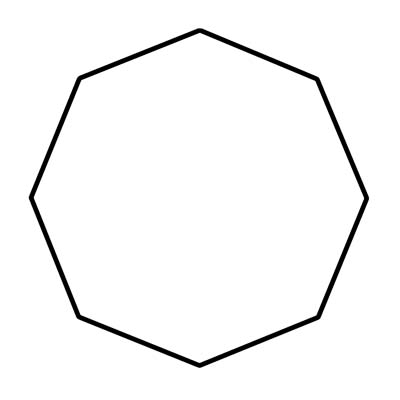
แปดเหลี่ยมเป็นรูปทรงเรขาคณิตที่มีด้านแปดด้านและมุมแปดมุม รูปแปดเหลี่ยมต้องมีด้านตรงที่เชื่อมติดกัน พวกเขาไม่สามารถโค้งหรือตัดการเชื่อมต่อ คุณมักจะเห็นรูปแปดเหลี่ยมในชีวิตจริงในรูปของป้ายหยุด มุมภายในทั้งแปดของรูปแปดเหลี่ยมปกติแต่ละมุมจะวัดได้ประมาณ 108 องศา แปดเหลี่ยมนูนไม่มีมุมชี้เข้าด้านใน แม่นยำยิ่งขึ้น ไม่มีมุมภายในใดเกิน 180° เมื่อมุมภายในใดๆ มากกว่า 180° ก็จะเว้า
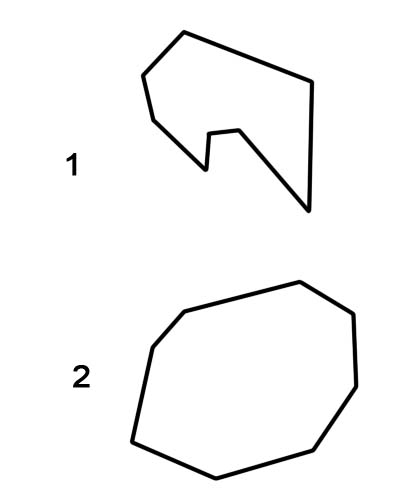
1. เว้าแปดเหลี่ยม
2. แปดเหลี่ยมนูน
สิ่งสำคัญคือต้องสังเกตว่ารูปแปดเหลี่ยมปกติจะจัดเป็นรูปแปดเหลี่ยมนูนเสมอ ในขณะที่รูปแปดเหลี่ยมที่ไม่ปกติสามารถเป็นแบบเว้าหรือนูนก็ได้
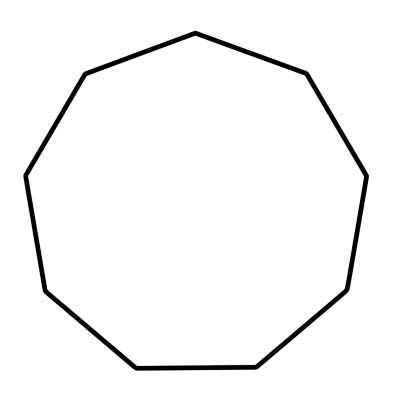
nonagon เป็นรูปหลายเหลี่ยมที่มีด้าน 9 ด้าน และมีมุมภายใน 9 มุม ซึ่งรวมกันได้ 1260 องศา nonagon ปกติมีความยาวเท่ากันทุกด้าน และมุมภายในทั้งหมดมีขนาดเท่ากัน การวัดมุมของ nonagon ปกติคือ 140 องศา nonagon ประกอบขึ้นจากสามเหลี่ยม 9 รูป โดยแต่ละมุมมีมุมศูนย์กลางเท่ากับ 40 องศา
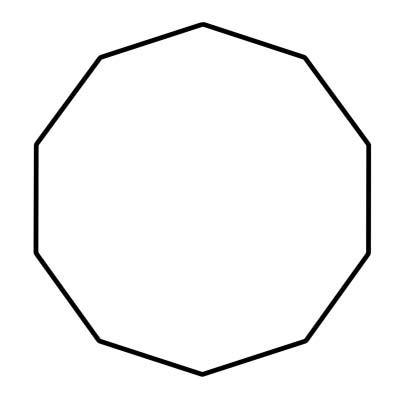
รูปหลายเหลี่ยมเป็นรูปหลายเหลี่ยม 10 ด้าน นอกจากนี้ยังมีจุดยอดสิบจุดซึ่งเป็นจุดที่ด้านบรรจบกันและมีมุม ผลรวมของมุมภายในของหนึ่งรูปห้าเหลี่ยมคือ 1440 องศา รูปหลายเหลี่ยมปกติมีด้านและมุมที่เท่ากัน แต่ละมุมวัดได้ 144 องศา หนึ่งรูปห้าเหลี่ยมประกอบด้วยสามเหลี่ยม 10 รูป โดยมีมุมตรงกลางเท่ากับ 36 องศา
รูปร่างที่สามารถวัดได้ในสามทิศทางเรียกว่ารูปร่างสามมิติหรือรูปร่างสามมิติ รูปร่าง 3 มิติเรียกอีกอย่างว่ารูปร่างทึบ การวัดรูปร่าง 3 มิติทั้งสามแบบคือ - ความยาว ความกว้าง และความสูง (หรือความลึกหรือความหนา)
รูปร่าง 3 มิติแตกต่างจากรูปร่าง 2 มิติเพราะมีความหนา ตัวอย่างรูปร่าง 3 มิติจากชีวิตประจำวันของเรา ได้แก่
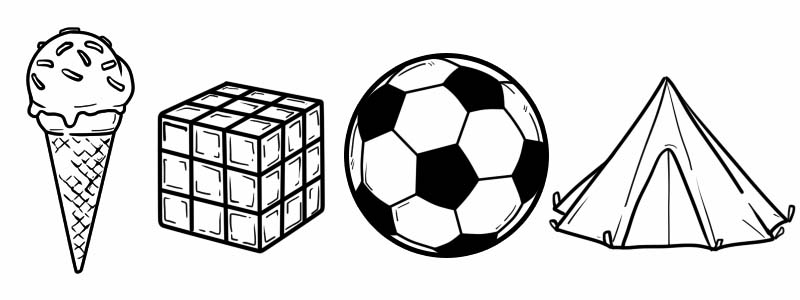
รูปร่างสามมิติมีจุดยอด ใบหน้า และขอบ
ปริซึมเป็นรูปทรงสามมิติ (3D) ที่มีด้านแบน มีปลายทั้งสองด้านที่มีรูปร่างและขนาดเท่ากัน (และดูเหมือนรูปร่าง 2 มิติ) มีหน้าตัดเหมือนกันทุกประการกับรูปร่างตั้งแต่ต้นจนจบ นั่นหมายความว่า ถ้าคุณตัดผ่าน คุณจะเห็นรูปร่าง 2D เหมือนกันที่ด้านใดด้านหนึ่ง
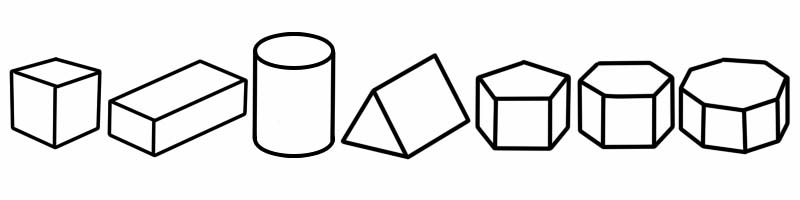
รูปร่าง 3 มิติ | จำนวนขอบ | จำนวนใบหน้า | จำนวนจุดยอด |
คิวบ์ | 12 | 6 | 8 |
ทรงลูกบาศก์ | 12 | 6 | 8 |
กระบอก | 2 | 3 | 0 |
ปริซึมสามเหลี่ยม | 9 | 5 (2 สามเหลี่ยม 3 สี่เหลี่ยม) | 6 |
ปริซึมห้าเหลี่ยม | 15 | 7 | 10 |
ปริซึมหกเหลี่ยม | 18 | 8 | 12 |
ปริซึมแปดเหลี่ยม | 24 | 10 | 16 |
พีระมิดยังเป็นรูปทรงสามมิติ (3D) มีฐานรูปหลายเหลี่ยมและด้านแบน (สามเหลี่ยม) ที่เชื่อมกันที่จุดร่วม (เรียกว่ายอด) เมื่อพูดถึงคำว่า 'ปิรามิด' สิ่งแรกที่เข้ามาในความคิดของเราคือปิรามิดที่มีชื่อเสียงของอียิปต์ ปิรามิดอียิปต์เป็นปิรามิดที่มีฐานเป็นสี่เหลี่ยม แต่มีปิรามิดประเภทอื่นๆ อีกหลายประเภท แต่ละปิรามิดมีฐานต่างกัน
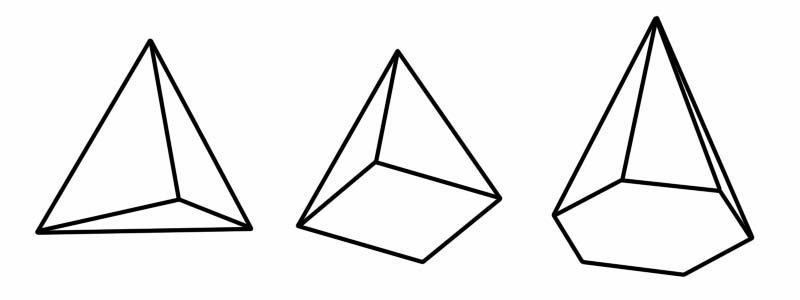
รูปร่าง | จำนวนขอบ | จำนวนใบหน้า | จำนวนจุดยอด |
จัตุรมุข | 6 | 4 | 4 |
พีระมิดสี่เหลี่ยม | 8 | 5 | 5 |
พีระมิดหกเหลี่ยม | 12 | 7 | 7 |
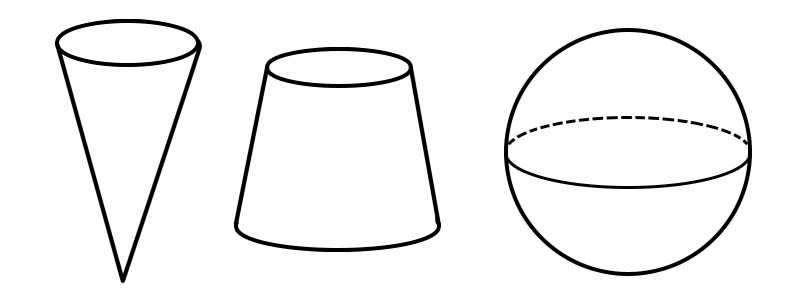
รูปร่าง | จำนวนขอบ | จำนวนใบหน้า | จำนวนจุดยอด |
กรวย | 1 | 2 | 1 |
Frustum | 2 | 3 | 0 |
ทรงกลม | 0 | 1 | 0 |