Pagmasdan ang iba't ibang bagay sa paligid mo. Dumating sila sa iba't ibang hugis at sukat. Ang iba ay pareho at ang iba ay iba. Bagama't hindi namin tiyak na pangalanan ang mga hugis ng lahat ng mga bagay, sa matematika ay higit na pinag-uusapan natin ang tungkol sa mga 2D na hugis at 3D na mga hugis. Matuto pa tayo tungkol sa kanila!
Ang salitang 2D na hugis ay tumutukoy sa isang "two-dimensional" na hugis. Ang isang geometrical na figure na may dalawang dimensyon - haba at lapad lamang ay isang 2D na hugis. Ang dalawang-dimensional na mga hugis ay walang kapal. Ang mga gilid ay gawa sa tuwid o hubog na mga linya. Maaari silang magkaroon ng anumang bilang ng mga panig.
Ang konsepto ng dalawang dimensyon ay maaaring isipin bilang isang patag na ibabaw kung saan ang isa ay nakakagalaw kahit saan. Ang patag na ibabaw ay kilala bilang isang eroplano. Ang 2D na hugis ay isang bagay na laging nakalagay sa isang sheet ng papel. Wala itong taas, at samakatuwid ay hindi ito nahuhulog sa itaas ng piraso ng papel. Ang mga 2D na hugis ay kilala rin bilang mga hugis ng eroplano o mga figure ng eroplano.
Ang mga 2D na hugis ay may lawak ngunit walang volume.
Mayroong tatlong mahahalagang termino upang ibalangkas ang mga katangian ng mga hugis:
Mga Gilid - Isang segment ng linya na bumubuo ng hugis sa isang 2-dimensional na pigura.
Vertices - Isang sulok ng figure.
Mga Anggulo - Sa geometry, ang isang anggulo ay maaaring tukuyin bilang ang figure na nabuo sa pamamagitan ng dalawang linya na nagtatagpo sa isang karaniwang endpoint.
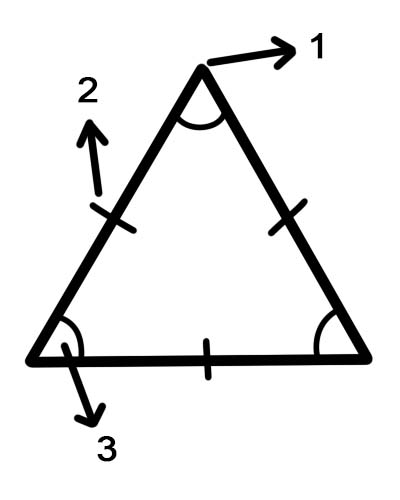
1. vertex
2. panig
3.anggulo
Talakayin natin ang iba't ibang 2D na hugis.

Ang bilog ay isang bilog na hugis na pigura na walang sulok o gilid. Makikita natin ang hugis ng bilog sa gulong ng kotse, wall clock at lollipop, sa paligid natin. Ang gitna ng isang bilog ay ang sentrong punto sa isang bilog, kung saan ang lahat ng mga distansya sa mga punto sa bilog ay pantay. Ang distansya mula sa gitna hanggang sa anumang punto sa bilog ay tinatawag na radius. Kung isasaalang-alang natin ang distansya sa kabuuan ng bilog, na dumadaan sa gitna, iyon ang diameter. Ang distansya sa paligid ng isang bilog ay tinatawag na circumference ng bilog.
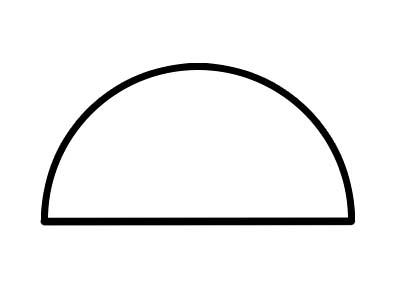
Ang kalahating bilog ay isang kalahating bilog, na nabuo sa pamamagitan ng pagputol ng isang buong bilog sa isang linya ng diameter, tulad ng ipinapakita sa itaas. Anumang diameter ng isang bilog ay pinuputol ito sa dalawang pantay na kalahating bilog. Ang buong arko ng kalahating bilog ay laging may sukat na 180°. Kung ang isang cookie ay pinutol sa dalawang halves, ang bawat kalahati ay kalahating bilog.

Ang isang hugis-itlog ay may anyo, hugis, o balangkas ng isang itlog. Ang isang oval ay walang mga tuwid na gilid at walang sulok, ngunit mayroon itong 1 mukha, na maaaring masubaybayan o makikita bilang isang patag na hugis kapag tinitingnan ito.
Ang polygon ay isang hugis ng eroplano na may mga tuwid na linya. Kasama sa mga halimbawa ang mga triangles, quadrilaterals, pentagons, hexagons at iba pa. Ang isang regular na polygon ay may pantay na panig at lahat ng mga anggulo ay pantay. Kung hindi, ito ay isang hindi regular na polygon.
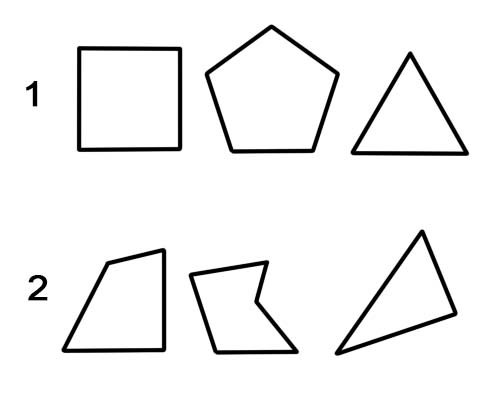
1. Regular na polygon.
2. Hindi regular na polygon.
Ang mga bilog at hugis na may kasamang mga kurba ay hindi mga polygon - isang polygon, ayon sa kahulugan, ay binubuo ng mga tuwid na linya.

Sa geometry, ang isang tatsulok ay isang sarado, dalawang-dimensional na hugis na may tatlong tuwid na linya. Ang tatsulok ay isa ring polygon.
Mahahanap natin ang hugis ng isang tatsulok sa isang bandila, isang signboard sa gilid ng kalsada at isang sandwich.
Ang isang tatsulok ay may tatlong gilid, tatlong vertice, at tatlong anggulo.
Ang kabuuan ng tatlong panloob na anggulo ng isang tatsulok ay palaging 180°. Ang kabuuan ng haba ng dalawang gilid ng isang tatsulok ay palaging mas malaki kaysa sa haba ng ikatlong panig.
Upang pag-uri-uriin ang mga tatsulok ayon sa kanilang mga anggulo, sinusukat namin ang bawat isa sa mga panloob na anggulo nito. Ang mga tatsulok ay maaaring uriin ayon sa mga anggulo, bilang:
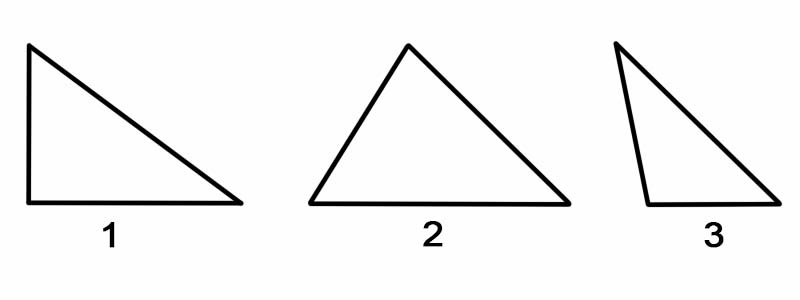
Upang pag-uri-uriin ang mga tatsulok ayon sa kanilang mga gilid, sinusukat namin ang haba ng bawat panig nito. Ang mga tatsulok ay maaaring uriin ayon sa kanilang mga panig, bilang:
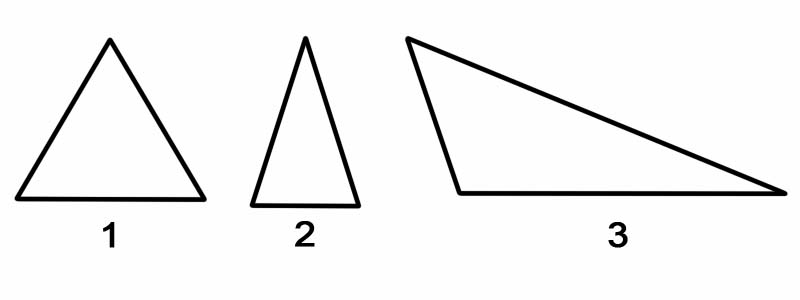
Tandaan: Ang isang tatsulok ay palaging maaaring hatiin sa dalawang kanang tatsulok, anuman ang oryentasyon nito.
Ang mga tatsulok ay mga polygon na may pinakamaliit na bilang ng mga gilid.
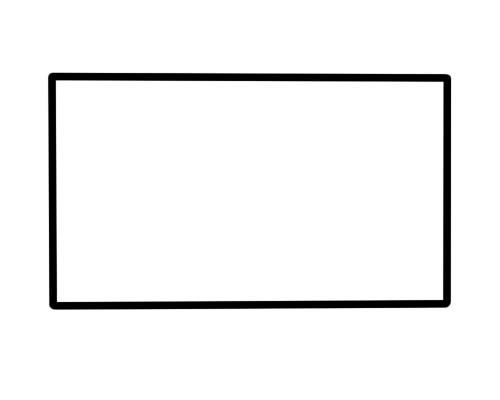
Ang parihaba ay isang hugis na may 4 na gilid, 4 na vertex, at 4 na anggulo. Ang magkabilang panig ay parallel at pantay ang haba. Lahat ng 4 na anggulo ay may sukat na 90 degrees.
Ang mga mesa, kahon, aklat, pinto, at papel ay parang mga parihaba.

Ang rhombus ay isang hugis na nabuo sa pamamagitan ng 4 na tuwid na linya. Ang 4 na gilid nito ay may parehong haba ngunit, hindi katulad ng parihaba, wala sa lahat ng 4 na anggulo ang may sukat na 90 degrees. Ang isang rhombus ay mukhang isang brilyante. Ang magkasalungat na panig ay magkatulad at magkatapat ang mga anggulo. Ang dalawang diagonal ng isang rhombus ay patayo sa isa't isa.

Ang isang parisukat ay isang dalawang-dimensional na pigura na ang lahat ng apat na panig ay pantay-pantay ang haba at ang dalawang magkasalungat na panig ay parallel sa isa't isa. Ito ay isang uri ng parihaba at rhombus (tinalakay sa ibaba). Ang 4 na panloob na anggulo ng isang parisukat ay 90º, o sa madaling salita, ang mga ito ay mga tamang anggulo. Kapag pinagsama-sama ang lahat ng mga anggulo, nagdaragdag sila ng hanggang 360º. Ang dalawang dayagonal na mayroon ang isang parisukat ay magkapareho ang haba at ang punto kung saan sila tumatawid ay ang sentro ng parisukat.
Tandaan: Ang parisukat ay palaging isang rhombus ngunit ang isang rhombus ay HINDI palaging isang parisukat. Kung ang bawat anggulo ng isang rhombus ay 90o, tanging ito ay isang parisukat.
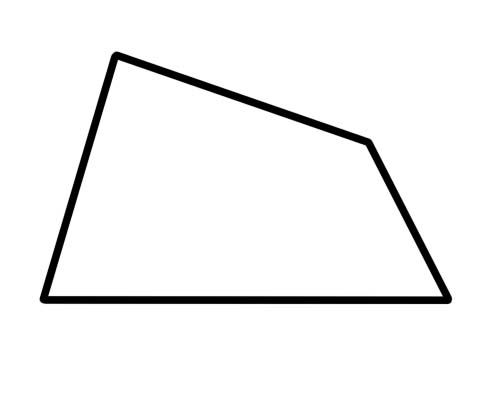
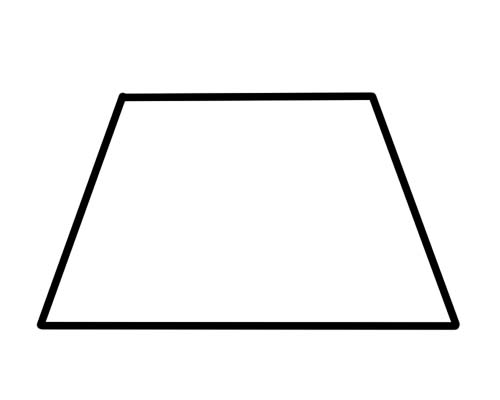
Ang trapezium ay isang may apat na gilid na may dalawang panig lamang na magkatulad.
Ayan yun. Walang mga panig na kailangang magkatugma (o magkapantay) at walang mga anggulo na kailangang magkatugma. Walang espesyal na nangyayari sa mga diagonal. Ang isang espesyal na uri ng trapezium ay ang 'isosceles trapezium' na may magkasalungat na gilid ng parehong haba at magkasalungat na anggulo ng parehong sukat. Ang mga diagonal ay pantay din ang haba.
Sa isang isosceles triangle, ang magkatabing mga anggulo sa mga gilid (ang mga anggulo sa tabi ng isa't isa) ay pandagdag. Nangangahulugan ito na nagdaragdag sila ng hanggang 180 degrees.
Ang trapezium ay hindi parallelogram dahil isang pares lamang ng magkasalungat na panig ang magkatulad.
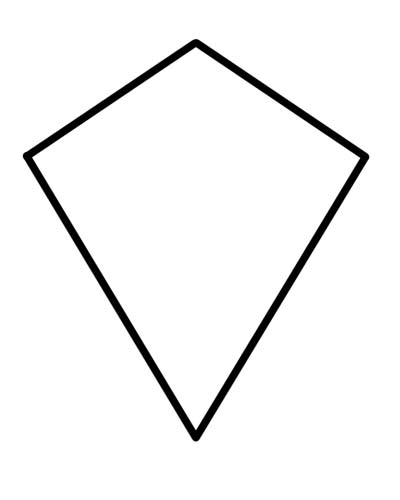
Ang saranggola ay isang quadrilateral na may eksaktong dalawang pares ng magkaparehong magkasunod na panig o kung saan ang dalawang magkahiwalay na pares ng magkasunod na panig ay magkatugma (ang ibig sabihin ng magkahiwalay na pares ay hindi magagamit ang isang panig sa parehong pares).
Kailangan mong malaman na ang bawat Rhombus ay isang saranggola, dahil ang Rhombus ay nasiyahan ang lahat ng mga katangian ng isang saranggola. Ang isang saranggola na may magkasalungat na panig ay tiyak na magiging isang rhombus. Kaya ang bawat Rhombus ay isang Saranggola ngunit hindi kabaliktaran. Ang saranggola ay hindi isang paralelogram dahil ang magkabilang panig ay hindi parallel sa isa't isa.
Quadrilaterals - Ang isang four-sided figure ay tinatawag na quadrilateral
Parallelogram - Ang parallelogram ay isang patag na hugis na may magkabilang panig na magkatulad at magkapareho ang haba.
Kaya, ang mga parihaba, parisukat, rhombus, trapezium at saranggola ay mga quadrilateral dahil mayroon silang apat na gilid bawat isa.
Gayunpaman, ang parihaba, parisukat at rhombus lamang ang mga paralelogram.
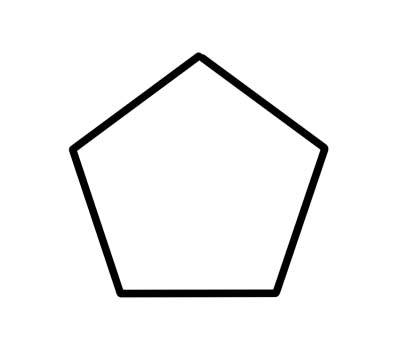
Ang Pentagon ay isang 5 panig na polygon na may limang panloob na anggulo na nagdaragdag sa 540 degrees. Ang mga regular na pentagon ay may magkaparehong haba ng mga gilid at ang bawat panloob na anggulo ay 108 degrees.
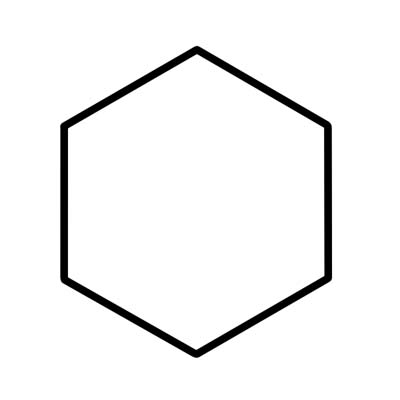
Ang Hexagon ay isang 6-sided polygon na may anim na panloob na anggulo na nagdaragdag sa 720 degrees. Ang hindi regular na hexagon ay may magkaibang haba ng mga gilid.
Ang isang regular na hexagon ay may magkaparehong haba ng mga gilid at ang bawat panloob na anggulo ay 120 degrees. Ang isang regular na hexagon ay binubuo ng anim na equilateral triangles na ang bawat gitnang anggulo ay katumbas ng 60 degrees.
[ipasok ang larawan: hexagon na nahahati sa anim na tatsulok at isang gitnang anggulo na may sukat na 60 degrees]
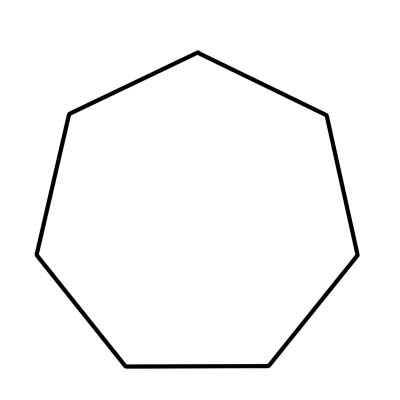
Ang heptagon ay isang pitong panig na polygon. Kasama ng pitong panig, ang isang heptagon ay may pitong vertice at anggulo. Ang lahat ng pitong panloob na anggulo ay nagdaragdag sa 900 degrees. Ang sukat ng bawat panloob na anggulo ng isang regular na heptagon ay humigit-kumulang 128.57 degrees o humigit-kumulang 129 degrees.
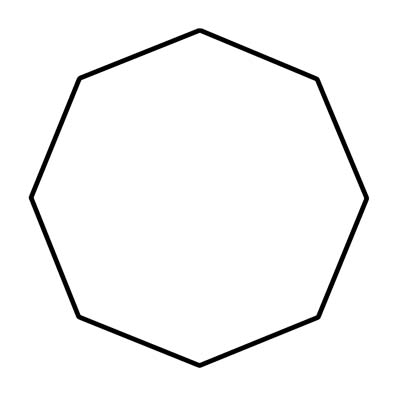
Ang octagon ay isang geometrical na hugis na naglalaman ng walong panig at walong anggulo. Ang mga oktagon ay dapat na may mga tuwid na gilid na kumokonekta; hindi sila maaaring hubog o idiskonekta. Madalas mong makikita ang mga octagon sa totoong buhay sa hugis ng isang stop sign. Ang sukat ng bawat isa sa walong panloob na anggulo ng isang regular na octagon ay humigit-kumulang 108 degrees. Ang isang matambok na octagon ay walang mga anggulo na nakaturo sa loob. Mas tiyak, walang panloob na mga anggulo ang maaaring higit sa 180°. Kapag ang anumang panloob na anggulo ay higit sa 180° ito ay malukong
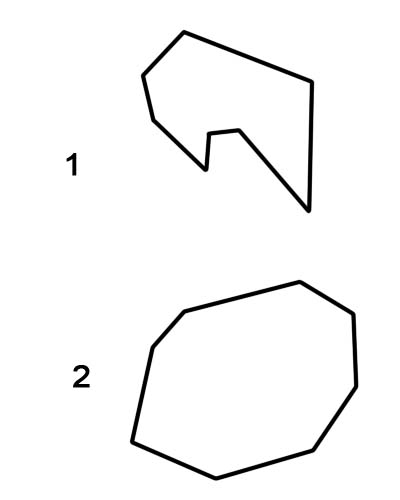
1. Malukong octagon
2. Matambok na octagon
Mahalagang tandaan na ang mga regular na octagon ay palaging inuuri bilang convex octagons, habang ang hindi regular na octagons ay maaaring maging concave o convex.
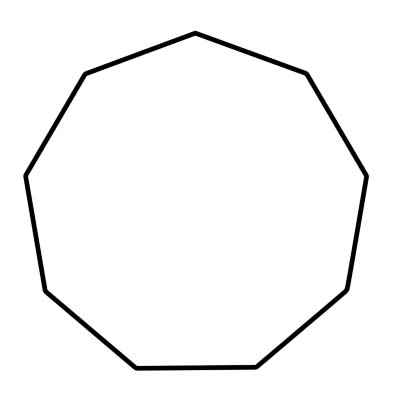
Ang nonagon ay isang polygon na may 9 na gilid at 9 na panloob na anggulo na nagdaragdag sa 1260 degrees. Ang isang regular na nonagon ay may lahat ng panig ng parehong haba at lahat ng panloob na mga anggulo ay may parehong laki. Ang sukat ng anggulo ng isang regular na nonagon ay 140 degrees. Ang nonagon ay binubuo ng 9 na tatsulok na may sukat ng bawat gitnang anggulo na katumbas ng 40 digri.
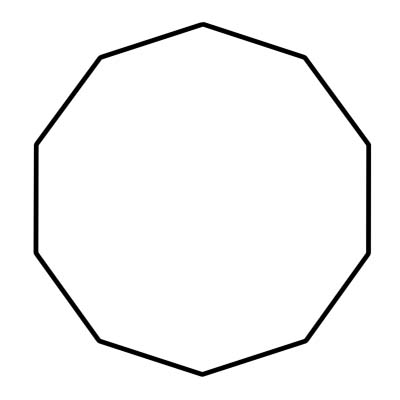
Ang decagon ay isang 10-panig na polygon. Mayroon din itong sampung vertices - kung saan nagtatagpo ang mga gilid - at mga anggulo. Ang kabuuan ng mga panloob na anggulo ng isang decagon ay 1440 degrees. Ang isang regular na decagon ay may magkaparehong panig at anggulo. Ang bawat anggulo ay may sukat na 144 degrees. Ang isang decagon ay binubuo ng 10 tatsulok na may gitnang anggulo na katumbas ng 36 degrees.
Ang mga hugis na maaaring masukat sa tatlong direksyon ay tinatawag na mga three-dimensional na hugis o 3D na hugis. Ang mga 3D na hugis ay tinatawag ding mga solidong hugis. Ang tatlong sukat ng mga 3D na hugis ay - Haba, lapad, at taas (o lalim o kapal).
Ang mga 3D na hugis ay iba sa mga 2D na hugis dahil mayroon silang kapal. Ang ilang mga halimbawa ng mga 3D na hugis mula sa ating pang-araw-araw na buhay ay:
Ang mga three-dimensional na hugis ay may mga vertice, mukha at mga gilid.
Ang prisma ay isang uri ng three-dimensional (3D) na hugis na may patag na gilid. Mayroon itong dalawang dulo na magkapareho ang hugis at sukat (at parang 2D na hugis). Ito ay may parehong cross-section kasama ang hugis mula sa dulo hanggang dulo; ibig sabihin, kapag pinutol mo ito, makikita mo ang parehong 2D na hugis sa magkabilang gilid.
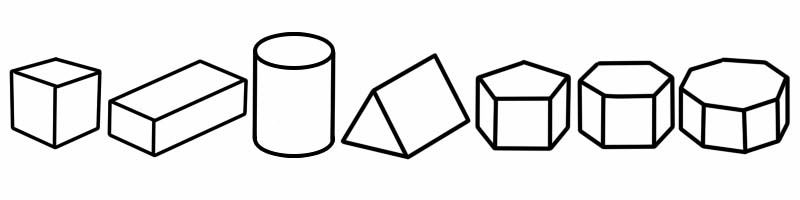
3D na Hugis | Bilang ng mga gilid | Bilang ng mga mukha | Bilang ng mga vertex |
Cube | 12 | 6 | 8 |
Kuboid | 12 | 6 | 8 |
Silindro | 2 | 3 | 0 |
Triangular na prisma | 9 | 5 (2 tatsulok, 3 parihaba) | 6 |
Pentagonal prism | 15 | 7 | 10 |
Hexagonal prism | 18 | 8 | 12 |
May walong sulok na prisma | 24 | 10 | 16 |
Ang pyramid ay isa ring three-dimensional (3D) na hugis. Ito ay may polygon base at patag (tatsulok) na mga gilid na nagsasama sa isang karaniwang punto (tinatawag na tuktok). Kapag binanggit ang salitang 'pyramid', ang unang pumapasok sa ating isipan ay ang mga sikat na pyramid ng Egypt. Ang Egyptian pyramids ay square-based pyramids, ngunit may ilang iba pang mga uri ng pyramids, bawat isa ay may ibang polygon bilang base nito.
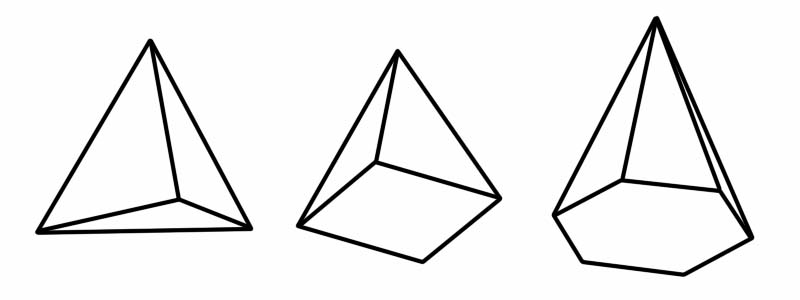
Hugis | Bilang ng mga gilid | Bilang ng mga mukha | Bilang ng mga vertex |
Tetrahedron | 6 | 4 | 4 |
Square pyramid | 8 | 5 | 5 |
Hexagonal pyramid | 12 | 7 | 7 |
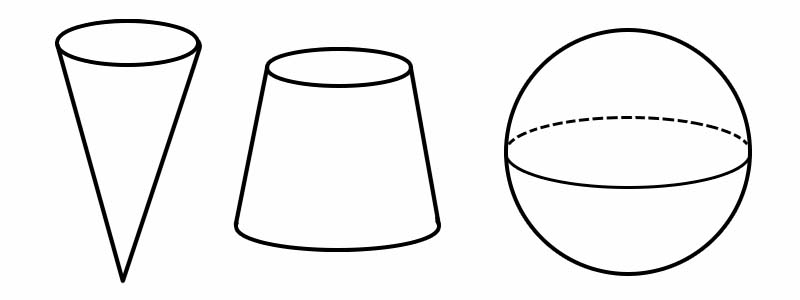
Hugis | Bilang ng mga gilid | Bilang ng mga mukha | Bilang ng mga vertex |
Kono | 1 | 2 | 1 |
Frustum | 2 | 3 | 0 |
Sphere | 0 | 1 | 0 |