Çevrenizdeki farklı nesneleri gözlemleyin. Çeşitli şekil ve boyutlarda gelirler. Bazıları aynı ve bazıları farklı. Tüm nesnelerin şekillerini tam olarak adlandıramasak da, matematikte büyük ölçüde 2B şekiller ve 3B şekillerden söz ederiz. Onlar hakkında daha fazlasını öğrenelim!
2B şekil kelimesi "iki boyutlu" bir şekli ifade eder. Yalnızca uzunluk ve genişlik olmak üzere iki boyutu olan geometrik bir şekil, 2 boyutlu bir şekildir. İki boyutlu şekillerin kalınlığı yoktur. Kenarlar düz veya eğri çizgilerden yapılmıştır. Herhangi bir sayıda kenara sahip olabilirler.
İki boyut kavramı, üzerinde her yere hareket edilebilecek düz bir yüzey olarak düşünülebilir. Düz yüzey düzlem olarak bilinir. 2B şekil, her zaman bir kağıt yaprağının üzerinde duran bir şeydir. Yüksekliği yoktur ve bu nedenle kağıt parçasının üzerine düşmez. 2B şekiller, düzlem şekiller veya düzlem şekiller olarak da bilinir.
2B şekillerin alanı vardır ancak hacmi yoktur.
Şekillerin özelliklerini özetlemek için üç önemli terim vardır:
Kenarlar - 2 boyutlu bir şekil üzerinde şekil oluşturan bir çizgi parçası.
Köşeler - Bir şeklin köşesi.
Açılar - Geometride açı, ortak bir uç noktada buluşan iki çizginin oluşturduğu şekil olarak tanımlanabilir.
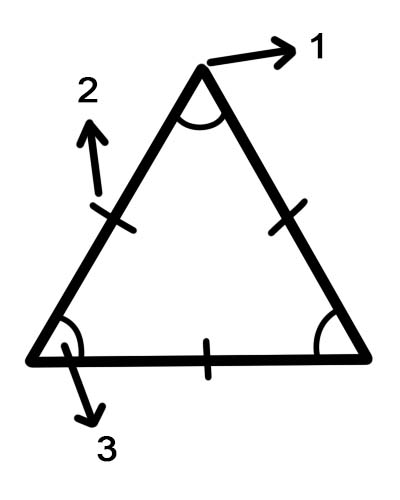
1. köşe
2. taraf
3. açılar
Farklı 2B şekilleri tartışalım.

Daire, köşeleri veya kenarları olmayan yuvarlak şekilli bir şekildir. Daire şeklini çevremizdeki bir araba lastiğinde, duvar saatinde ve bir lolipopta bulabiliriz. Bir dairenin merkezi, daire üzerindeki noktalara olan tüm mesafelerin eşit olduğu bir dairenin merkez noktasıdır. Merkezden daire üzerindeki herhangi bir noktaya olan uzaklığa yarıçap denir. Merkezden geçen daire boyunca olan mesafeyi düşünürsek, bu çaptır. Bir çemberin etrafındaki mesafeye çemberin çevresi denir.
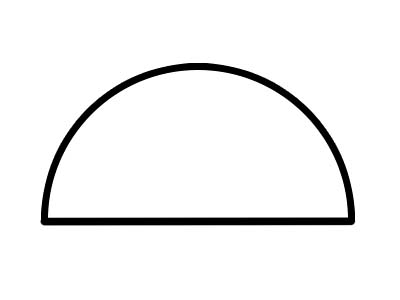
Yarım daire, yukarıda gösterildiği gibi bir çap çizgisi boyunca bütün bir dairenin kesilmesiyle oluşturulan yarım dairedir. Bir dairenin herhangi bir çapı onu iki eşit yarım daireye böler. Bir yarım dairenin tam yayı her zaman 180°'dir. Bir kurabiye ikiye bölünürse, her yarım bir yarım dairedir.

Oval, bir yumurtanın biçimine, şekline veya dış hatlarına sahiptir. Ovalin düz kenarları ve köşeleri yoktur, ancak izlenebilir veya bakıldığında düz bir şekil olarak görülebilen 1 yüzü vardır.
Çokgen, düz çizgileri olan bir düzlem şeklidir. Örnekler arasında üçgenler, dörtgenler, beşgenler, altıgenler vb. Düzgün bir çokgenin tüm kenarları ve tüm açıları eşittir. Aksi takdirde, düzensiz bir çokgendir.
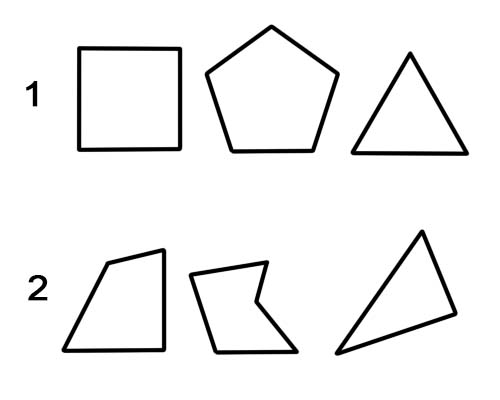
1. Normal çokgen.
2. Düzensiz çokgen.
Eğri içeren daireler ve şekiller çokgen değildir - çokgen, tanımı gereği düz çizgilerden oluşur.

Geometride üçgen, üç düz çizgiye sahip kapalı, iki boyutlu bir şekildir. Bir üçgen aynı zamanda bir çokgendir.
Üçgenin şeklini bir bayrakta, yol kenarındaki bir tabelada ve bir sandviçte bulabiliriz.
Bir üçgenin üç kenarı, üç köşesi ve üç açısı vardır.
Bir üçgenin üç iç açısının toplamı her zaman 180°'dir. Bir üçgende iki kenarın uzunlukları toplamı her zaman üçüncü kenarın uzunluğundan büyüktür.
Üçgenleri açılarına göre sınıflandırmak için her birinin iç açılarını ölçeriz. Üçgenler açılarına göre şu şekilde sınıflandırılabilir:
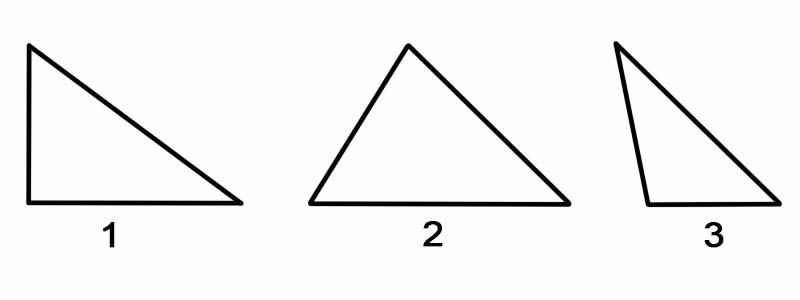
Üçgenleri kenarlarına göre sınıflandırmak için her bir kenarının uzunluğunu ölçeriz. Üçgenler kenarlarına göre şu şekilde sınıflandırılabilir:
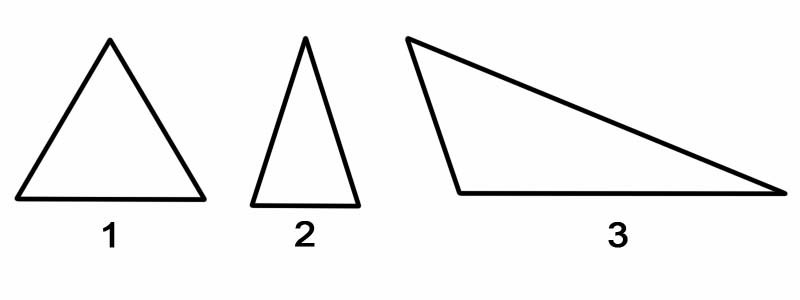
Unutmayın: Yönünden bağımsız olarak bir üçgen her zaman iki dik üçgene bölünebilir.
Üçgenler, kenar sayısı en az olan çokgenlerdir.
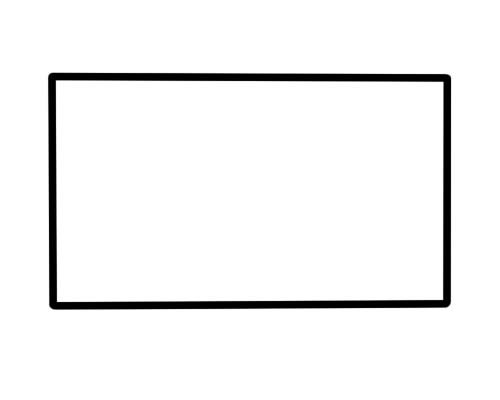
Dikdörtgen, 4 kenarı, 4 köşesi ve 4 açısı olan bir şekildir. Karşılıklı kenarlar paralel ve uzunlukları eşittir. 4 açısı da 90 derecedir.
Masalar, kutular, kitaplar, kapılar ve kağıtlar dikdörtgen gibi görünür.

Eşkenar dörtgen 4 düz çizgiden oluşan bir şekildir. 4 kenarı aynı uzunluktadır, ancak dikdörtgenin aksine, 4 açısının hiçbiri 90 dereceyi ölçmez. Bir eşkenar dörtgen bir elmas gibi görünür. Karşılıklı kenarlar paralel ve karşılıklı açılar eşittir. Bir eşkenar dörtgenin iki köşegeni birbirine diktir.

Kare, dört kenarı da eşit uzunlukta ve karşılıklı iki kenarı birbirine paralel olan iki boyutlu bir şekildir. Bir tür dikdörtgen ve eşkenar dörtgendir (aşağıda tartışılmıştır). Karenin 4 iç açısı da 90 derecedir yani dik açıdır. Tüm açılar toplandığında 360º'yi bulur. Karenin iki köşegeninin uzunlukları birbirine eşittir ve kesiştikleri nokta karenin merkezidir.
Unutmayın: Kare her zaman eşkenar dörtgendir, ancak eşkenar dörtgen her zaman kare DEĞİLDİR. Bir eşkenar dörtgenin her açısı 90° ise, ancak o zaman o bir karedir.
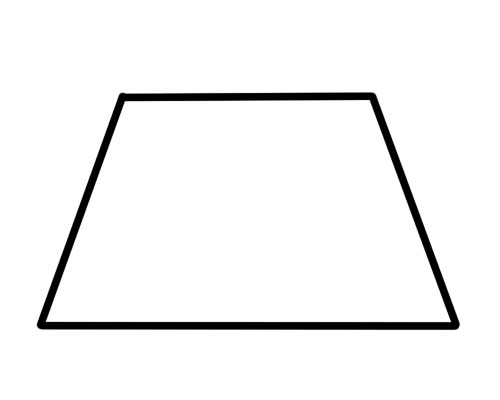
Yamuk, yalnızca iki kenarı paralel olan bir dörtgendir.
Bu kadar. Hiçbir kenarın uyumlu (veya eşit) olması ve hiçbir açının uyumlu olması gerekmez. Köşegenlerde özel bir şey olmaz. Özel bir yamuk türü, karşılıklı kenarları aynı uzunlukta ve zıt açıları aynı ölçüde olan 'ikizkenar yamuktur'. Köşegenler de eşit uzunluktadır.
Bir ikizkenar üçgende, kenarlar boyunca bitişik açılar (yan yana olan açılar) tümler. Bu, 180 dereceye kadar topladıkları anlamına gelir.
Yamuk bir paralelkenar değildir, çünkü yalnızca bir çift karşılıklı kenar paraleldir.
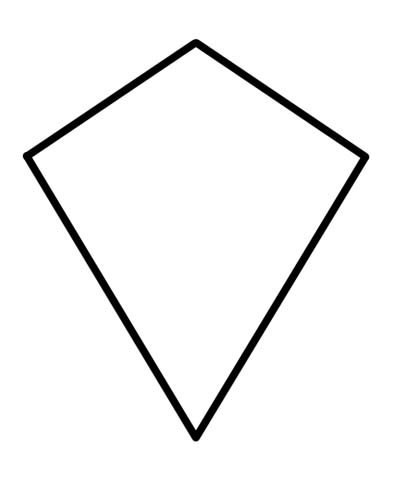
Uçurtma, tam olarak iki çift eşit ardışık kenara sahip veya iki ayrık ardışık kenar çiftinin uyumlu olduğu bir dörtgendir (ayrık çiftler, bir tarafın her iki çiftte kullanılamayacağı anlamına gelir).
Rhombus bir uçurtmanın tüm özelliklerini karşıladığı için her Rhombus'un bir uçurtma olduğunu bilmelisiniz. Karşılıklı kenarları paralel olan bir uçurtma kesinlikle eşkenar dörtgen olur. Bu nedenle, her Rhombus bir Uçurtmadır, ancak tersi değildir. Karşılıklı kenarlar birbirine paralel olmadığı için uçurtma paralelkenar değildir.
Dörtgenler - Dört kenarlı bir şekle dörtgen denir
Paralelkenar - Paralelkenar, karşılıklı kenarları paralel ve eşit uzunlukta olan düz bir şekildir.
Böylece, dikdörtgen, kare, eşkenar dörtgen, yamuk ve uçurtma şekilleri, her birinin dört kenarı olduğu için dörtgendir.
Ancak, yalnızca dikdörtgen, kare ve eşkenar dörtgen paralelkenardır.
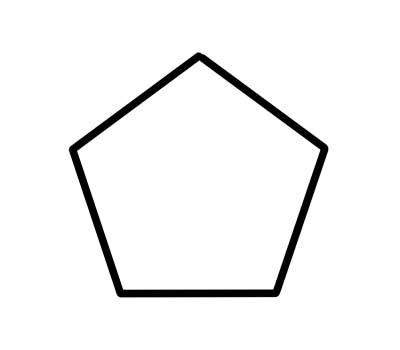
Beşgen, toplamı 540 derece olan beş iç açısı olan 5 kenarlı bir çokgendir. Düzgün beşgenlerin kenar uzunlukları birbirine eşittir ve her bir iç açısı 108 derecedir.
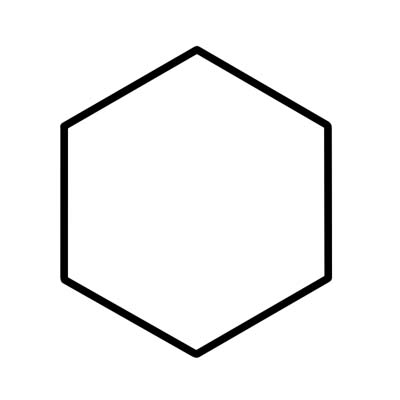
Altıgen, toplamı 720 derece olan altı iç açısı olan 6 kenarlı bir çokgendir. Düzensiz altıgenin farklı uzunluklarda kenarları vardır.
Düzgün bir altıgenin kenarları eşit uzunluktadır ve her bir iç açısı 120 derecedir. Düzgün bir altıgen, her biri 60 dereceye eşit olan altı eşkenar üçgenden oluşur.
[resmi ekleyin: altı üçgene bölünmüş altıgen ve 60 derecelik bir merkez açı]
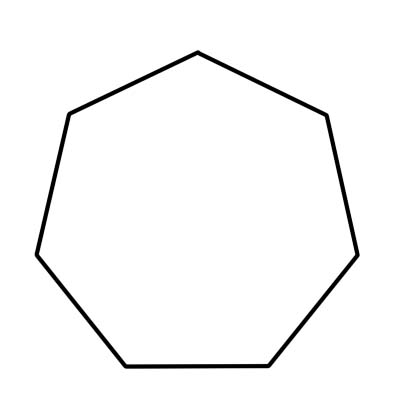
Bir yedigen, yedi kenarlı bir çokgendir. Yedi kenarın yanı sıra, bir yedigenin yedi köşesi ve açısı vardır. Yedi iç açının tümü toplamı 900 derecedir. Düzgün bir yedigenin her bir iç açısının ölçüsü yaklaşık 128,57 derece veya yaklaşık 129 derecedir.
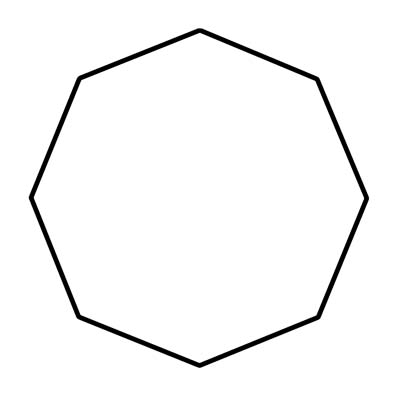
Sekizgen, sekiz kenarı ve sekiz açısı olan geometrik bir şekildir. Sekizgenlerin birbirine bağlanan düz kenarları olmalıdır; kavisli veya bağlantısız olamazlar. Sekizgenleri gerçek hayatta sık sık dur işareti şeklinde görürsünüz. Bir düzgün sekizgenin sekiz iç açısının her birinin ölçüsü yaklaşık 108 derecedir. Dışbükey bir sekizgenin içe dönük açıları yoktur. Daha doğrusu, hiçbir iç açı 180°'den fazla olamaz. Herhangi bir iç açı 180°'den büyük olduğunda içbükeydir
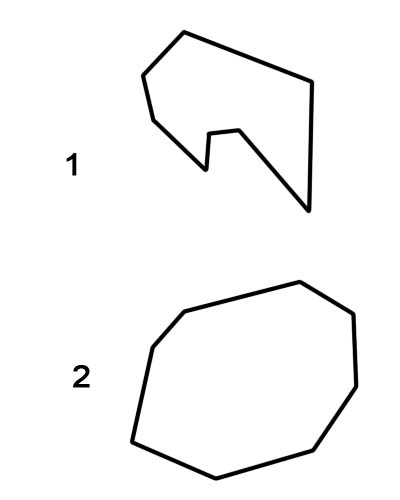
1. İçbükey sekizgen
2. Dışbükey sekizgen
Düzenli sekizgenlerin her zaman dışbükey sekizgenler olarak sınıflandırıldığına, düzensiz sekizgenlerin ise içbükey veya dışbükey olabileceğine dikkat etmek önemlidir.
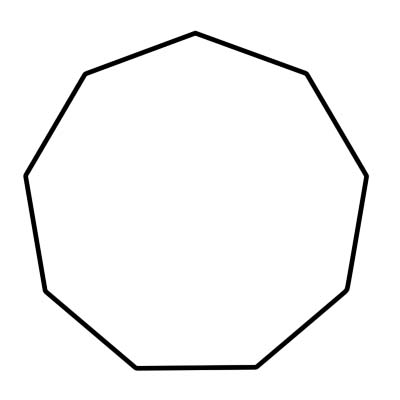
Bir dokuzgen, 9 kenarı ve 9 iç açısı olan ve toplamı 1260 derece olan bir çokgendir. Düzgün bir dokuzgenin tüm kenarları aynı uzunluktadır ve tüm iç açıları aynı boyuttadır. Düzgün bir dokuzgenin iç açısının ölçüsü 140 derecedir. Bir dokuzgen, her bir merkez açının ölçüsü 40 dereceye eşit olan 9 üçgenden oluşur.
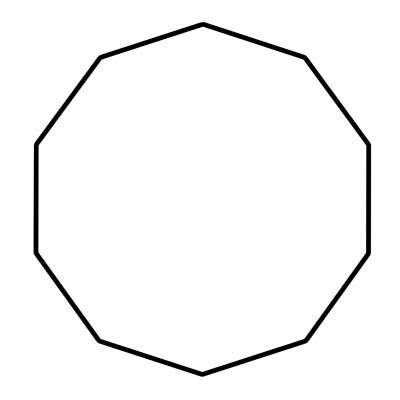
Bir ongen, 10 kenarlı bir çokgendir. Ayrıca kenarların birleştiği yer olan on köşesi ve açıları vardır. Bir ongenin iç açıları toplamı 1440 derecedir. Düzenli bir ongen, uyumlu kenarlara ve açılara sahiptir. Her bir açısı 144 derecedir. Bir ongen, merkez açıları 36 dereceye eşit olan 10 üçgenden oluşur.
Üç yönde ölçülebilen şekillere üç boyutlu şekiller veya 3 boyutlu şekiller denir. 3B şekillere katı şekiller de denir. 3B şekillerin üç ölçümü şunlardır: - Uzunluk, genişlik ve yükseklik (veya derinlik veya kalınlık).
3B şekiller, kalınlıkları nedeniyle 2B şekillerden farklıdır. Günlük yaşamımızdan bazı 3B şekil örnekleri:
Üç boyutlu şekillerin köşeleri, yüzleri ve kenarları vardır.
Prizma, düz kenarları olan bir tür üç boyutlu (3B) şekildir. Aynı şekil ve boyutta (ve 2B şekle benzeyen) iki ucu vardır. Boydan boya aynı enine kesite sahiptir; bu, keserseniz her iki tarafta da aynı 2B şekli göreceğiniz anlamına gelir.
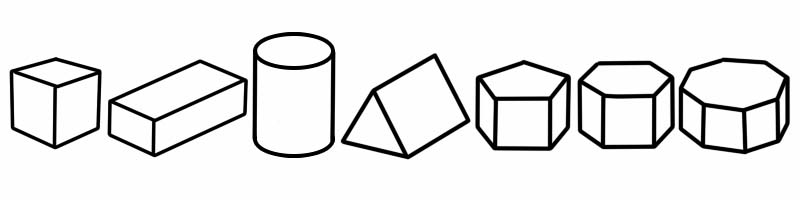
3B Şekil | kenar sayısı | yüz sayısı | köşe sayısı |
Küp | 12 | 6 | 8 |
küboid | 12 | 6 | 8 |
silindir | 2 | 3 | 0 |
Üçgen prizma | 9 | 5 (2 üçgen, 3 dikdörtgen) | 6 |
beşgen prizma | 15 | 7 | 10 |
altıgen prizma | 18 | 8 | 12 |
sekizgen prizma | 24 | 10 | 16 |
Bir piramit aynı zamanda üç boyutlu (3B) bir şekildir. Çokgen bir tabana ve ortak bir noktada (tepe olarak adlandırılan) birleşen düz (üçgen) kenarlara sahiptir. Piramit denilince aklımıza ilk olarak Mısır'ın meşhur piramitleri gelir. Mısır piramitleri kare tabanlı piramitlerdir, ancak her birinin tabanı farklı bir çokgen olan başka piramit türleri de vardır.
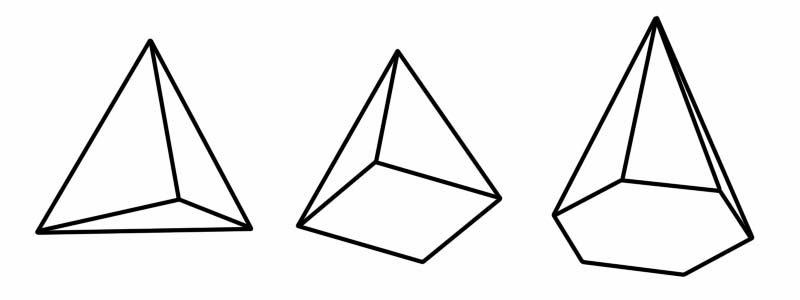
Şekil | kenar sayısı | yüz sayısı | köşe sayısı |
dörtyüzlü | 6 | 4 | 4 |
Kare piramit | 8 | 5 | 5 |
altıgen piramit | 12 | 7 | 7 |
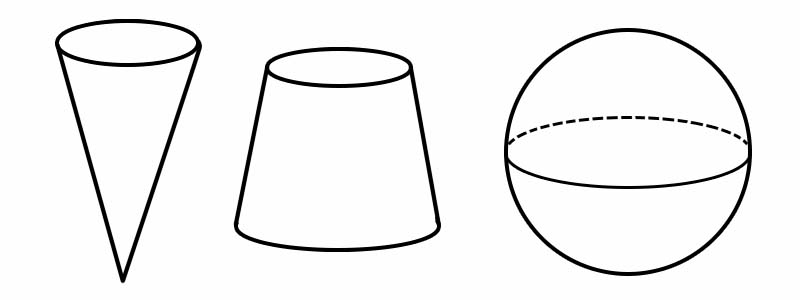
Şekil | kenar sayısı | yüz sayısı | köşe sayısı |
koni | 1 | 2 | 1 |
Frustum | 2 | 3 | 0 |
Küre | 0 | 1 | 0 |