Спостерігайте за різними предметами навколо вас. Вони бувають різних форм і розмірів. Деякі однакові, а деякі різні. Хоча ми не можемо точно назвати форми всіх об’єктів, у математиці ми в основному говоримо про 2D-форми та 3D-форми. Давайте дізнаємося про них більше!
Слово 2D-форма відноситься до «двовимірної» форми. Геометрична фігура, яка має два виміри – лише довжину та ширину, є двовимірною формою. Двовимірні форми не мають товщини. Борти виконуються прямими або кривими лініями. Вони можуть мати будь-яку кількість сторін.
Концепцію двох вимірів можна розглядати як плоску поверхню, на якій можна рухатися куди завгодно. Плоска поверхня називається площиною. 2D фігура – це те, що завжди лежить на аркуші паперу. Він не має висоти, а тому не падає над аркушем паперу. Двовимірні форми також відомі як плоскі форми або плоскі фігури.
2D-фігури мають площу, але не мають об’єму.
Є три важливі терміни для окреслення характеристик форм:
Сторони – відрізок лінії, який утворює фігуру на двовимірній фігурі.
Вершини - кут фігури.
Кути - в геометрії кут можна визначити як фігуру, утворену двома лініями, що зустрічаються в спільній кінцевій точці.
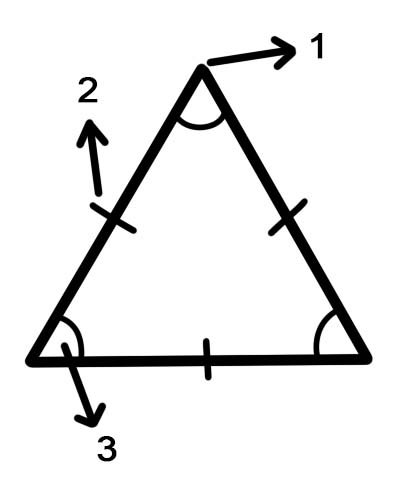
1. вершина
2. сторони
3.кути
Давайте обговоримо різні двовимірні форми.

Коло — це фігура круглої форми, яка не має кутів і країв. Ми можемо знайти форму кола в автомобільній шині, настінному годиннику та льодянику навколо нас. Центр кола - це центральна точка кола, від якої всі відстані до точок кола рівні. Відстань від центра до будь-якої точки кола називається радіусом. Якщо ми розглядаємо відстань через коло, що проходить через центр, це діаметр. Відстань навколо кола називається довжиною кола.
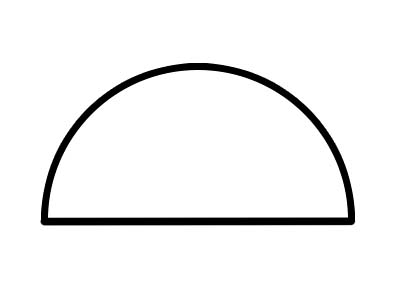
Півколо — це півколо, утворене розрізанням цілого кола по лінії діаметра, як показано вище. Будь-який діаметр кола розрізає його на два рівних півкола. Повна дуга півкола завжди має кут 180°. Якщо печиво розрізати на дві половинки, то кожна половинка є півколом.

Овал має форму, форму або контур яйця. Овал не має прямих сторін і кутів, але він має 1 грань, яку можна простежити або побачити як плоску форму, дивлячись на неї.
Багатокутник — це плоска фігура з прямими лініями. Приклади включають трикутники, чотирикутники, п'ятикутники, шестикутники тощо. У правильного многокутника всі сторони рівні і всі кути рівні. В іншому випадку це неправильний многокутник.
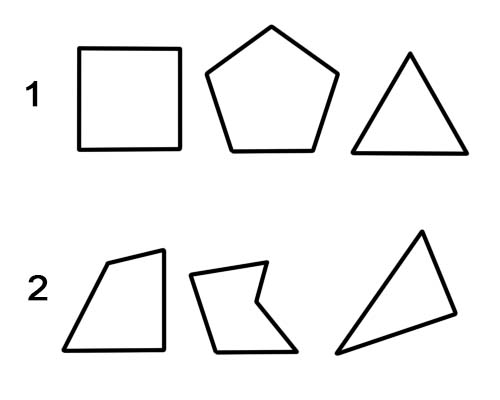
1. Правильний многокутник.
2. Неправильний многокутник.
Кола та фігури, які містять криві, не є багатокутниками – багатокутник, за визначенням, складається з прямих ліній.

У геометрії трикутник — замкнута двовимірна фігура з трьома прямими лініями. Трикутник також є багатокутником.
Форму трикутника ми можемо зустріти на прапорі, придорожньому покажчику та бутерброді.
Трикутник має три сторони, три вершини і три кути.
Сума трьох внутрішніх кутів трикутника завжди дорівнює 180°. Сума довжин двох сторін трикутника завжди більша за довжину третьої сторони.
Щоб класифікувати трикутники за їхніми кутами, ми виміряємо кожен із його внутрішніх кутів. Трикутники можна класифікувати за кутами, як:
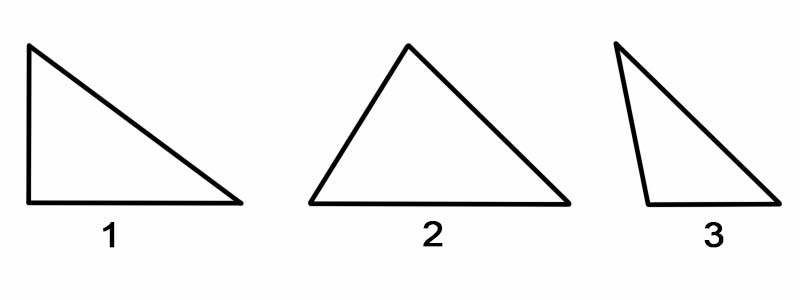
Щоб класифікувати трикутники за їх сторонами, ми виміряємо довжину кожної з його сторін. За сторонами трикутники можна класифікувати так:
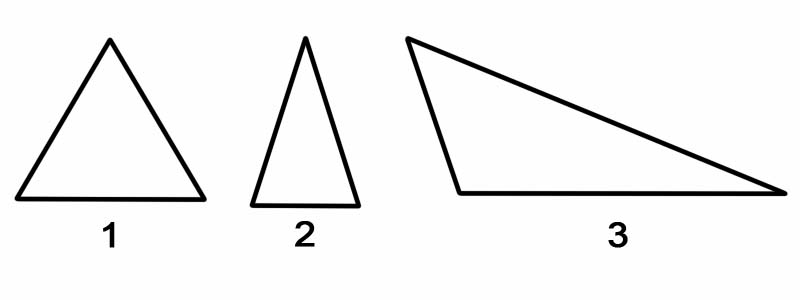
Пам’ятайте: трикутник завжди можна розбити на два прямокутних трикутника, незалежно від його орієнтації.
Трикутники - це багатокутники з найменшою кількістю сторін.
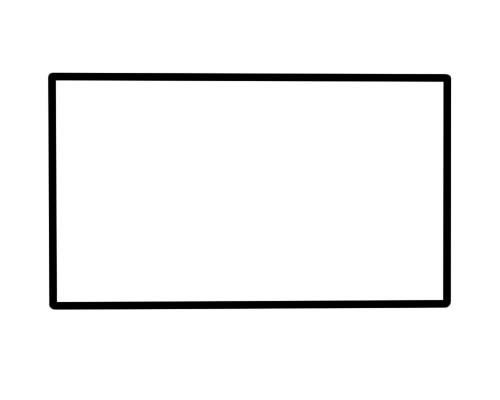
Прямокутник - це фігура, яка має 4 сторони, 4 вершини і 4 кути. Протилежні сторони паралельні й однакові за довжиною. Усі 4 кути мають 90 градусів.
Столи, ящики, книги, двері, папір виглядають як прямокутники.

Ромб — фігура, утворена 4 прямими лініями. Його 4 сторони мають однакову довжину, але, на відміну від прямокутника, жоден із 4 кутів не має 90 градусів. Ромб схожий на ромб. Протилежні сторони паралельні, а протилежні кути рівні. Дві діагоналі ромба перпендикулярні одна до одної.

Квадрат — це двовимірна фігура, усі чотири сторони якої мають однакову довжину, а дві протилежні сторони паралельні одна одній. Це різновид прямокутника та ромба (розглянемо нижче). 4 внутрішні кути квадрата дорівнюють 90º, або іншими словами, вони прямі кути. Коли всі кути додаються разом, вони дають 360º. Дві діагоналі квадрата мають однакову довжину, і точка, де вони перетинаються, є центром квадрата.
Пам’ятайте: квадрат – це завжди ромб, але ромб – НЕ завжди квадрат. Якщо кожен кут ромба дорівнює 90°, то це квадрат.
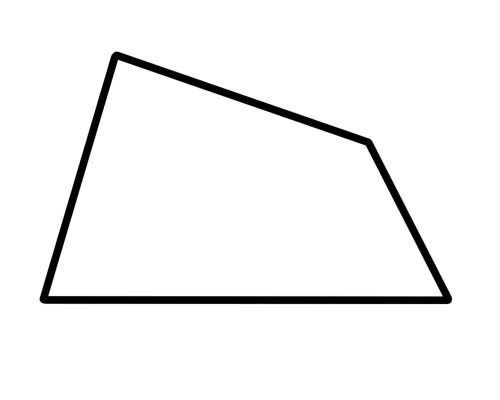
Трапеція - це чотирикутник, лише дві сторони якого паралельні.
Це воно. Жодна сторона не повинна бути конгруентною (або рівною), а жодні кути не повинні бути рівними. З діагоналями нічого особливого не відбувається. Особливим типом трапеції є «рівнобедрена трапеція», яка має протилежні сторони однакової довжини та протилежні кути однакової міри. Діагоналі також мають однакову довжину.
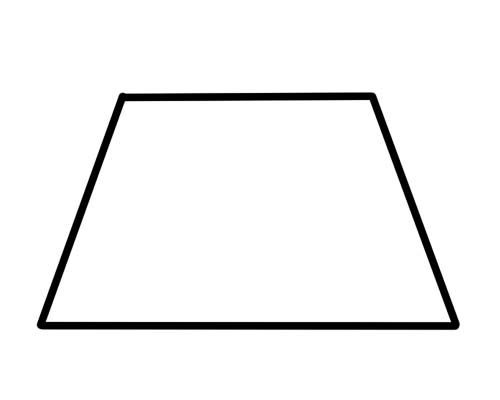
У рівнобедреному трикутнику суміжні кути вздовж бічних сторін (кути один біля одного) є додатковими. Це означає, що вони складаються до 180 градусів.
Трапеція не є паралелограмом, оскільки лише одна пара протилежних сторін паралельна.
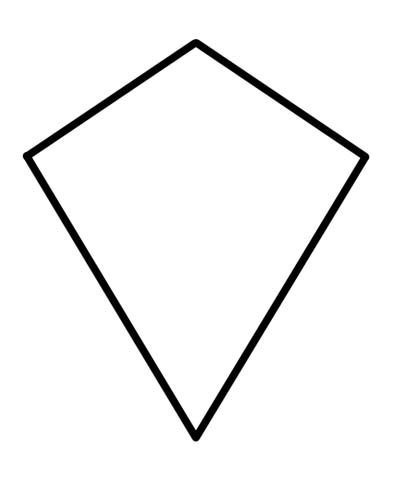
Повітряний змій — це чотирикутник із двома парами рівних послідовних сторін або в якому дві непересічні пари послідовних сторін є рівними (непересічні пари означають, що одна сторона не може використовуватися в обох парах).
Потрібно знати, що кожен ромб є повітряним змієм, тому що ромб має всі властивості повітряного змія. Повітряний змій з паралельними протилежними сторонами однозначно стає ромбом. Таким чином, кожен ромб є повітряним змієм, але не навпаки. Повітряний змій не є паралелограмом, оскільки протилежні сторони не паралельні одна одній.
Чотирикутники – Чотирикутником називають чотиригранну фігуру
Паралелограм - Паралелограм - це плоска форма з протилежними сторонами, паралельними та однаковими за довжиною.
Таким чином, прямокутник, квадрат, ромб, трапеція та повітряний змій є чотирикутниками, оскільки вони мають по чотири сторони.
Але тільки прямокутник, квадрат і ромб є паралелограмами.
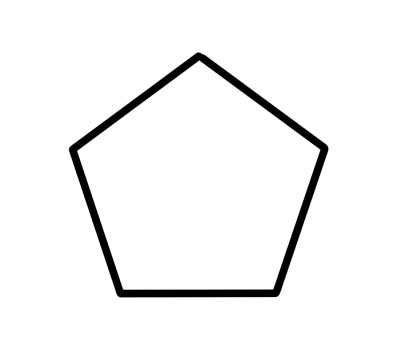
П'ятикутник - це 5-гранний багатокутник із п'ятьма внутрішніми кутами, які в сумі становлять 540 градусів. Правильні п'ятикутники мають однакову довжину сторін і кожен внутрішній кут дорівнює 108 градусів.
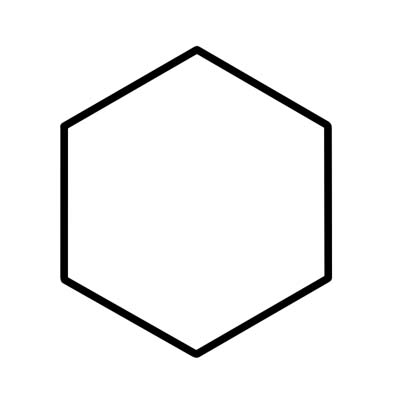
Шестикутник — це 6-сторонній багатокутник із шістьма внутрішніми кутами, що додають 720 градусів. Неправильний шестикутник має сторони різної довжини.
Правильний шестикутник має однакову довжину сторін і кожен внутрішній кут дорівнює 120 градусів. Правильний шестикутник складається з шести рівносторонніх трикутників, кожен з яких дорівнює 60 градусам.
[вставте зображення: шестикутник, поділений на шість трикутників і один центральний кут розміром 60 градусів]
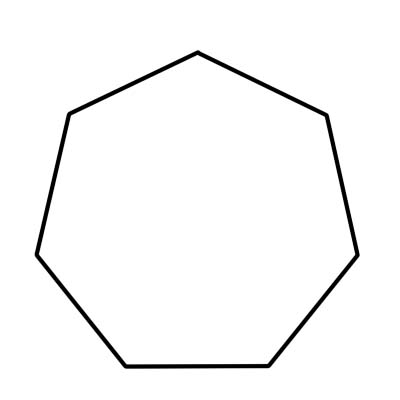
Семикутник - це семикутник. Разом із сімома сторонами семикутник має сім вершин і кутів. Усі сім внутрішніх кутів додають 900 градусів. Міра кожного внутрішнього кута правильного семикутника становить приблизно 128,57 градусів або приблизно 129 градусів.
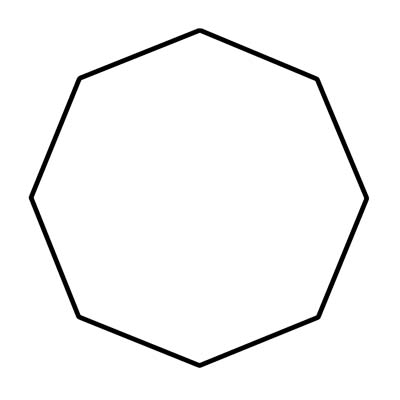
Восьмикутник - це геометрична фігура, яка містить вісім сторін і вісім кутів. Восьмикутники повинні мати прямі сторони, які з’єднуються; їх неможливо викривити або роз'єднати. У реальному житті ви часто побачите восьмикутники у формі знака «стоп». Розмір кожного з восьми внутрішніх кутів правильного восьмикутника дорівнює приблизно 108 градусам. Опуклий восьмикутник не має кутів, спрямованих всередину. Точніше, жоден внутрішній кут не може бути більше 180°. Коли будь-який внутрішній кут перевищує 180°, він увігнутий
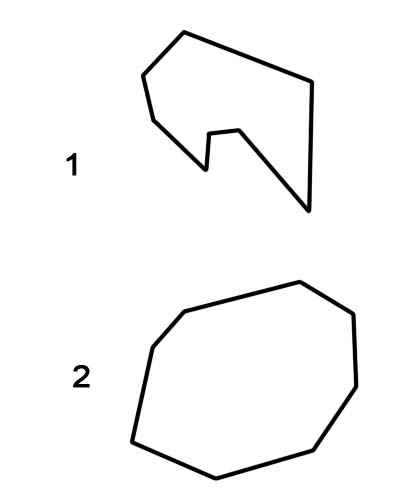
1. Увігнутий восьмикутник
2. Опуклий восьмикутник
Важливо відзначити, що правильні восьмикутники завжди класифікуються як опуклі восьмикутники, тоді як неправильні восьмикутники можуть бути увігнутими або опуклими.
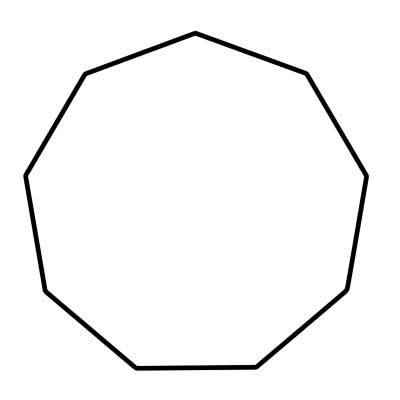
Нонакутник - це багатокутник з 9 сторонами і 9 внутрішніми кутами, які в сумі становлять 1260 градусів. Правильний некутник має всі сторони однакової довжини і всі внутрішні кути однакової величини. Міра кута правильного некутника дорівнює 140 градусів. Нонакутник складається з 9 трикутників, центральний кут яких дорівнює 40 градусам.
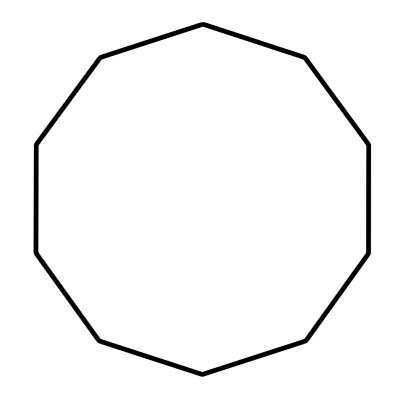
Десятикутник - це 10-гранний многокутник. Він також має десять вершин, де зустрічаються сторони, і кути. Сума внутрішніх кутів десятикутника дорівнює 1440 градусів. Правильний десятикутник має рівні сторони та кути. Кожен кут має 144 градуси. Десятикутник складається з 10 трикутників, центральний кут яких дорівнює 36 градусам.
Фігури, які можна вимірювати в трьох напрямках, називаються тривимірними або тривимірними фігурами. Тривимірні фігури також називають твердими фігурами. Тривимірні форми тривимірні: довжина, ширина та висота (або глибина чи товщина).
3D-форми відрізняються від 2D-форм, оскільки вони мають товщину. Деякі приклади тривимірних форм із нашого повсякденного життя:
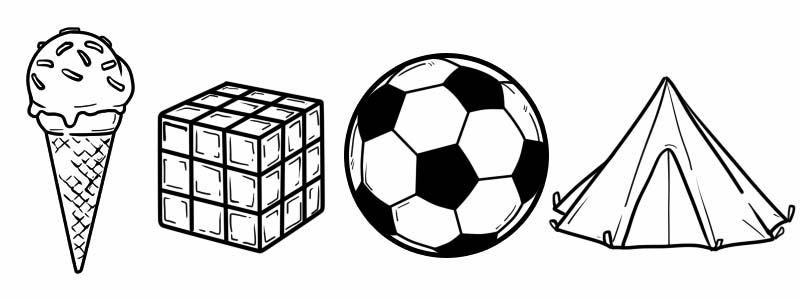
Тривимірні фігури мають вершини, грані та ребра.
Призма — це тип тривимірної (3D) форми з плоскими сторонами. Він має два кінці однакової форми та розміру (і виглядають як 2D-форма). Він має однаковий поперечний переріз і форму від кінця до кінця; це означає, що якщо ви його розріжете, ви побачите ту саму двовимірну форму, що й з обох сторін.
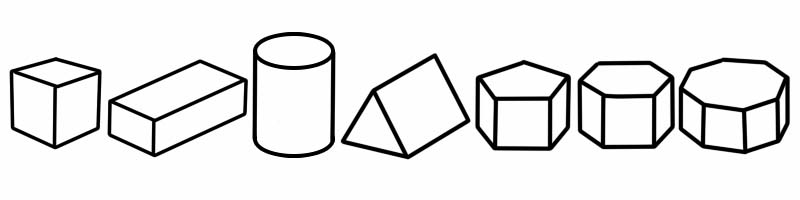
3D форма | Кількість ребер | Кількість граней | Кількість вершин |
куб | 12 | 6 | 8 |
Кубоподібний | 12 | 6 | 8 |
Циліндр | 2 | 3 | 0 |
Трикутна призма | 9 | 5 (2 трикутники, 3 прямокутники) | 6 |
П'ятикутна призма | 15 | 7 | 10 |
Шестикутна призма | 18 | 8 | 12 |
Восьмикутна призма | 24 | 10 | 16 |
Піраміда також є тривимірною (3D) формою. Він має багатокутну основу та плоскі (трикутні) сторони, які з’єднуються в спільній точці (яка називається вершиною). Коли згадується слово «піраміда», перше, що спадає на думку, це знамениті піраміди Єгипту. Єгипетські піраміди мають квадратну основу, але існує кілька інших типів пірамід, кожна з яких має окремий багатокутник як основу.
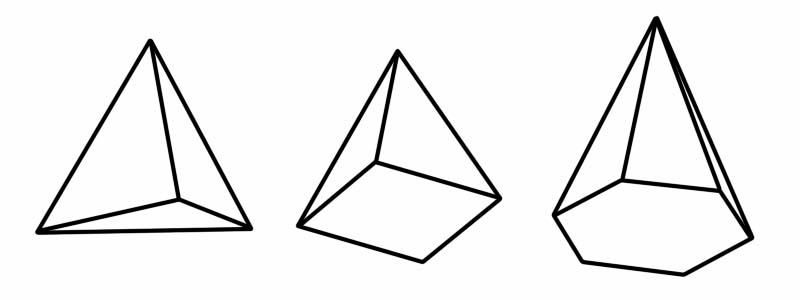
Форма | Кількість ребер | Кількість граней | Кількість вершин |
Тетраедр | 6 | 4 | 4 |
Квадратна піраміда | 8 | 5 | 5 |
Шестикутна піраміда | 12 | 7 | 7 |
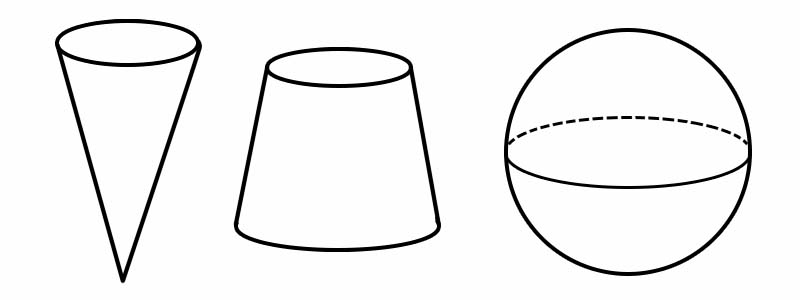
Форма | Кількість ребер | Кількість граней | Кількість вершин |
Конус | 1 | 2 | 1 |
Усічений | 2 | 3 | 0 |
Сфера | 0 | 1 | 0 |