اپنے آس پاس کی مختلف اشیاء کو دیکھیں۔ وہ مختلف شکلیں اور سائز میں آتے ہیں۔ کچھ ایک جیسے ہیں اور کچھ مختلف ہیں۔ اگرچہ ہم تمام چیزوں کی شکل کا واضح طور پر نام نہیں لے سکتے ہیں ، لیکن ریاضی میں ہم بڑے پیمانے پر 2D شکلوں اور 3D شکلوں کے بارے میں بات کرتے ہیں۔ آئیے ان کے بارے میں مزید جانیں!
2D شکل لفظ سے مراد "دو جہتی" شکل ہے۔ ایک ہندسی اعداد و شمار جس میں دو جہت ہیں - لمبائی اور چوڑائی صرف 2 ڈی شکل ہوتی ہے۔ دو جہتی شکلوں کی کوئی موٹائی نہیں ہے۔ اطراف سیدھے یا مڑے ہوئے لکیروں سے بنے ہیں۔ ان کے اطراف کی تعداد بہت ہوسکتی ہے۔
دو جہتوں کا تصور ایک فلیٹ سطح کے طور پر سوچا جاسکتا ہے جس پر کوئی کہیں بھی حرکت کرنے کے قابل ہوتا ہے۔ فلیٹ سطح کو ہوائی جہاز کے نام سے جانا جاتا ہے۔ 2 ڈی شکل ایسی چیز ہے جو ہمیشہ کاغذ کی شیٹ پر پڑتی ہے۔ اس کی اونچائی نہیں ہے ، اور اسی وجہ سے یہ کاغذ کے ٹکڑے سے اوپر نہیں آتا ہے۔ 2 ڈی شکلیں ہوائی جہاز کی شکل یا ہوائی جہاز کے اعداد و شمار کے طور پر بھی جانا جاتا ہے۔
2 ڈی شکلوں کا رقبہ ہے لیکن حجم نہیں ہے۔
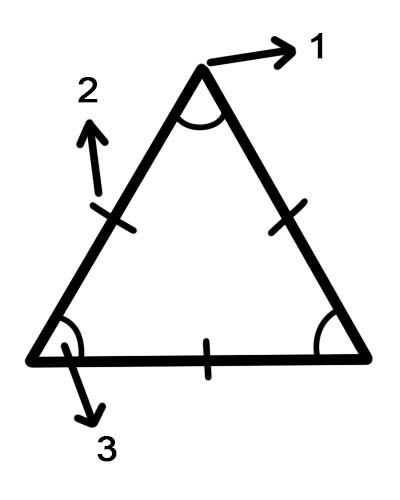
اشکال کی خصوصیات کا خاکہ پیش کرنے کے لئے تین اہم شرائط ہیں۔
سائیڈز - ایک لائن طبقہ جو 2 جہتی شخصیت پر شکل بناتا ہے۔
Vertices - اعداد و شمار کا ایک کونہ۔
زاویے - جیومیٹری میں ، ایک زاویہ کی وضاحت اس اعداد و شمار کے طور پر کی جاسکتی ہے جو مشترکہ اختتامی نقطہ پر دو لائنوں سے مل کر تشکیل پاتا ہے۔
1. شہد
2. اطراف
3. بنگلے
آئیے مختلف 2D شکلوں پر تبادلہ خیال کرتے ہیں۔

حلقہ ایک گول شکل کی شکل ہے جس کے کونے یا کنارے نہیں ہیں۔ ہم اپنے آس پاس کار کے ٹائر ، دیوار گھڑی اور لالی چپ میں دائرہ کی شکل پاسکتے ہیں۔ دائرے کا مرکز ایک دائرے میں مرکزی نقطہ ہوتا ہے ، جہاں سے دائرے کے نقطہ تک تمام فاصلے برابر ہوتے ہیں۔ دائرے میں کسی بھی نقطہ سے مرکز سے فاصلہ کو رداس کہا جاتا ہے۔ اگر ہم دائرے کے فاصلے پر ، وسط سے گزرتے ہوئے ، غور کریں۔ دائرے کے گرد فاصلے کو دائرہ کا طواف کہتے ہیں۔
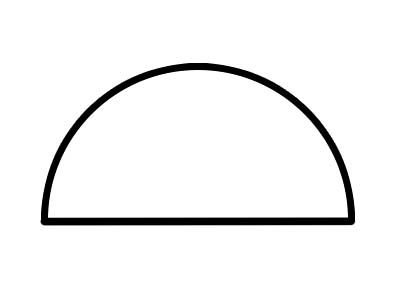
ایک نیم دائرہ ایک نصف دائرے کی حیثیت رکھتا ہے ، جو قطر کی لکیر کے ساتھ پورے دائرے کو کاٹ کر تشکیل دیا جاتا ہے ، جیسا کہ اوپر دکھایا گیا ہے۔ دائرے کا کوئی بھی قطر اسے دو برابر سیمکیرلز میں کاٹتا ہے۔ نیم دائرہ کی مکمل آرک ہمیشہ 180 measures کی پیمائش کرتی ہے۔ اگر کوکی کو دو حصوں میں کاٹ لیا جائے تو ہر ایک آدھ نیم دائرے میں ہوتا ہے۔

انڈاکار میں انڈے کی شکل ، شکل یا خاکہ ہوتا ہے۔ انڈاکار میں سیدھے رخ اور کونے نہیں ہوتے ہیں ، لیکن اس کا 1 چہرہ ہوتا ہے ، جس کو تلاش کرتے وقت اسے فلیٹ شکل کے طور پر دیکھا جاسکتا ہے۔
کثیرالاضلہ ایک طیارے کی شکل ہے جس میں سیدھی لکیریں ہیں۔ مثالوں میں مثلث ، چوکور ، پینٹاگون ، ہیکساگن وغیرہ شامل ہیں۔ ایک باقاعدہ کثیرالاضعی کے تمام اطراف برابر اور تمام زاویے برابر ہیں۔ بصورت دیگر ، یہ ایک فاسد کثیرالاضاع ہے۔
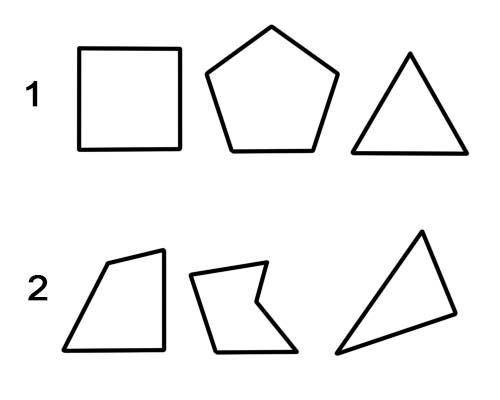
1. باقاعدہ کثیرالاضلاع۔
2. فاسد کثیرالاضلاع۔
حلقے اور شکلیں جن میں منحنی خطوط شامل ہیں کثیرالاضلاع نہیں ہیں - ایک کثیرالعمل ، تعریف کے مطابق ، سیدھے لکیروں سے بنا ہوتا ہے۔

جیومیٹری میں ، ایک مثلث ایک بند ، دو جہتی شکل ہے جس میں تین سیدھی لکیریں ہیں۔ ایک مثلث بھی کثیرالاضلاع ہے۔
ہم کسی جھنڈے ، سڑک کے کنارے سائن بورڈ اور سینڈویچ میں مثلث کی شکل پاسکتے ہیں۔
ایک مثلث کے تین اطراف ، تین عمودی ، اور تین کونے ہیں۔
ایک مثلث کے تین داخلی زاویوں کا مجموعہ ہمیشہ 180 ° ہوتا ہے۔ کسی مثلث کے دونوں اطراف کی لمبائی کا مجموعہ ہمیشہ تیسری طرف کی لمبائی سے زیادہ ہوتا ہے۔
مثلث کو ان کے زاویوں کے مطابق درجہ بندی کرنے کے لئے ، ہم اس کے اندرونی زاویوں میں سے ہر ایک کی پیمائش کرتے ہیں۔ مثلث زاویوں سے درجہ بندی کی جاسکتی ہیں ، جیسے:
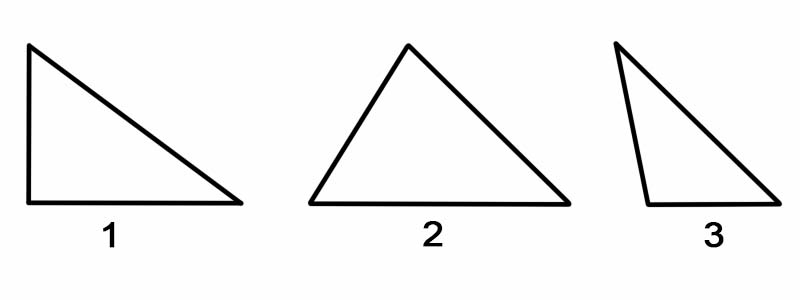
مثلث کو ان کے اطراف کے مطابق درجہ بندی کرنے کے لئے ، ہم اس کے ہر اطراف کی لمبائی کی پیمائش کرتے ہیں۔ مثلث کو ان کے اطراف سے درجہ بندی کیا جاسکتا ہے ، جیسے:
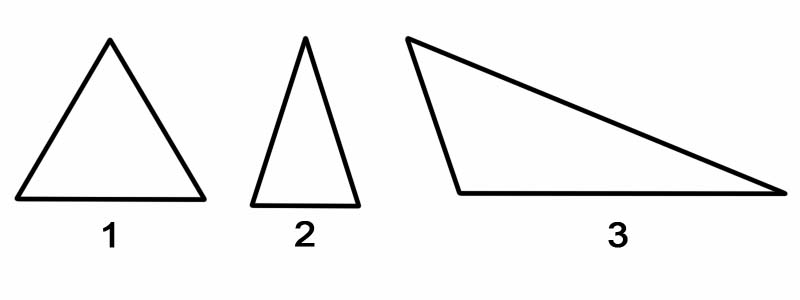
یاد رکھیں: ایک مثلث ہمیشہ اس کی سمت سے قطع نظر ، دو دائیں مثلث میں تقسیم کیا جاسکتا ہے۔
مثلث اطراف کی کم سے کم تعداد کے ساتھ کثیر الاضلاع ہیں۔
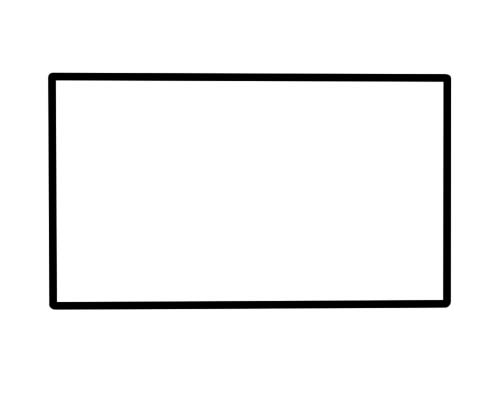
مستطیل ایک ایسی شکل ہے جس کے 4 اطراف ، 4 عمودی ، اور 4 کونے ہیں۔ مخالف فریق لمبائی میں متوازی اور برابر ہیں۔ تمام 4 کونے 90 ڈگری کی پیمائش کرتے ہیں۔
میزیں ، بکس ، کتابیں ، دروازے اور کاغذ مستطیل کی طرح نظر آتے ہیں۔

رومبس ایک شکل ہے جو 4 سیدھی لائنوں سے تشکیل پاتی ہے۔ اس کے 4 اطراف ایک ہی لمبائی کی پیمائش کرتے ہیں لیکن ، مستطیل کے برعکس ، تمام 4 زاویوں میں سے کوئی بھی 90 ڈگری کی پیمائش نہیں کرتا ہے۔ ایک رومبس ہیرے کی طرح لگتا ہے۔ مخالف فریق متوازی اور مخالف زاویہ برابر ہیں۔ ایک رومبس کے دو خامیاں ایک دوسرے کے لئے کھڑے ہیں۔

ایک مربع ایک جہتی شخصیت ہے جس کی لمبائی چاروں اطراف کے برابر ہے اور دونوں مخالف فریق ایک دوسرے کے متوازی ہیں۔ یہ مستطیل اور رومبس کی ایک قسم ہے (ذیل میں بحث کی گئی ہے)۔ مربع کے 4 داخلی زاویے 90º ہیں ، یا دوسرے الفاظ میں ، وہ صحیح زاویہ ہیں۔ جب تمام زاویے ایک ساتھ شامل ہوجاتے ہیں تو وہ 360º تک کا اضافہ کردیتے ہیں۔ ایک مربع کے دو اختیاری لمبائی کے برابر اور جس مقام پر وہ گزرتے ہیں وہ مربع کا مرکز ہے۔
یاد رکھیں: ایک مربع ہمیشہ رومبس ہوتا ہے لیکن رومبس ہمیشہ مربع نہیں ہوتا ہے۔ اگر ایک رومبس کا ہر زاویہ 90o ہے ، تب ہی یہ مربع ہے۔
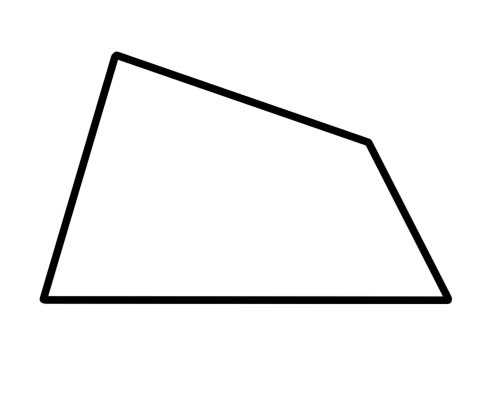
ایک ٹریپیزیم ایک چوکور ہوتا ہے جس میں صرف دو اطراف متوازی ہوتے ہیں۔
یہی ہے. کسی بھی فریق کو یکجا (یا مساوی) ہونے کی ضرورت نہیں ہے اور کسی زاویے کو ایک ساتھ رکھنے کی ضرورت نہیں ہے۔ اخترن کے ساتھ کچھ خاص نہیں ہوتا ہے۔ ایک خاص قسم کا ٹراپیزیم 'آئوسیلز ٹریپیزیم' ہے جس کی لمبائی کے مخالف فریق اور ایک ہی پیمانے کے مخالف زاویے ہیں۔ اخترن بھی برابر لمبائی کے ہیں۔
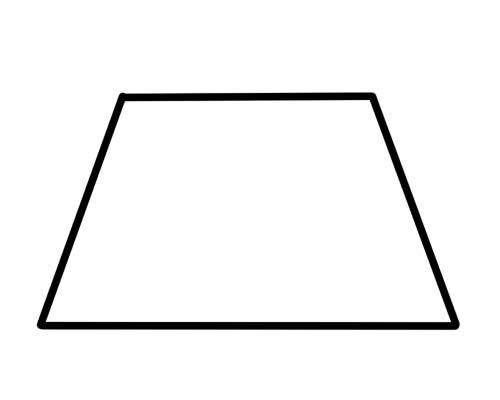
آئسسلز مثلث میں ، اطراف کے ساتھ ملحقہ زاویہ (ایک دوسرے کے زاویہ) ضمنی ہیں۔ اس کا مطلب ہے کہ ان میں 180 ڈگری تک اضافہ ہوتا ہے۔
ٹراپیزیم متوازیگرام نہیں ہے کیونکہ مخالف فریقوں میں سے صرف ایک جوڑا متوازی ہوتا ہے۔
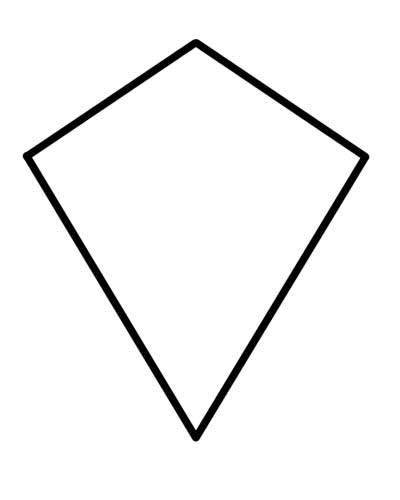
پتنگ چوکور برابر ہے جس کے برابر لگاتار دو جوڑے ہوتے ہیں یا جس میں لگاتار دونوں فریق جوڑے ایک دوسرے کے ساتھ ہوتے ہیں (جدا جدا جوڑ کا مطلب ہے کہ ایک طرف دونوں جوڑے میں استعمال نہیں ہوسکتا)۔
آپ کو یہ جاننے کی ضرورت ہے کہ ہر رومبس ایک پتنگ ہے ، کیونکہ رومبس ایک پتنگ کی تمام خصوصیات کو پورا کرتا ہے۔ متوازی مخالف سمت والا پتنگ یقینی طور پر رومبس بن جاتا ہے۔ اس طرح ہر رومبس ایک پتنگ ہے لیکن اس کے برعکس نہیں۔ پتنگ ایک متوازیگرام نہیں ہے کیونکہ مخالف فریق ایک دوسرے کے متوازی نہیں ہوتے ہیں۔
چوکور - چار طرفہ شخصیت کو چوکور کہا جاتا ہے
متوازیگرام - ایک متوازیگرام ایک فلیٹ شکل ہے جس کے برعکس اطراف متوازی اور لمبائی کے برابر ہیں۔
اس طرح ، مستطیل ، مربع ، رومبس ، ٹریپیزیم اور پتنگ کی شکلیں چوکور ہیں کیونکہ ان کے چار اطراف ہیں۔
تاہم ، صرف مستطیل ، مربع اور رومبس متوازیگرام ہیں۔
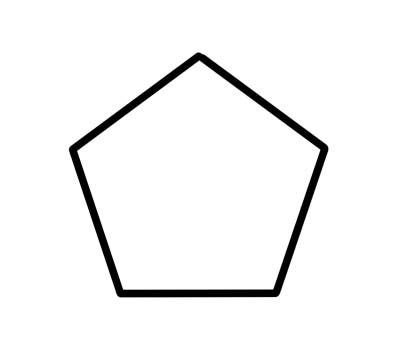
پینٹاگون 5 رخا والا کثیرالاضلاع ہے جس میں پانچ داخلہ زاویہ ہوتے ہیں جو 540 ڈگری میں شامل ہوتے ہیں۔ باقاعدہ پینٹاگون کی لمبائی برابر ہوتی ہے اور ہر داخلی زاویہ 108 ڈگری کا ہوتا ہے۔
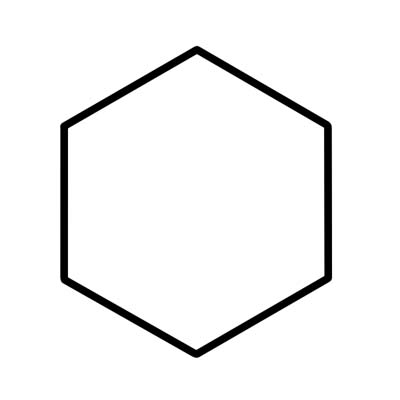
ایک مسدس ایک 6 رخا والا کثیرالاضع ہے جس میں چھ داخلی زاویے ہوتے ہیں جو 720 ڈگری میں شامل کرتے ہیں۔ فاسد مسدس کی لمبائی مختلف ہوتی ہے۔
ایک باقاعدہ مسدس کی لمبائی برابر ہوتی ہے اور ہر داخلی زاویہ 120 ڈگری کا ہوتا ہے۔ ایک باقاعدہ مسدس چھ متناسب مثلث پر مشتمل ہوتا ہے جس میں ہر مرکزی زاویہ 60 ڈگری کے برابر ہوتا ہے۔
[تصویر داخل کریں: مسدس کو چھ مثلث میں تقسیم کیا گیا ہے اور ایک وسطی زاویہ جس کی پیمائش 60 ڈگری ہے]
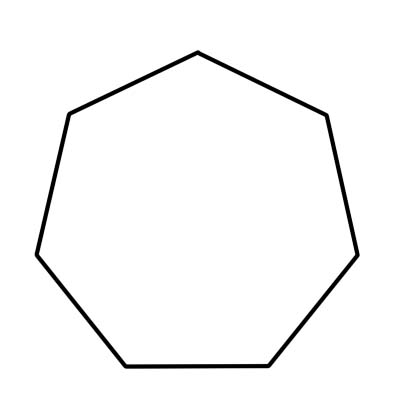
ہیٹاگون ایک سات رخا کثیرالاضلاع ہے۔ سات اطراف کے ساتھ ، ایک ہیٹاگون کے سات عمودی اور کونے ہیں۔ تمام اندرونی زاویوں میں 900 ڈگری کا اضافہ ہوتا ہے۔ ایک باقاعدہ ہیپاٹون کے ہر اندرونی زاویہ کی پیمائش تقریبا 128.57 ڈگری یا تقریبا 129 ڈگری ہے۔
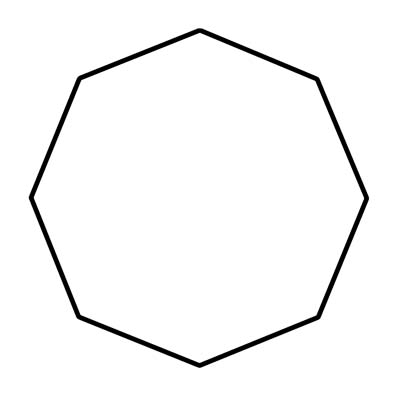
آکٹون ایک ہندسی شکل ہے جس میں آٹھ اطراف اور آٹھ زاویے شامل ہیں۔ آکٹاگون کے سیدھے رخ ہونا ضروری ہیں جو آپس میں ملتے ہیں۔ وہ مڑے ہوئے یا منقطع نہیں ہوسکتے ہیں۔ آپ اکثر اسٹاپ سائن کی شکل میں حقیقی زندگی میں آکٹگنز دیکھیں گے۔ ایک مستقل آکٹون کے آٹھ اندرونی زاویوں میں سے ہر ایک کی پیمائش تقریبا 108 ڈگری ہے۔ محدب آکٹون کے اندر کی طرف اشارہ کرنے کے کوئی زاویے نہیں ہوتے ہیں۔ زیادہ واضح طور پر ، کوئی اندرونی زاویہ 180 more سے زیادہ نہیں ہوسکتا ہے۔ جب کوئی داخلی زاویہ 180 greater سے زیادہ ہوتا ہے تو وہ مقعر ہوتا ہے
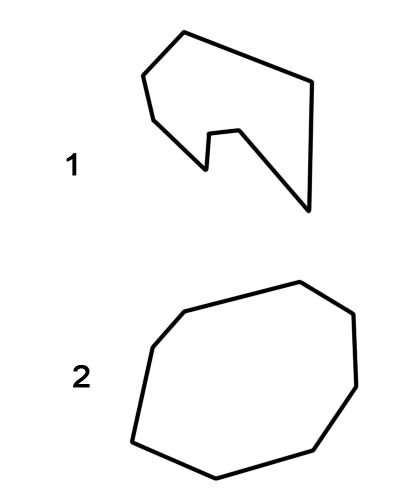
1. کونکیو آکٹون
2. محدب آکٹون
یہ نوٹ کرنا ضروری ہے کہ باقاعدہ آکٹگون کو ہمیشہ محدب آکٹاگن کے طور پر درجہ بند کیا جاتا ہے ، جبکہ فاسد آکٹگن یا تو مقعر یا محدب ہوسکتے ہیں۔
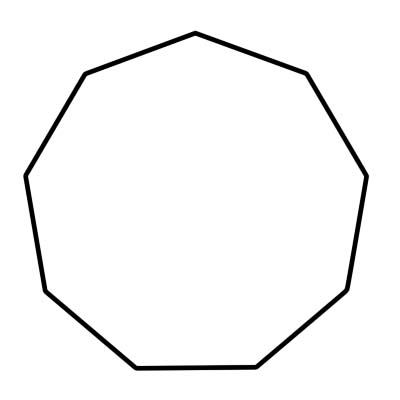
ایک نانگون ایک کثیرالاضع ہے جس میں 9 اطراف اور 9 داخلی زاویے ہیں جو 1260 ڈگری میں شامل ہوتے ہیں۔ ایک باقاعدہ نوناگون ایک ہی لمبائی کے تمام اطراف اور تمام داخلی زاویہ ایک ہی سائز کے ہوتے ہیں۔ باقاعدہ نانگون کے زاویہ کی پیمائش 140 ڈگری ہے۔ ایک مرکزی عضو 40 ڈگری کے برابر ہر مرکزی زاویہ کی پیمائش کے ساتھ 9 مثلث پر مشتمل ہے۔
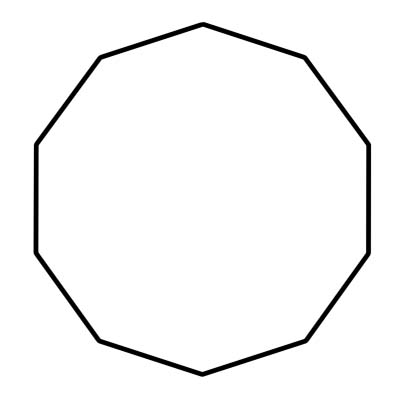
ایک ڈیجون ایک 10 رخا کثیرالاضلہ ہے۔ اس کی دس چوڑیاں بھی ہیں - یہ وہ جگہ ہے جہاں فریق ملتے ہیں - اور زاویہ۔ ایک کٹہرے کے اندرونی زاویوں کا مجموعہ 1440 ڈگری ہے۔ ایک مستقل عشقیہ میں ضمنی اور زاویہ ہوتے ہیں۔ ہر زاویہ 144 ڈگری کی پیمائش کرتی ہے۔ ایک ڈیکون 10 مثلث پر مشتمل ہوتا ہے جس کا مرکزی زاویہ 36 ڈگری کے برابر ہوتا ہے۔
وہ اشکال جو تین جہتوں میں ماپا جاسکتے ہیں وہ تین جہتی شکلیں یا 3D شکلیں کہلاتی ہیں۔ 3D شکلیں بھی ٹھوس شکلیں کہلاتی ہیں۔ 3D شکلوں کی تین پیمائشیں ہیں - لمبائی ، چوڑائی اور اونچائی (یا گہرائی یا موٹائی)۔
3D شکلیں 2D شکلوں سے مختلف ہوتی ہیں کیونکہ ان کی موٹائی ہوتی ہے۔ ہماری روزمرہ کی زندگی کی 3D شکلوں کی کچھ مثالیں یہ ہیں:
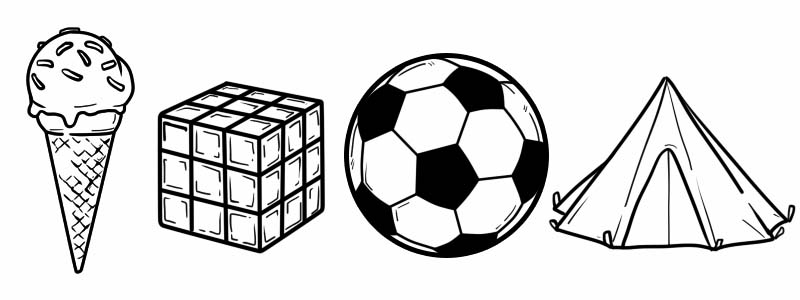
جہتی شکلوں میں چوڑیاں ، چہرے اور کنارے ہوتے ہیں۔
پرزم ایک قسم کا سہ رخی (3D) شکل ہے جس میں فلیٹ اطراف ہیں۔ اس کے دو سرے ہیں جو ایک ہی شکل اور سائز (اور ایک 2D شکل کی طرح نظر آتے ہیں) ہیں۔ اس کا اختتام سے آخر تک شکل کے ساتھ ساتھ ایک ہی کراس سیکشن ہے۔ اس کا مطلب ہے کہ اگر آپ اس کو کاٹتے ہیں تو آپ کو اسی طرح 2D شکل نظر آتی ہے جس کی دونوں طرف ہے۔
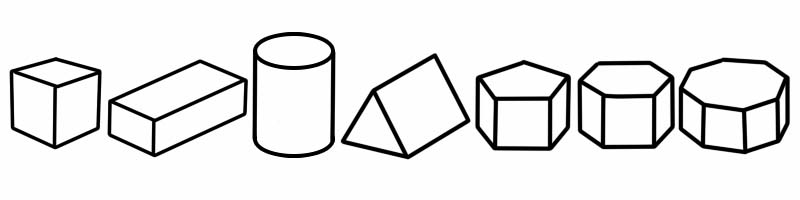
3D شکل | کناروں کی تعداد | چہروں کی تعداد | افقیوں کی تعداد |
مکعب | 12 | 6 | 8 |
کیوبائڈ | 12 | 6 | 8 |
سلنڈر | 2 | 3 | 0 |
تکونی منشور | 9 | 5 (2 مثلث ، 3 مستطیل) | 6 |
پینٹاگونل پرزم | 15 | 7 | 10 |
مسدس پرزم | 18 | 8 | 12 |
آکٹاگونل پرزم | 24 | 10 | 16 |
ایک اہرام ایک سہ جہتی (3D) شکل بھی ہے۔ اس میں کثیرالاضافہ کی بنیاد اور فلیٹ (سہ رخی) اطراف ہوتے ہیں جو مشترکہ نقطہ پر شامل ہوتے ہیں (جسے چوٹی کہا جاتا ہے)۔ جب لفظ 'اہرامڈ' کا تذکرہ کیا جاتا ہے تو ، سب سے پہلے جو بات ہمارے ذہنوں میں آتی ہے وہ مصر کے مشہور اہرامے ہیں۔ مصری اہرام مربع پر مبنی اہرام ہیں ، لیکن اہرام کی متعدد دوسری اقسام ہیں ، جن میں سے ہر ایک کا الگ الگ کثیرالاضلہ ہوتا ہے۔
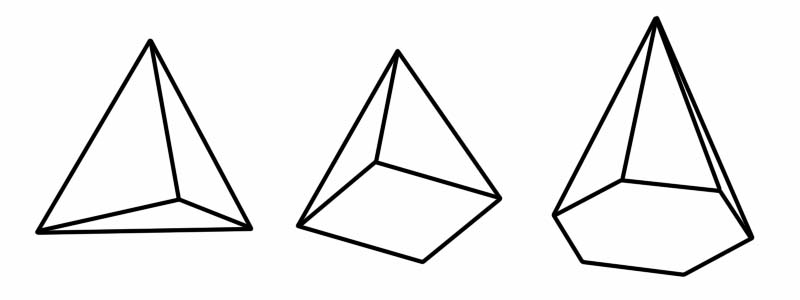
شکل | کناروں کی تعداد | چہروں کی تعداد | افقیوں کی تعداد |
ٹیٹراہیدران | 6 | 4 | 4 |
مربع اہرام | 8 | 5 | 5 |
ہیکساگونل اہرام | 12 | 7 | 7 |
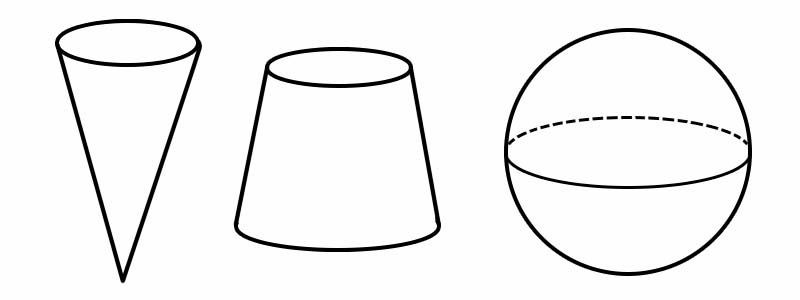
شکل | کناروں کی تعداد | چہروں کی تعداد | افقیوں کی تعداد |
مخروط | 1 | 2 | 1 |
فروسٹم | 2 | 3 | 0 |
کرہ | 0 | 1 | 0 |