يُشار إلى المضلع على أنه شكل مستوي يتم وصفه بعدد محدود من مقاطع الخط المستقيمة المتصلة لتشكيل سلسلة مضلعة مغلقة أو دائرة مضلعة. يمكن أن تسمى الدائرة المحيطة أو منطقة المستوى الصلب أو مزيج الاثنين مضلع.
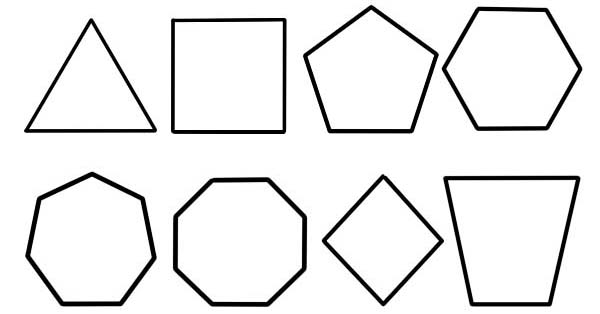
يشار إلى عناصر الدائرة المضلعة إلى حوافها أو يشار إليها أحيانًا بالجوانب ، ونقطة التقاء لحافتين هي ما يشار إليه باسم زاوية أو قمم مضلع. ويشار إليها في شكلها المفرد بالرأس. يُشار أحيانًا إلى الجزء الداخلي من المضلع الصلب إلى جسمه. n-gon هو مصطلح يستخدم لمضلع له عدد من الأضلاع. على سبيل المثال: المستطيل هو 4-gon.
يمكن القول بأن المضلع الذي لا يتقاطع مع نفسه هو مضلع بسيط. يهتم علماء الرياضيات في الغالب بالسلاسل المضلعة من المضلعات البسيطة التي غالبًا ما تحدد أو تصف المضلع وفقًا لذلك. يمكن تكوين المضلعات النجمية وكذلك المضلعات ذاتية التقاطع حيث يسمح بحدود مضلعة بعبور نفسها.
المضلع هو مثال لبعدين للمضلع الأكثر شيوعًا في أي رقم بعد. يوجد العديد من التعميمات المضلعة التي تم تحديدها لأغراض مختلفة.
تصنيف المضلعات.
يمكن تصنيف المضلعات بعدة طرق مختلفة. تتضمن قواعد تصنيفها ما يلي:
- عدد الجوانب. هذه هي القاعدة الأساسية والأكثر شيوعًا لتصنيف المضلعات.
- التحدب وعدم التحدب. تحت هذا ، يمكن تجميعهم فرعيًا في:
- محدب. أي خط يتم رسمه من خلال المضلع ويفي بالحدود مرتين. ونتيجة لذلك ، فإن جميع الزوايا في الداخل أقل من 180 0 .
- غير محدب. خط يمكن العثور عليه ليلبي الحد أكثر من مرتين. وبالمثل ، يوجد مقطع خط بين نقطتين حدويتين تمر خارج المضلع.
- مقعر. هذه بسيطة وغير محدبة. زاوية داخلية واحدة على الأقل أكبر من 180 0 .
- بسيط. حدود المضلع لا تعبر نفسها.
- على شكل نجمة. يمكن رؤية الداخل بأكمله من نقطة واحدة على الأقل.
- مضلع النجم. مضلع يتقاطع مع نفسه بطريقة منتظمة.
- المساواة والتماثل.
- متساوي الزوايا. جميع الزوايا متساوية. (زوايا الزاوية).
- دوري. ترتكز جميع الزوايا على دائرة واحدة تسمى الدائرة.
- تماسي. هذا هو المكان الذي تكون فيه جميع الجوانب مماسة لدائرة منقوشة.
- متساوي الاضلاع. هذا هو المكان الذي يكون لجميع الأعمار نفس الطول.
- Vertex متعد أو متساوي الأضلاع. هذا هو المكان الذي ترتاح فيه جميع الزوايا في مدار مماثل.
- منتظم. ينطبق هذا عندما يكون المضلع متساوي السمية ومتساوي الأضلاع. وبالمثل ، فهي متساوية الأضلاع ودورية أو متساوية الأضلاع ومتساوية. المضلع النجمي هو الاسم الذي يطلق على المضلع غير المحدب المنتظم.
- متنوع. يشملوا:
الملائكة.
النوعان الأكثر شيوعًا من الزوايا هما الزوايا الداخلية والخارجية.
- الزاوية الداخلية. يتم إعطاء مجموع الزوايا الداخلية لـ n-gon البسيط على شكل راديان (n - 2) π. يمكن الحصول عليها أيضًا بـ (n - 2) x 180 درجة.
- خارج، الزاوية. هذه زوايا تكميلية للزوايا في الداخل.
