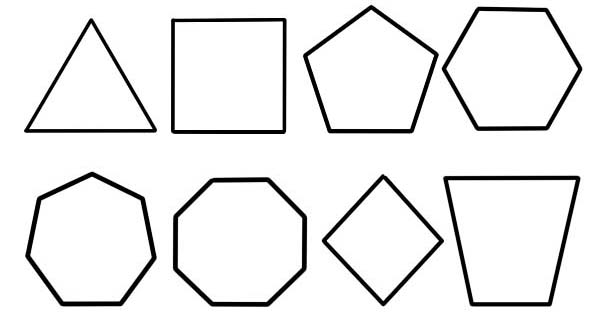
বহুভুজকে সমতল চিত্র বলা হয় যার বর্ণনা সীমিত সংখ্যক রেখাংশ দ্বারা করা হয় যা সোজা যা বন্ধ হয়ে যাওয়া বহুভুজ শৃঙ্খল বা বহুভুজ সার্কিট গঠনের সাথে সংযুক্ত থাকে। বাউন্ডিং সার্কিট, কঠিন সমতল অঞ্চল বা দুটির সংমিশ্রণকে বহুভুজ বলা যেতে পারে।
একটি বহুভুজ সার্কিটের উপাদানগুলিকে তার প্রান্ত বা কখনও কখনও পক্ষ হিসাবে উল্লেখ করা হয় এবং দুটি প্রান্তের মিলন বিন্দুকে বহুভুজের কোণ বা শীর্ষবিন্দু বলা হয়। তার একবচনে এটি একটি শীর্ষবিন্দু হিসাবে উল্লেখ করা হয়। একটি কঠিন বহুভুজের অভ্যন্তর কখনও কখনও তার দেহকে উল্লেখ করা হয়। একটি n-gon হল একটি শব্দ যা বহুভুজের সাথে ব্যবহৃত হয় যার n সংখ্যা রয়েছে। উদাহরণস্বরূপ: একটি আয়তক্ষেত্র একটি 4-গন।
যে বহুভুজটি নিজেকে ছেদ করে না, তাকে সাধারণ বহুভুজ বলা যেতে পারে। গণিতবিদরা বেশিরভাগ বহুভুজের বহুভুজ শৃঙ্খল নিয়ে উদ্বিগ্ন যা প্রায়শই সেই অনুসারে বহুভুজকে সংজ্ঞায়িত বা বর্ণনা করে। স্টার বহুভুজের পাশাপাশি স্ব-ছেদকারী বহুভুজ গঠিত হতে পারে যেখানে একটি বহুভুজ সীমানা নিজেই অতিক্রম করার অনুমতি দেওয়া হয়।
বহুভুজ হল যেকোনো মাত্রা সংখ্যায় অধিক সাধারণ পলিটোপের 2 মাত্রিক একটি উদাহরণ। আরও বহুভুজের সাধারণীকরণ বিদ্যমান যা বিভিন্ন উদ্দেশ্যে সংজ্ঞায়িত করা হয়।
পলিগনের শ্রেণীবিন্যাস।
বহুভুজকে বিভিন্ন উপায়ে শ্রেণিবদ্ধ করা যায়। শ্রেণিবিন্যাসের ভিত্তির মধ্যে রয়েছে:
- পক্ষের সংখ্যা। এটি বহুভুজের শ্রেণিবিন্যাসের প্রাথমিক এবং সবচেয়ে সাধারণ ভিত্তি।
- উত্তলতা এবং অ-উত্তলতা। এর অধীনে, তাদের এই উপ-গ্রুপে ভাগ করা যেতে পারে:
- উত্তল। যেকোনো রেখা যা বহুভুজের মাধ্যমে টানা হয় এবং সীমানা দুইবার পূরণ করে। এর ফলস্বরূপ, এর অভ্যন্তরের সমস্ত কোণ 180 0 এর কম।
- অ-উত্তল। একটি রেখা যা সীমানার সাথে দুইবারের বেশি দেখা যেতে পারে। সমানভাবে, দুটি সীমানা পয়েন্টের মধ্যে একটি রেখাংশ বিদ্যমান যা বহুভুজের বাইরে চলে যায়।
- অবতল। এগুলি সহজ এবং উত্তল নয়। অন্তত একটি অভ্যন্তরীণ কোণ 180 0 এর চেয়ে বড়।
- সরল। বহুভুজের সীমানা নিজেই অতিক্রম করে না।
- নক্ষত্র আকৃতির। কমপক্ষে একটি বিন্দু থেকে পুরো অভ্যন্তরটি দেখা যায়।
- নক্ষত্র বহুভুজ। একটি বহুভুজ যা নিয়মিতভাবে নিজেকে ছেদ করে।
- সমতা এবং প্রতিসাম্যতা।
- ইকিয়াঙ্গুলার। সব কোণ সমান। (কোণ কোণ)।
- চক্রাকার। সমস্ত কোণগুলি একটি একক বৃত্তে বিশ্রাম নেয় যাকে সার্কুলার বলা হয়।
- স্পর্শকাতর। এখানেই সব দিক খোদাই করা একটি বৃত্তের স্পর্শক।
- সমবাহু। এখানেই সব বয়সের দৈর্ঘ্য সমান।
- ভারটেক্স ট্রানজিটিভ বা আইসোগোনাল। এই যেখানে সব কোণ একটি অনুরূপ প্রতিসাম্য কক্ষপথ মধ্যে বিশ্রাম।
- নিয়মিত। এটি প্রযোজ্য যেখানে বহুভুজ isotoxal এবং isogonal উভয়। সমানভাবে, এটি সমবাহু এবং চক্রীয় উভয়ই বা সমতুল্য এবং সমবাহু উভয়ই। স্টার বহুভুজ হল একটি অ-উত্তল বহুভুজকে দেওয়া নাম যা নিয়মিত।
- বিবিধ। তারা সংযুক্ত:
কোণ।
দুটি সবচেয়ে সাধারণ ধরনের কোণ হল অভ্যন্তর এবং বহিস্থ কোণ।
- অভ্যন্তরীণ কোণ। একটি সাধারণ n-gon এর অভ্যন্তরীণ কোণের সমষ্টি (n-2) π রেডিয়ান হিসাবে দেওয়া হয়। এটি (n - 2) x 180 ডিগ্রী দ্বারাও পাওয়া যায়।
- বাহ্যিক কোণ। এগুলি অভ্যন্তরের কোণের পরিপূরক কোণ।
