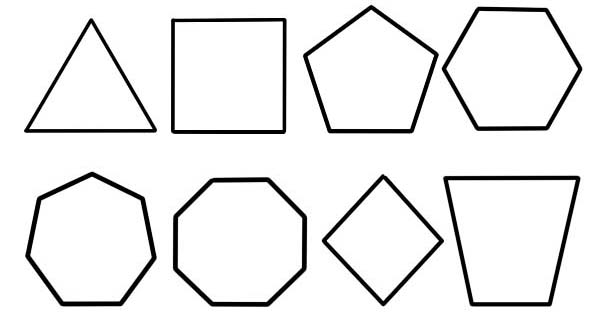
Ein Polygon wird als ebene Figur bezeichnet, deren Beschreibung durch eine endliche Anzahl von geraden Liniensegmenten erfolgt, die zu einer geschlossenen Polygonkette oder einem polygonalen Kreis verbunden sind. Die Begrenzungsschaltung, der Bereich der durchgezogenen Ebene oder die Kombination der beiden kann als Polygon bezeichnet werden.
Die Elemente einer polygonalen Schaltung werden auf ihre Kanten oder manchmal als Seiten bezeichnet, und der Treffpunkt zweier Kanten wird als Ecke oder Eckpunkte eines Polygons bezeichnet. In seiner Singularform wird es als Scheitelpunkt bezeichnet. Das Innere eines festen Polygons wird manchmal auf seinen Körper bezogen. Ein n-Gon ist ein Begriff, der für ein Polygon mit n Seiten verwendet wird. Zum Beispiel: Ein Rechteck ist ein 4-Gon.
Ein Polygon, das sich nicht schneidet, kann als einfaches Polygon bezeichnet werden. Mathematiker beschäftigen sich hauptsächlich mit den Polygonketten aus einfachen Polygonen, die häufig ein Polygon entsprechend definieren oder beschreiben. Sternpolygone sowie sich selbst schneidende Polygone können dort gebildet werden, wo sich eine polygonale Grenze kreuzen darf.
Ein Polygon ist ein Beispiel für eine zweidimensionale des allgemeineren Polytops in einer beliebigen Dimensionsnummer. Es gibt viel mehr Verallgemeinerungen von Polygonen, die für verschiedene Zwecke definiert sind.
KLASSIFIZIERUNG VON POLYGONEN.
Polygone können auf viele verschiedene Arten klassifiziert werden. Ihre Klassifizierungsgrundlagen umfassen:
- Anzahl der Seiten. Dies ist die primäre und häufigste Grundlage für die Klassifizierung von Polygonen.
- Konvexität und Nichtkonvexität. Darunter können sie unterteilt werden in:
- Konvex. Jede Linie, die durch das Polygon gezogen wird und die Grenze zweimal trifft. Infolgedessen sind alle Winkel in seinem Inneren kleiner als 180 ° .
- Nicht konvex. Eine Linie, die mehr als zweimal die Grenze trifft. Entsprechend existiert ein Liniensegment zwischen zwei Grenzpunkten, das außerhalb des Polygons verläuft.
- Konkav. Diese sind einfach und nicht konvex. Zumindest ein Innenwinkel größer ist als 180 0.
- Einfach. Die Grenze des Polygons überschreitet sich nicht.
- Sternförmig. Der gesamte Innenraum ist mindestens von einem Punkt aus sichtbar.
- Sternpolygon. Ein Polygon, das sich regelmäßig schneidet.
- Gleichheit und Symmetrie.
- Gleichwinklig. Alle Winkel sind gleich. (Eckwinkel).
- Zyklisch. Alle Ecken ruhen auf einem einzigen Kreis, der als Kreis bezeichnet wird.
- Tangential. Hier sind alle Seiten eine Tangente an einen eingeschriebenen Kreis.
- Gleichseitig. Hier haben alle Altersgruppen die gleiche Länge.
- Scheitelpunkt transitiv oder isogonal. Hier liegen alle Ecken in einer ähnlichen Symmetriebahn.
- Regulär. Dies gilt, wenn das Polygon sowohl isotoxal als auch isogonal ist. Gleichermaßen ist es sowohl gleichseitig als auch zyklisch oder sowohl gleichwinklig als auch gleichseitig. Sternpolygon ist der Name eines nicht konvexen Polygons, das regelmäßig ist.
- Verschiedenes. Sie beinhalten:
WINKEL.
Die beiden häufigsten Arten von Winkeln sind die Innen- und Außenwinkel.
- Innenwinkel. Die Summe der Innenwinkel für ein einfaches n-Gon wird als (n - 2) π Radiant angegeben. Es kann auch um (n - 2) x 180 Grad erreicht werden.
- Außenwinkel. Dies sind zusätzliche Winkel zu den Winkeln im Innenraum.
