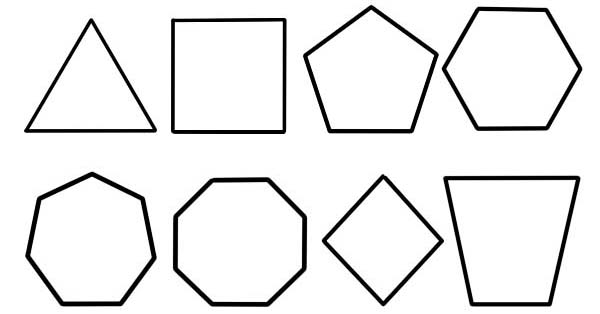
چند ضلعی به شکل صفحه ای گفته می شود که توصیف آن توسط تعداد محدودی از پاره های خط مستقیم انجام می شود که به هم متصل می شوند تا یک زنجیره چند ضلعی بسته یا یک مدار چند ضلعی را تشکیل دهند. مدار مرزی، ناحیه صفحه جامد یا ترکیب این دو را می توان چندضلعی نامید.
عناصر یک مدار چند ضلعی به لبه های آن یا گاهی اوقات به عنوان اضلاع نامیده می شوند و نقطه تلاقی دو یال همان چیزی است که به عنوان گوشه یا رئوس چند ضلعی از آن یاد می شود. در شکل مفرد آن به عنوان راس شناخته می شود. درون یک چند ضلعی جامد گاهی اوقات به بدنه آن اشاره می شود. n-gon اصطلاحی است که برای چند ضلعی استفاده می شود که n تعداد ضلع دارد. به عنوان مثال: یک مستطیل 4 ضلعی است.
چند ضلعی که خود را قطع نمی کند، می توان گفت که چند ضلعی ساده است. ریاضیدانان بیشتر به زنجیره های چند ضلعی از چند ضلعی های ساده می پردازند که اغلب یک چند ضلعی را بر این اساس تعریف یا توصیف می کنند. چند ضلعی های ستاره ای و همچنین چند ضلعی های خود متقاطع ممکن است در جایی تشکیل شوند که یک مرز چند ضلعی اجازه عبور از خود را داشته باشد.
چند ضلعی نمونه ای از دو بعدی پلی توپ رایج تر در هر عدد بعدی است. بسیاری از تعمیم های چندضلعی وجود دارد که برای اهداف مختلف تعریف شده اند.
طبقه بندی چند ضلعی ها.
چند ضلعی ها را می توان به روش های مختلفی طبقه بندی کرد. مبانی طبقه بندی آنها عبارتند از:
- تعداد اضلاع این اصلی ترین و رایج ترین پایه طبقه بندی چند ضلعی ها است.
- تحدب و عدم تحدب. تحت این، آنها را می توان به زیر گروه بندی کرد:
- محدب. هر خطی که از چند ضلعی کشیده شود و دو بار به مرز برسد. در نتیجه تمام زوایای داخل آن کمتر از 180 0 است.
- غیر محدب. خطی که ممکن است بیش از دو بار به مرز برسد. به طور معادل، یک پاره خط بین دو نقطه مرزی وجود دارد که از خارج از چند ضلعی می گذرد.
- مقعر. اینها ساده و غیر محدب هستند. حداقل یک زاویه داخلی بزرگتر از 180 0 باشد.
- ساده. مرز چند ضلعی از خود عبور نمی کند.
- ستاره ای شکل. کل فضای داخلی را می توان حداقل از یک نقطه دید.
- چند ضلعی ستاره ای. چند ضلعی که خود را به صورت منظم قطع می کند.
- برابری و تقارن.
- متساوی الاضلاع. همه زوایا برابرند. (زوایای گوشه).
- چرخه ای. تمام گوشه ها بر روی یک دایره قرار می گیرند که به آن دایره اطلاق می شود.
- مماس. این جایی است که تمام اضلاع مماس بر دایره ای هستند که حکاکی شده است.
- متساوی الاضلاع. این جایی است که تمام سنین طول یکسانی دارند.
- رأس متعدی یا ایزوگونال. اینجا جایی است که تمام گوشه ها در یک مدار تقارن مشابه قرار می گیرند.
- منظم. این در جایی اعمال می شود که چند ضلعی هم ایزوتوکسال و هم ایزوگونال باشد. به طور معادل، هم متساوی الاضلاع است و هم حلقوی یا هم متساوی الاضلاع و هم متساوی الاضلاع. چند ضلعی ستاره ای نامی است که به چند ضلعی غیر محدب که منظم است داده می شود.
- متفرقه آنها عبارتند از:
زاویه.
دو نوع از رایج ترین زاویه ها، زوایای داخلی و خارجی هستند.
- زاویه داخلی. مجموع زوایای داخلی برای یک n-گون ساده به صورت (n – 2) π رادیان داده می شود. همچنین می توان آن را با (n – 2) x 180 درجه بدست آورد.
- زاویه بیرونی اینها زوایای تکمیلی برای زوایای داخلی هستند.
