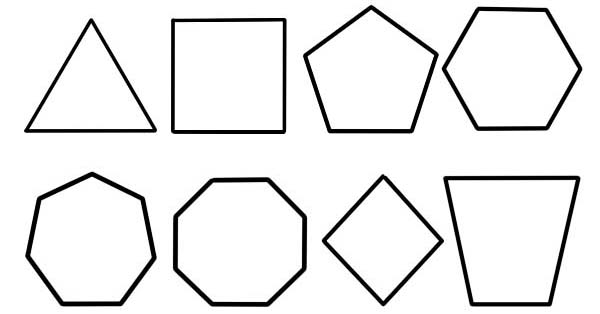
Un polygone est appelé une figure plane dont la description est faite par un nombre fini de segments de droite qui sont connectés pour former une chaîne polygonale fermée ou un circuit polygonal. Le circuit englobant, la région du plan solide ou la combinaison des deux peuvent être appelés un polygone.
Les éléments d'un circuit polygonal sont appelés ses arêtes ou parfois appelés côtés, et le point de rencontre de deux arêtes est ce que l'on appelle le coin ou les sommets d'un polygone. Dans sa forme singulière, il est appelé un sommet. L'intérieur d'un polygone solide est parfois appelé son corps. Un n-gon est un terme qui est utilisé pour un polygone qui a n nombre de côtés. Par exemple: un rectangle est un 4-gon.
Un polygone qui ne se coupe pas peut être considéré comme un simple polygone. Les mathématiciens s'intéressent principalement aux chaînes polygonales à partir de polygones simples qui définissent ou décrivent souvent un polygone en conséquence. Des polygones en étoile ainsi que des polygones auto-sécants peuvent être formés là où une frontière polygonale est autorisée à se croiser.
Un polygone est un exemple de 2 dimensions du polytope le plus courant dans n'importe quel nombre de dimension. Il existe de nombreuses généralisations de polygones qui sont définies à des fins différentes.
CLASSIFICATION DES POLYGONS.
Les polygones peuvent être classés de différentes manières. Leurs bases de classification comprennent:
- Nombre de côtés. Il s'agit de la base principale et la plus courante de classification des polygones.
- Convexité et non-convexité. En vertu de cela, ils peuvent être sous-regroupés en:
- Convexe. Toute ligne tracée à travers le polygone et qui rencontre la limite deux fois. En conséquence, tous les angles de son intérieur sont inférieurs à 180 0 .
- Non convexe. Une ligne qui peut rencontrer la limite plus de deux fois. De manière équivalente, un segment de ligne existe entre deux points de frontière qui passe à l'extérieur du polygone.
- Concave. Ceux-ci sont simples et non convexes. Au moins un angle intérieur est supérieur à 180 0 .
- Facile. La limite du polygone ne se croise pas.
- En forme d'étoile. L'intérieur entier peut être vu d'un point au moins.
- Polygone d'étoile. Un polygone qui se coupe de manière régulière.
- Égalité et symétrie.
- Équiangle. Tous les angles sont égaux. (angles de coin).
- Cyclique. Tous les coins reposent sur un seul cercle que l'on appelle le cercle circulaire.
- Tangentiel. C'est là que tous les côtés sont tangents à un cercle inscrit.
- Équilatéral. C'est là que tous les âges ont la même longueur.
- Vertex transitif ou isogonal. C'est là que tous les coins reposent sur une orbite de symétrie similaire.
- Régulier. Ceci s'applique lorsque le polygone est à la fois isotoxal et isogonal. De manière équivalente, il est à la fois équilatéral et cyclique ou à la fois équiangulaire et équilatéral. Le polygone en étoile est le nom donné à un polygone non convexe régulier.
- Divers. Ils comprennent:
ANGLES.
Les deux types d'angles les plus courants sont les angles intérieurs et extérieurs.
- Angle intérieur. La somme des angles intérieurs pour un simple n-gon est donnée par (n - 2) π radians. Il peut également être obtenu par (n - 2) x 180 degrés.
- Angle extérieur. Ce sont des angles supplémentaires aux angles à l'intérieur.
