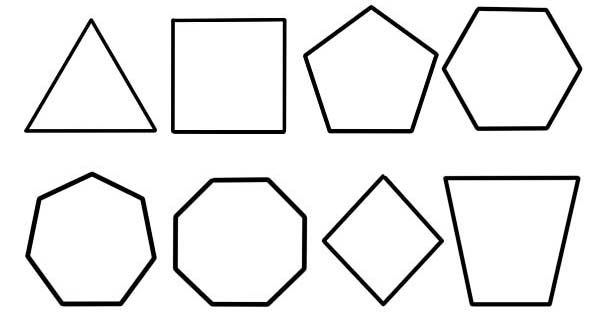
एक बहुभुज को एक विमान आकृति के रूप में संदर्भित किया जाता है जिसका विवरण लाइन खंडों की एक परिमित संख्या द्वारा किया जाता है जो सीधे हैं जो एक बहुभुज श्रृंखला बनाने के लिए जुड़े हुए हैं जो बंद है या एक बहुभुज सर्किट है। बाउंडिंग सर्किट, ठोस विमान क्षेत्र या दोनों के संयोजन को बहुभुज कहा जा सकता है।
एक बहुभुज सर्किट के तत्वों को इसके किनारों या कभी-कभी पक्षों के रूप में संदर्भित किया जाता है, और दो किनारों के मिलन बिंदु को बहुभुज के कोने या कोने के रूप में संदर्भित किया जाता है। अपने विलक्षण रूप में इसे एक शीर्ष के रूप में जाना जाता है। एक ठोस बहुभुज का आंतरिक भाग कभी-कभी इसके शरीर को संदर्भित करता है। एन-गॉन एक शब्द है जिसका उपयोग बहुभुज के लिए किया जाता है जिसमें पक्षों की संख्या n होती है। उदाहरण के लिए: एक आयत 4-गॉन है।
एक बहुभुज जो खुद को नहीं काटता है उसे एक साधारण बहुभुज कहा जा सकता है। गणितज्ञ ज्यादातर बहुभुज से बहुभुज श्रृंखलाओं से संबंधित होते हैं जो अक्सर बहुभुज को परिभाषित या उसके अनुसार वर्णन करते हैं। स्टार बहुभुज के साथ-साथ आत्म-अंतःक्षेपी बहुभुज बन सकते हैं जहां एक बहुभुज सीमा को स्वयं पार करने की अनुमति है।
बहुभुज किसी भी आयाम संख्या में अधिक सामान्य पॉलीटोप के 2 आयामी का एक उदाहरण है। कई और बहुभुज के सामान्यीकरण मौजूद हैं जो विभिन्न उद्देश्यों के लिए परिभाषित किए गए हैं।
पुलिसकर्मियों का वर्गीकरण।
बहुभुज को कई अलग-अलग तरीकों से वर्गीकृत किया जा सकता है। वर्गीकरण के उनके आधारों में शामिल हैं:
- पक्षों की संख्या। यह बहुभुजों के वर्गीकरण का प्राथमिक और सबसे आम आधार है।
- उत्तलता और गैर-उत्तलता। इसके तहत, उन्हें उप-समूहित किया जा सकता है:
- उत्तल। बहुभुज के माध्यम से खींची जाने वाली कोई भी रेखा और सीमा से दो बार मिलती है। इसके परिणामस्वरूप, इसके इंटीरियर के सभी कोण 180 0 से कम हैं।
- गैर-उत्तल। एक रेखा जो दो से अधिक बार सीमा को पूरा करने के लिए मिल सकती है। समान रूप से, एक रेखा खंड दो सीमा बिंदुओं के बीच मौजूद होता है जो बहुभुज के बाहर से गुजरता है।
- अवतल। ये सरल और गैर-उत्तल हैं। कम से कम एक आंतरिक कोण 180 0 से अधिक है।
- सरल। बहुभुज की सीमा खुद को पार नहीं करती है।
- स्टार के आकार का। पूरे इंटीरियर को एक बिंदु से कम से कम देखा जा सकता है।
- तारा बहुभुज। एक बहुभुज जो अपने आप को एक नियमित रूप से प्रतिच्छेदन करता है।
- समानता और समरूपता।
- समानकोणिक। सभी कोण समान हैं। (कोन कोण)।
- चक्रीय। सभी कोनों को एक सर्कल पर आराम दिया जाता है जिसे खतना के रूप में संदर्भित किया जाता है।
- स्पर्शरेखा। यह वह जगह है जहां सभी पक्ष एक सर्कल के लिए एक स्पर्शरेखा है जो अंकित है।
- समभुज। यह वह जगह है जहाँ सभी उम्र एक समान है।
- वर्टेक्स ट्रांसेटिव या आइसोगोनल। यह वह जगह है जहां सभी कोनों को एक समान समरूपता कक्षा के भीतर आराम मिलता है।
- नियमित रूप से। यह लागू होता है जहां बहुभुज आइसोटॉक्सल और आइसोगोनल दोनों होता है। समान रूप से, यह समबाहु और चक्रीय या दोनों समभुज और समबाहु है। स्टार बहुभुज एक गैर-उत्तल बहुभुज का नाम है जो नियमित है।
- विविध। उनमे शामिल है:
कोण।
दो सबसे सामान्य प्रकार के कोण आंतरिक और बाहरी कोण हैं।
- आंतरिक कोण। साधारण एन-गॉन के लिए आंतरिक कोण का योग (n - 2) π रेडियन के रूप में दिया जाता है। यह (n - 2) x 180 डिग्री से भी प्राप्त किया जा सकता है।
- बाहरी कोण। ये इंटीरियर में कोणों के पूरक कोण हैं।
