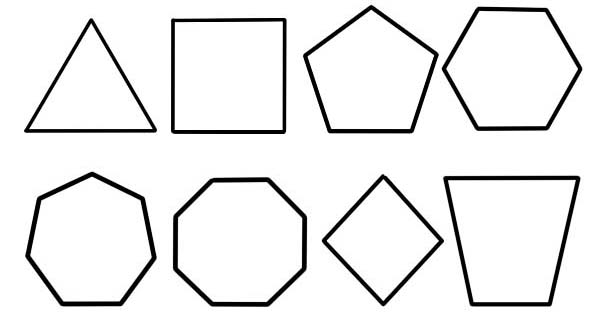
Poligon se naziva plosnati lik čiji se opis vrši konačnim brojem ravnih segmenata koji su povezani da tvore poligonalni lanac koji je zatvoren ili poligonalni krug. Ograničujući krug, područje čvrste ravnine ili njihova kombinacija može se nazvati poligonom.
Elementi poligonalnog kruga nazivaju se njegovim rubovima ili se ponekad nazivaju stranicama, a točka susreta dvaju bridova je ono što se naziva kut ili vrhovi poligona. U svom obliku jednine naziva se vrhom. Unutrašnjost punog poligona ponekad se naziva njegovo tijelo. N-kut je izraz koji se koristi za poligon koji ima n broj strana. Na primjer: pravokutnik je 4-kut.
Poligon koji se ne siječe može se reći da je jednostavan mnogokut. Matematičari se uglavnom bave poligonalnim lancima od jednostavnih poligona koji često definiraju ili u skladu s tim opisuju poligon. Zvjezdasti poligoni kao i poligoni koji se sami sijeku mogu se formirati tamo gdje se poligonalna granica može prijeći.
Poligon je primjer dvodimenzionalnog češćeg politopa u bilo kojem dimenzijskom broju. Postoji mnogo više generalizacija poligona koje su definirane za različite svrhe.
KLASIFIKACIJA MNOGOKUTA.
Poligoni se mogu klasificirati na mnogo različitih načina. Njihove osnove klasifikacije uključuju:
- Broj strana. Ovo je primarna i najčešća baza klasifikacije poligona.
- Konveksnost i nekonveksnost. U skladu s tim, mogu se podijeliti u:
- Konveksan. Svaka linija koja je povučena kroz poligon i dvaput susreće granicu. Zbog toga su svi kutovi u njegovoj unutrašnjosti manji od 180 0 .
- Nekonveksan. Linija za koju se može naći da graniči više od dva puta. Ekvivalentno, segment linije postoji između dvije granične točke koji prolazi izvan poligona.
- Konkavna. One su jednostavne i nekonveksne. Najmanje jedan unutarnji kut veći je od 180 0 .
- Jednostavan. Granica poligona ne prelazi samu sebe.
- U obliku zvijezde. Cijeli interijer može se vidjeti barem s jedne točke.
- Zvjezdani poligon. Poligon koji se siječe na pravilan način.
- Jednakost i simetrija.
- Jednakokutan. Svi kutovi su jednaki. (kutni kutovi).
- Ciklička. Svi uglovi počivaju na jednoj kružnici koja se naziva opisana kružnica.
- Tangencijalni. Ovo je mjesto gdje su sve strane tangente na kružnicu koja je upisana.
- Jednakostraničan. Ovdje svi uzrasti imaju istu duljinu.
- Vertex tranzitivan ili izogonan. Ovdje se svi kutovi nalaze unutar slične orbite simetrije.
- Redovito. Ovo se primjenjuje tamo gdje je poligon i izotoksalan i izogonalan. Ekvivalentno je i jednakostraničan i ciklički ili i jednakostraničan i jednakostraničan. Zvjezdasti poligon je naziv koji se daje nekonveksnom mnogokutu koji je pravilan.
- Razno. Oni uključuju:
- Monotonija.
- Pravolinijski.
KUTOVI.
Dvije najčešće vrste kutova su unutarnji i vanjski kutovi.
- Unutarnji kut. Zbroj unutarnjih kutova za jednostavan n-kut je dan kao (n – 2) π radijana. Također se može dobiti za (n – 2) x 180 stupnjeva.
- Vanjski kut. To su dopunski kutovi kutovima u unutrašnjosti.
