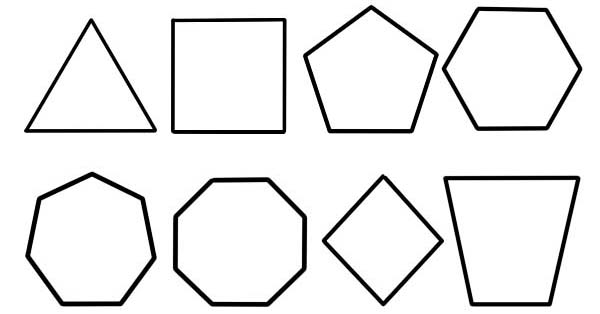
多角形は平面図形と呼ばれ、有限個の直線状の線分が接続されて閉じた多角形の連鎖または多角形の回路を形成することによって記述されます。境界回路、立体平面領域、または 2 つの組み合わせをポリゴンと呼ぶことができます。
多角形回路の要素は、そのエッジまたは側面と呼ばれることもあり、2 つのエッジの合流点は、多角形の角または頂点と呼ばれるものです。単数形では頂点と呼ばれます。ソリッド ポリゴンの内部は、その本体と呼ばれることがあります。 n 角形は、n 個の辺を持つ多角形に使用される用語です。例: 長方形は 4 角形です。
それ自体と交差しない多角形は、単純な多角形と言えます。数学者は主に単純な多角形からの多角形チェーンに関心を持っています。多角形の境界がそれ自体を横切ることができる場合、自己交差多角形と同様に星型多角形を形成することができます。
多角形は、任意の次元数のより一般的な多面体の 2 次元の例です。さまざまな目的のために定義された、さらに多くの多角形の一般化が存在します。
ポリゴンの分類。
ポリゴンはさまざまな方法で分類できます。それらの分類基準は次のとおりです。
- 辺の数。これは、ポリゴンの分類の主要かつ最も一般的なベースです。
- 凸と非凸。この下で、それらは次のようにサブグループ化できます。
- 凸。多角形を通り、境界線と 2 回交わる線。この結果、その内部のすべての角度は 180 °未満になります。
- 非凸。境界線と 2 回以上交わる可能性のある線。同様に、ポリゴンの外側を通る 2 つの境界点の間に線分が存在します。
- 凹面。これらは単純で非凸です。少なくとも 1 つの内角が 180度より大きい。
- 単純。ポリゴンの境界はそれ自体と交差しません。
- 星形。少なくとも一点から内部全体を見ることができます。
- スター ポリゴン。規則的に交差する多角形。
- 平等と対称性。
- 等角。すべての角度は等しい。 (コーナー角度)。
- 周期的。すべての角は、外接円と呼ばれる 1 つの円上にあります。
- 接線。これは、すべての辺が内接する円に接する場所です。
- 等辺。これは、すべての年齢が同じ長さを持つ場所です。
- 頂点推移的または等角。これは、すべてのコーナーが同様の対称軌道内にある場所です。
- 通常。これは、多角形が等角と等角の両方である場合に適用されます。同等に、それは等辺性と循環性の両方、または等角性と等辺性の両方です。スター ポリゴンは、凸でない正多角形に付けられた名前です。
- その他。それらには以下が含まれます:
角度。
最も一般的な 2 つのタイプの角度は、内角と外角です。
- 内角。単純な n 角形の内角の合計は、(n – 2) π ラジアンとして与えられます。 (n – 2) x 180 度でも得られます。
- 外角。これらは、内部の角度に対する補角です。
