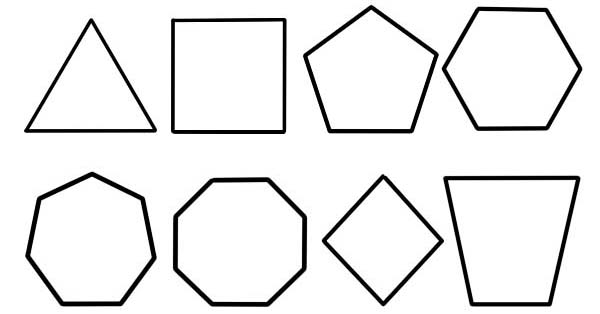
बहुभुजलाई एक समतल आकृति भनिन्छ जसको वर्णन सिधा रेखा खण्डहरूको सीमित संख्याद्वारा गरिन्छ जुन बन्द भएको बहुभुज श्रृंखला वा बहुभुज सर्किट बनाउन जोडिएको हुन्छ। बाउन्डिङ सर्किट, ठोस समतल क्षेत्र वा दुईको संयोजनलाई बहुभुज भन्न सकिन्छ।
बहुभुज सर्किटका तत्वहरूलाई यसको किनाराहरूमा उल्लेख गरिन्छ वा कहिलेकाँही पक्षहरूको रूपमा उल्लेख गरिन्छ, र दुई किनाराहरूको बैठक बिन्दुलाई बहुभुजको कुना वा ठाडोहरू भनिन्छ। यसको एकवचन रूप मा यो एक vertex को रूप मा उल्लेख गरिएको छ। ठोस बहुभुजको भित्री भागलाई कहिलेकाहीँ यसको शरीर भनिन्छ। एन-गोन एक शब्द हो जुन बहुभुजमा प्रयोग गरिन्छ जसको पक्षहरूको संख्या हुन्छ। उदाहरण को लागी: एक आयत एक 4-gon हो।
एक बहुभुज जसले आफैलाई प्रतिच्छेद गर्दैन एक साधारण बहुभुज भन्न सकिन्छ। गणितज्ञहरू प्रायः साधारण बहुभुजबाट बहुभुज चेनहरूसँग चिन्तित हुन्छन् जसले प्रायः बहुभुजलाई परिभाषित वा वर्णन गर्दछ। तारा बहुभुजका साथसाथै स्व-प्रतिच्छेदक बहुभुजहरू गठन हुन सक्छन् जहाँ बहुभुज सीमा आफैं पार गर्न अनुमति दिइन्छ।
बहुभुज कुनै पनि आयाम संख्यामा अधिक सामान्य पोलिटोपको २ आयामको उदाहरण हो। धेरै धेरै बहुभुजको सामान्यीकरणहरू अवस्थित छन् जुन विभिन्न उद्देश्यका लागि परिभाषित गरिएको छ।
बहुभुजहरूको वर्गीकरण।
बहुभुज धेरै फरक तरिकामा वर्गीकृत गर्न सकिन्छ। तिनीहरूको वर्गीकरणको आधारहरू समावेश छन्:
- पक्षहरूको संख्या। यो बहुभुजको वर्गीकरणको प्राथमिक र सबैभन्दा सामान्य आधार हो।
- उत्तल र गैर-उत्तलता। यस अन्तर्गत, तिनीहरूलाई उप-समूहमा विभाजन गर्न सकिन्छ:
- उत्तल। बहुभुज मार्फत कोरिएको कुनै पनि रेखा र सीमा दुई पटक मिल्छ। यसको नतिजाको रूपमा, यसको भित्री भागका सबै कोणहरू 180 0 भन्दा कम छन्।
- गैर-उत्तल। दुई पटक भन्दा बढी सिमाना मिल्न सक्ने रेखा। समान रूपमा, एक रेखा खण्ड दुई सीमा बिन्दुहरू बीच अवस्थित छ जुन बहुभुज बाहिर जान्छ।
- अवतल। यी सरल र गैर-उत्तल छन्। कम्तिमा एउटा भित्री कोण 180 0 भन्दा ठूलो छ।
- सरल। बहुभुजको सीमा आफैले पार गर्दैन।
- तारा आकारको। सम्पूर्ण भित्री भाग कम्तिमा एक बिन्दुबाट देख्न सकिन्छ।
- तारा बहुभुज। एक बहुभुज जसले आफैलाई नियमित रूपमा प्रतिच्छेद गर्दछ।
- समानता र समरूपता।
- समभुज। सबै कोण बराबर छन्। (कुना कोण)।
- चक्रीय। सबै कुनाहरू एउटै सर्कलमा बस्छन् जसलाई सर्कल भनिन्छ।
- स्पर्शिक। यो जहाँ सबै पक्षहरू एक वृत्त को स्पर्शरेखा हो जुन कुँदिएको छ।
- समभुज। यहाँ सबै उमेरका मानिसको लम्बाइ एउटै हुन्छ।
- वर्टेक्स ट्रान्जिटिव वा आइसोगोनल। यो जहाँ सबै कुनाहरू समान सममिति कक्षा भित्र विश्राम गर्दछ।
- नियमित। यो लागू हुन्छ जहाँ बहुभुज isotoxal र isogonal दुवै हुन्छ। समान रूपमा, यो समभुज र चक्रीय वा दुवै समभुज र समभुज हो। तारा बहुभुज एक गैर-उत्तल बहुभुजलाई दिइएको नाम हो जुन नियमित हुन्छ।
- विविध। तिनीहरू समावेश छन्:
एङ्गल्स।
दुई सबैभन्दा सामान्य प्रकारका कोणहरू भित्री र बाहिरी कोण हुन्।
- आन्तरिक कोण। साधारण n-gon को लागि भित्री कोणको योग (n – 2) π radians को रूपमा दिइएको छ। यो (n - 2) x 180 डिग्री द्वारा पनि प्राप्त गर्न सकिन्छ।
- बाहिरी कोण। यी भित्री कोणहरूमा पूरक कोणहरू हुन्।
