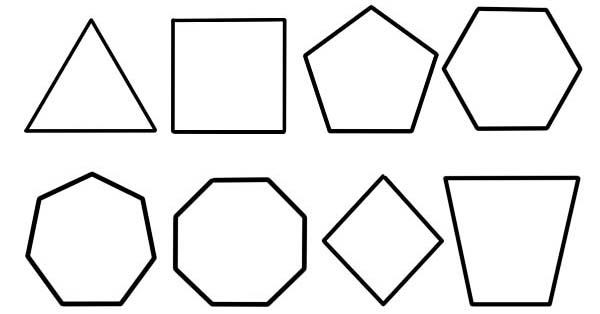
Um polígono é referido como uma figura plana cuja descrição é feita por um número finito de segmentos de reta que são conectados para formar uma cadeia poligonal que é fechada ou um circuito poligonal. O circuito delimitador, a região do plano sólido ou a combinação dos dois pode ser chamado de polígono.
Os elementos de um circuito poligonal são chamados de suas arestas ou às vezes chamados de lados, e o ponto de encontro de duas arestas é o que é chamado de canto ou vértices de um polígono. Na sua forma singular, é referido como um vértice. O interior de um polígono sólido às vezes é referido ao seu corpo. Um n-gon é um termo que é usado para um polígono que tem n número de lados. Por exemplo: um retângulo é um 4-gon.
Um polígono que não se intercepta pode ser considerado um polígono simples. Os matemáticos estão principalmente preocupados com as cadeias poligonais de polígonos simples que geralmente definem ou descrevem um polígono de acordo. Polígonos em estrela, bem como polígonos que se auto-intersectam, podem ser formados onde um limite poligonal pode cruzar-se.
Um polígono é um exemplo de um 2 dimensional do polytope mais comum em qualquer número de dimensão. Existem muitas outras generalizações de polígonos que são definidas para diferentes propósitos.
CLASSIFICAÇÃO DE POLÍGONOS.
Os polígonos podem ser classificados de muitas maneiras diferentes. Suas bases de classificação incluem:
- Número de lados. Esta é a base primária e mais comum de classificação de polígonos.
- Convexidade e não-convexidade. Sob isso, eles podem ser sub-agrupados em:
- Convexo. Qualquer linha que é desenhada através do polígono e encontra o limite duas vezes. Como resultado disso, todos os ângulos em seu interior são menores que 180 0 .
- Não convexo. Uma linha que pode encontrar o limite mais de duas vezes. De forma equivalente, existe um segmento de linha entre dois pontos de fronteira que passa fora do polígono.
- Côncavo. Estes são simples e não convexos. Pelo menos um ângulo interno é maior que 180 0 .
- Simples. O limite do polígono não se cruza.
- Em forma de estrela. Todo o interior pode ser visto de um ponto pelo menos.
- Polígono estrela. Um polígono que se intercepta de maneira regular.
- Igualdade e simetria.
- Equiângulo. Todos os ângulos são iguais. (ângulos de canto).
- Cíclico. Todos os cantos repousam em um único círculo que é chamado de circumcircle.
- Tangencial. Este é o lugar onde todos os lados são tangentes a um círculo que está inscrito.
- Equilátero. É aqui que todas as idades têm o mesmo comprimento.
- Vértice transitivo ou isogonal. Este é o lugar onde todos os cantos repousam dentro de uma órbita de simetria semelhante.
- Regular. Isso se aplica quando o polígono é isotoxal e isogonal. Equivalentemente, é equilátero e cíclico ou equiângulo e equilátero. Polígono estrela é o nome dado a um polígono não convexo que é regular.
- Diversos. Eles incluem:
ÂNGULOS.
Os dois tipos mais comuns de ângulos são os ângulos internos e externos.
- Ângulo interno. A soma dos ângulos internos para um n-gon simples é dada como (n – 2) π radianos. Também pode ser obtido por (n – 2) x 180 graus.
- Ângulo externo. São ângulos suplementares aos ângulos internos.
