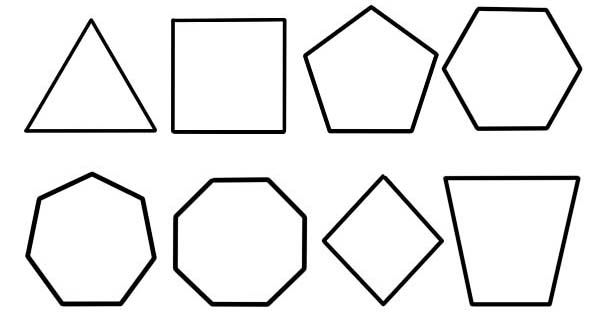
Многоугольник называется плоской фигурой, описание которой осуществляется с помощью конечного числа прямых отрезков, соединенных между собой, образуя замкнутую многоугольную цепь или многоугольную цепь. Ограничивающий контур, область сплошной плоскости или их комбинация могут называться многоугольником.
Элементы многоугольной схемы называются ее краями или иногда называются сторонами, а точка встречи двух ребер - это то, что называется углом или вершинами многоугольника. В особом виде он называется вершиной. Внутренность твердого многоугольника иногда называют его телом. N-угольник - это термин, который используется для обозначения многоугольника, имеющего n сторон. Например: прямоугольник - это 4-угольник.
Многоугольник, который не пересекает сам себя, можно назвать простым многоугольником. Математиков в основном интересуют многоугольные цепи из простых многоугольников, которые часто определяют или описывают многоугольник соответственно. Звездообразные многоугольники, а также самопересекающиеся многоугольники могут быть сформированы там, где многоугольная граница может пересекаться сама с собой.
Многоугольник - это пример двухмерного многогранника с любым размерным числом. Существует еще много обобщений многоугольника, которые определены для разных целей.
КЛАССИФИКАЦИЯ ПОЛИГОНОВ.
Полигоны можно классифицировать по-разному. Их основы классификации включают:
- Количество сторон. Это основная и самая распространенная база классификации полигонов.
- Выпуклость и невыпуклость. В соответствии с этим они могут быть разделены на:
- Выпуклый. Любая линия, проведенная через многоугольник и дважды пересекающая границу. В результате все углы внутри него меньше 180 0 .
- Невыпуклый. Линия, которая может встречаться с границей более двух раз. Точно так же между двумя граничными точками существует отрезок, который выходит за пределы многоугольника.
- Вогнутая. Они простые и невыпуклые. По крайней мере, один внутренний угол больше 180 ° .
- Простой. Граница многоугольника не пересекает себя.
- В форме звезды. Хотя бы с одной точки видно весь интерьер.
- Звездный многоугольник. Многоугольник, который регулярно пересекает себя.
- Равенство и симметрия.
- Равноугольный. Все углы равны. (угловые уголки).
- Циклический. Все углы опираются на один круг, называемый описанным кругом.
- Тангенциальный. Здесь все стороны касаются вписанной окружности.
- Равносторонний. Здесь все возрасты имеют одинаковую длину.
- Вершина транзитивна или изогональна. Здесь все углы лежат на одной и той же орбите симметрии.
- Обычный. Это применимо, когда многоугольник одновременно изотоксален и изогонален. Эквивалентно, он и равносторонний, и циклический, или равносторонний, и равносторонний. Звездный многоугольник - это имя, данное невыпуклому многоугольнику, который является правильным.
- Разнообразный. Они включают:
- Монотонный.
- Прямолинейный.
УГЛЫ.
Двумя наиболее распространенными типами углов являются внутренние и внешние углы.
- Внутренний угол. Сумма внутренних углов для простого n-угольника задается как (n - 2) π радиан. Его также можно получить под углом (n - 2) x 180 градусов.
- Внешний угол. Это дополнительные углы к углам в интерьере.
