รูปหลายเหลี่ยมเรียกว่ารูประนาบที่มีคำอธิบายโดยส่วนของเส้นตรงจำนวนหนึ่งที่เชื่อมต่อกันเพื่อสร้างห่วงโซ่รูปหลายเหลี่ยมที่ปิดหรือวงจรรูปหลายเหลี่ยม วงจรขอบเขต พื้นที่ระนาบทึบ หรือการรวมกันของทั้งสองสามารถเรียกได้ว่าเป็นรูปหลายเหลี่ยม
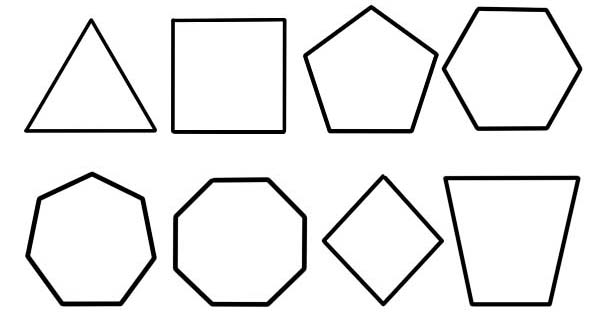
องค์ประกอบของวงจรหลายเหลี่ยมจะอ้างถึงขอบของมันหรือบางครั้งเรียกว่าด้าน และจุดบรรจบของสองขอบคือสิ่งที่เรียกว่ามุมหรือจุดยอดของรูปหลายเหลี่ยม ในรูปเอกพจน์เรียกว่าจุดยอด ภายในของรูปหลายเหลี่ยมที่เป็นของแข็งบางครั้งอ้างถึงร่างกายของมัน n-gon เป็นคำที่ใช้กับรูปหลายเหลี่ยมที่มีจำนวนด้าน n ด้าน ตัวอย่างเช่น สี่เหลี่ยมผืนผ้าคือ 4 เหลี่ยม
รูปหลายเหลี่ยมที่ไม่ตัดกันสามารถกล่าวได้ว่าเป็นรูปหลายเหลี่ยมธรรมดา นักคณิตศาสตร์ส่วนใหญ่เกี่ยวข้องกับสายโซ่รูปหลายเหลี่ยมจากรูปหลายเหลี่ยมธรรมดา ซึ่งมักจะกำหนดหรืออธิบายรูปหลายเหลี่ยมตามลำดับ รูปหลายเหลี่ยมรูปดาวและรูปหลายเหลี่ยมที่ตัดกันในตัวเองอาจก่อตัวขึ้นโดยอนุญาตให้ขอบรูปหลายเหลี่ยมตัดผ่านตัวมันเองได้
รูปหลายเหลี่ยมคือตัวอย่าง 2 มิติของโพลิโทปทั่วไปในจำนวนมิติใดๆ มีการวางนัยทั่วไปของรูปหลายเหลี่ยมอีกมากมายซึ่งกำหนดไว้เพื่อวัตถุประสงค์ที่แตกต่างกัน
การจำแนกประเภทของรูปหลายเหลี่ยม
รูปหลายเหลี่ยมสามารถจำแนกได้หลายวิธี พื้นฐานของการจัดประเภทประกอบด้วย:
- จำนวนด้าน นี่เป็นฐานหลักและฐานทั่วไปของการจำแนกรูปหลายเหลี่ยม
- ความนูนและไม่นูน ภายใต้นี้พวกเขาสามารถจัดกลุ่มย่อยเป็น:
- นูน เส้นใดๆ ที่ลากผ่านรูปหลายเหลี่ยมและบรรจบกับขอบเขตสองครั้ง ด้วยเหตุนี้มุมทั้งหมดภายในจึงน้อยกว่า 180 0 .
- ไม่นูน เส้นที่อาจพบเกินเขตแดนเกินสองครั้ง ในทำนองเดียวกัน ส่วนของเส้นตรงอยู่ระหว่างจุดขอบเขตสองจุดซึ่งผ่านนอกรูปหลายเหลี่ยม
- เว้า. สิ่งเหล่านี้เรียบง่ายและไม่นูน มุมภายในอย่างน้อยหนึ่งมุมมีค่ามากกว่า 180 0 .
- เรียบง่าย. ขอบเขตของรูปหลายเหลี่ยมไม่ตัดกัน
- รูปดาว. ภายในทั้งหมดสามารถมองเห็นได้จากจุดหนึ่งอย่างน้อย
- รูปหลายเหลี่ยมดาว รูปหลายเหลี่ยมที่ตัดกันตามปกติ
- ความเสมอภาคและสมมาตร
- เท่ากัน ทุกมุมเท่ากัน (มุมมุม).
- วัฏจักร มุมทั้งหมดวางอยู่บนวงกลมเดียวที่เรียกว่าวงกลม
- สัมผัส นี่คือจุดที่ทุกด้านเป็นสัมผัสของวงกลมที่จารึกไว้
- ด้านเท่ากันหมด นี่คือที่ที่ทุกวัยมีความยาวเท่ากัน
- จุดยอดสกรรมกริยาหรือภาพสามมิติ นี่คือจุดที่ทุกมุมอยู่ในวงโคจรสมมาตรที่คล้ายคลึงกัน
- ปกติ. สิ่งนี้ใช้กับรูปหลายเหลี่ยมที่เป็นทั้งไอโซทอกซอลและไอโซกอนอล เท่ากัน มันคือทั้งด้านเท่ากันหมดและวงจรหรือทั้งด้านเท่ากันหมดและด้านเท่ากันหมด รูปหลายเหลี่ยมรูปดาวคือชื่อที่กำหนดให้กับรูปหลายเหลี่ยมที่ไม่นูนซึ่งปกติ
- เบ็ดเตล็ด. พวกเขารวมถึง:
มุม
มุมที่พบบ่อยที่สุดสองประเภทคือมุมภายในและภายนอก
- มุมภายใน. ผลรวมของมุมภายในสำหรับ n-gon ธรรมดาจะได้รับเป็น (n – 2) π เรเดียน นอกจากนี้ยังสามารถรับได้ (n – 2) x 180 องศา
- มุมภายนอก. เหล่านี้เป็นมุมเสริมของมุมภายใน
