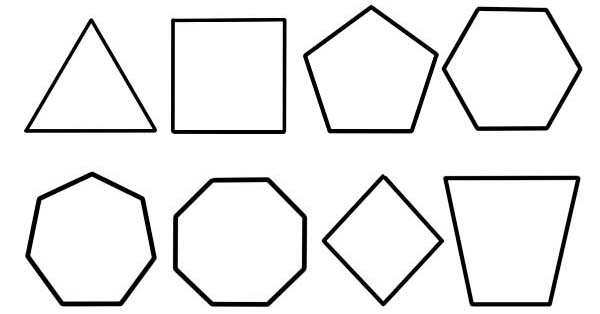
Полігоном називають плоску фігуру, опис якої здійснюється за допомогою кінцевої кількості прямолінійних відрізків, які з’єднані, утворюючи багатокутний ланцюг, який є замкненим, або багатокутний ланцюг. Обмежувальний контур, область суцільної площини або їх поєднання можна назвати багатокутником.
Елементи багатокутної схеми називаються її ребрами або іноді їх називають сторонами, а точка зустрічі двох ребер - це те, що називається кутом чи вершиною багатокутника. У своїй однинній формі його називають вершиною. Інтер'єр твердого багатокутника іноді називають його тілом. N-кутник - це термін, який використовується для багатокутника, що має n кількість сторін. Наприклад: прямокутник - це 4-кутник.
Багатокутник, який не перетинається сам, можна сказати простим многокутником. Математики здебільшого стурбовані полігональними ланцюгами з простих багатокутників, які часто визначають або описують багатокутник відповідно. Зіркові багатокутники, а також самоперетинаються багатокутники можуть утворюватися там, де дозволено перетинатись полігональній межі.
Багатокутник - це приклад двовимірного розповсюдженого багатогранника в будь-якому розмірному числі. Існує набагато більше узагальнень багатокутників, які визначені для різних цілей.
КЛАСИФІКАЦІЯ ПОЛІГОНІВ.
Полігони можна класифікувати різними способами. Їх основи класифікації включають:
- Кількість сторін. Це основна і найпоширеніша база класифікації багатокутників.
- Опуклість і неопуклість. Під цим їх можна підгрупувати на:
- Опуклий. Будь-яка лінія, яка проведена через багатокутник і двічі відповідає межі. В результаті цього всі кути у його внутрішній частині становлять менше 180 0 .
- Неопуклий. Лінія, яка може бути знайдена так, щоб вона відповідала межі більше двох разів. Як і рівноцінно, між двома граничними точками, що виходить за межі багатокутника, існує відрізок.
- Увігнутий. Це прості і не опуклі. Принаймні один внутрішній кут більше 180 0 .
- Простий. Межа багатокутника не перетинається сама.
- Зіркоподібна. Весь інтер’єр можна побачити принаймні з однієї точки.
- Зірковий багатокутник. Багатокутник, який регулярно перетинається.
- Рівність і симетрія.
- Рівнокутна. Всі кути рівні. (кутові кути).
- Циклічний. Всі кути опираються на єдине коло, яке називають описаним колом.
- Дотичний. Тут всі сторони є дотичною до кола, яке вписано.
- Рівносторонній. Тут всі віки мають однакову довжину.
- Вершина перехідна або ізогональна. Тут всі кути розташовані в межах подібної орбіти симетрії.
- Регулярні. Це стосується тих випадків, коли багатокутник одночасно є ізотоксальним та ізогональним. Як і рівноцінно, він одночасно рівносторонній і циклічний, або рівнокутний і рівносторонній. Зірковий багатокутник - це назва, що має невипуклий багатокутник, регулярний.
- Різне. Вони включають:
- Одноманітність.
- Прямолінійна.
КУТИ.
Два найпоширеніші типи кутів - це внутрішній та зовнішній кути.
- Внутрішній кут. Сума внутрішніх кутів для простого n-кутника дається як (n - 2) π радіанів. Його також можна отримати на (n - 2) x 180 градусів.
- Зовнішній кут. Це додаткові кути до кутів у інтер’єрі.
