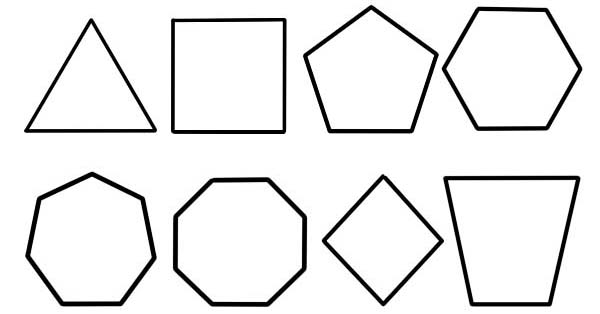
ایک کثیر الاضلاع کو ہوائی جہاز کے اعداد و شمار کے طور پر کہا جاتا ہے جس کی تفصیل سیدھے سیدھے سیدھے خطوں کی ایک محدود تعداد کے ذریعہ کی جاتی ہے جو ایک متعدد زنجیر کی شکل سے منسلک ہوتا ہے جو بند ہے یا ایک کثیرالضحی سرکٹ ہے۔ باؤنڈنگ سرکٹ ، ٹھوس طیارے کا خطہ یا دونوں کے امتزاج کو کثیرالاضلاع کہا جاسکتا ہے۔
ایک کثیرالضحی سرکٹ کے عناصر کو اس کے کناروں کا حوالہ دیا جاتا ہے یا بعض اوقات اطراف کے طور پر بھیجا جاتا ہے ، اور دو کناروں کا میٹنگ پوائنٹ وہی ہوتا ہے جس کو کثیرالاضلاع کونے یا افقی طور پر حوالہ دیا جاتا ہے۔ اس کی واحد شکل میں اسے محور کے طور پر جانا جاتا ہے۔ ایک ٹھوس کثیرالاضلاع کا داخلہ بعض اوقات اس کے جسم کو بھیجا جاتا ہے۔ این-گون ایک اصطلاح ہے جو کثیرالاضلاع کے لئے استعمال ہوتی ہے جس کے اطراف کی تعداد تعداد ہوتی ہے۔ مثال کے طور پر: ایک مستطیل 4 گون ہے۔
ایک کثیرالاضلہ جو اپنے آپ کو آپس میں نہیں جوڑتا ہے اسے ایک سادہ کثیرالاثلہ کہا جاسکتا ہے۔ ریاضی کے ماہر زیادہ تر عام کثیرالاضلہ کی کثیر زنجیروں سے تعلق رکھتے ہیں جو اکثر کثیرالاضحی کی وضاحت یا اس کے مطابق وضاحت کرتے ہیں۔ اسٹار کثیر القائد کے ساتھ ساتھ خود سے متعل .ق کثیر القائد بھی تشکیل پاسکتے ہیں جہاں کثیرالاضحی حدود کو خود کو عبور کرنے کی اجازت ہے۔
کثیرالاضلاع کسی بھی طول و عرض کی تعداد میں زیادہ عام پولیٹوپ کے 2 جہتی کی ایک مثال ہے۔ کثیرالاضلاع کی بہت سی عمومی حیثیتیں موجود ہیں جو مختلف مقاصد کے لئے بیان کی گئی ہیں۔
پولیگان کی درجہ بندی۔
کثیرالاضلاع کو کئی مختلف طریقوں سے درجہ بندی کیا جاسکتا ہے۔ ان کی درجہ بندی کے اڈوں میں شامل ہیں:
- اطراف کی تعداد یہ کثیرالاضلاع کی درجہ بندی کا بنیادی اور سب سے عام اڈہ ہے۔
- محرک اور غیر محرک اس کے تحت ، ان کو ذیلی گروپ کیا جاسکتا ہے:
- محدب کوئی بھی لائن جو کثیرالاضلاع کے ذریعے کھینچی جاتی ہے اور دو بار حد سے ملتی ہے۔ اس کے نتیجے میں ، اس کے داخلہ کے تمام زاویے 180 0 سے کم ہیں۔
- غیر محدب ایک لائن جو دو بار سے زیادہ حد کو ملنے کے لئے مل سکتی ہے۔ مساوی طور پر ، دو حدود کے درمیان ایک قطعہ موجود ہے جو کثیرالاضلاع کے باہر سے گزرتا ہے۔
- Concave. یہ آسان اور غیر محدب ہیں۔ کم از کم ایک داخلہ زاویہ 180 0 سے زیادہ ہے۔
- آسان کثیرالاضلاع کی حدود خود کو عبور نہیں کرتی ہے۔
- ستارے کی شکل کا کم سے کم ایک نقطہ نظر سے پورا داخلہ دیکھا جاسکتا ہے۔
- ستارہ کثیرالاضلاع۔ ایک کثیرالاضلاع جو باقاعدگی سے اپنے آپ کو ایک دوسرے سے جدا کرتا ہے۔
- مساوات اور توازن۔
- مساوات تمام زاویے برابر ہیں۔ (کونے کونے)
- چکرا تمام کونے ایک ہی دائرے پر آرام کرتے ہیں جسے ختنوں کے نام سے موسوم کیا جاتا ہے۔
- ٹینجینٹل یہ وہ جگہ ہے جہاں سارے اطراف ایک دائرے کے لئے ٹینجینٹ ہیں جو لکھا ہوا ہے۔
- یکطرفہ۔ یہ وہ جگہ ہے جہاں تمام عمر کی لمبائی ایک جیسی ہوتی ہے۔
- عمودی عارضی یا الگ الگ۔ یہ وہ جگہ ہے جہاں تمام کونے ملتے جلتے توازن کے مدار میں رہتے ہیں۔
- باقاعدہ۔ یہ لاگو ہوتا ہے جہاں کثیر الاضلاع آاسوٹوکسل اور آاسوگونل دونوں ہیں۔ مساویانہ طور پر ، یہ باہمی اور چکریی یا دونوں ہی مساوات اور ہم آہنگ ہے۔ اسٹار کثیر الاضلاع نام ہے جس میں ایک غیر محدب کثیر الاضلاع کو دیا جاتا ہے جو باقاعدہ ہوتا ہے۔
- متفرق. ان میں شامل ہیں:
اینگلز
دو عام قسم کے زاویے داخلہ اور بیرونی زاویے ہیں۔
- داخلہ زاویہ۔ داخلی زاویوں کی ایک سادہ این نون کے لئے رقم (n - 2) π ریڈین دی جاتی ہے۔ یہ (n - 2) x 180 ڈگری کے ذریعہ بھی حاصل کیا جاسکتا ہے۔
- بیرونی زاویہ یہ اندرونی زاویوں کے ضمنی زاویے ہیں۔
