الانحراف يعني مدى البعد عن المعدل الطبيعي أو المتوسط.
يمكننا استخدام الانحراف المعياري لمعرفة ما إذا كان سلوك معين طبيعيًا أم فريدًا / غير عادي. غالبًا ما يتم حساب الانحراف المعياري باستخدام متوسط مجموعة البيانات ، ويساعدنا ذلك في معرفة مدى انتشار البيانات. بعبارة أخرى ، في مجموعة من البيانات ، يخبرنا الانحراف المعياري عن مدى إحكام تجميع جميع نقاط البيانات المختلفة حول المتوسط. يُشار إلى الانحراف المعياري بالرمز \('\sigma'\) .
يمكن بسهولة حساب الانحراف المعياري باستخدام الآلة الحاسبة أو برنامج جداول البيانات أو الصيغ الرياضية الموضحة أدناه.
لنأخذ مثالاً لفهمه بشكل أفضل. دعونا نأخذ في الاعتبار عدد الفاكهة التي يمتلكها جيرانك في منازلهم.
| الجار | عدد الفاكهة (X) |
| سام | 3 |
| دانيال | 4 |
| روبن | 6 |
| ماري | 7 |
| كيم | 9 |
عدد الثمار عبارة عن نقاط بيانات يُشار إليها بعلامة x ويتم تمثيل المتوسط بواسطة \(\bar{x}\) . يعني بالنسبة للبيانات أعلاه
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
شكّل الآن جدولاً يعرض نقاط البيانات ( \(x\) ) ، والمتوسط ( \(\bar{x}\) ) واختلاف نقطة البيانات عن الوسط ( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
أوجد متوسط الفروق \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
الانحراف المعياري:
\(\sigma = \sqrt{4.56} = 2.13\)
يعني = 5.8 فواكه
الانحراف المعياري = 2.13 فاكهة
الآن يمكننا بسهولة معرفة من هم ضمن انحراف معياري واحد ومن هم وراءه. لذا يساعدنا الانحراف المعياري في معرفة الحالات الطبيعية وما هي الحالات الاستثنائية.
يمكننا أن نتوقع أن يقع حوالي ثلثي البيانات ضمن الانحراف المعياري +1 أو -1 عن المتوسط. يمكننا أن نقول \(\frac{2}{3}^{rd}\) لدى الجيران ما بين 7.93 (5.8 + 2.13) و 3.67 (5.8 - 2.13) في منازلهم.
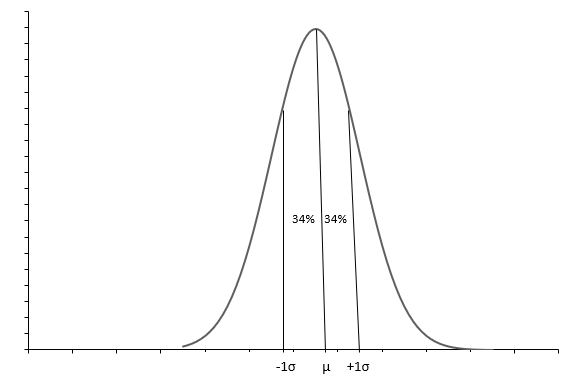
يوضح الرسم البياني أعلاه توزيعًا طبيعيًا بمنحنى شكل الجرس. يتم تعريف كل توزيع عادي بالمتوسط ( \(\mu\) ) والانحراف المعياري ( \(\sigma\) ). ما يقرب من 68٪ من الملاحظات تقع بين \(+1\sigma\) و \(-1\sigma\) . يخبرنا المتوسط ( \(\mu\) ) أيضًا الوسيط بنقطة منتصف التوزيع ، والتي تنتشر حولها جميع قيم البيانات. الانحراف المعياري ( \(\sigma\) ) يخبرنا عن كيفية نشر البيانات.
لحساب الانحراف المعياري اتبع الخطوات التالية:
1) ابحث عن المتوسط ( \(\bar{x}\) ) لعناصر البيانات في المجموعة المحددة
2) خذ كل اختلاف في عنصر البيانات من المتوسط ، وقم بتربيعه ، ثم متوسط النتيجة. هذه النتيجة تسمى التباين
3) خذ الجذر التربيعي للتباين ، وهذا سيعطي الانحراف المعياري \(\sigma\)