Sapma normadan və ya ortadan nə qədər uzaq olduğunu bildirir.
Müəyyən davranışın normal və ya unikal/fövqəladə olduğunu bilmək üçün standart sapmadan istifadə edə bilərik. Standart sapma çox vaxt verilənlər dəstinin ortası ilə hesablanır və bu, bizə məlumatların necə yayıldığını bilməyə kömək edir. Başqa sözlə, verilənlər toplusunda standart sapma bizə bütün müxtəlif məlumat nöqtələrinin orta ətrafında nə qədər sıx birləşdiyini bildirir. Standart sapma \('\sigma'\) simvolu ilə işarələnir.
Standart kənarlaşma asanlıqla kalkulyator, cədvəl proqramı və ya aşağıda izah edilən riyaziyyat düsturlarından istifadə etməklə hesablana bilər.
Bunu daha yaxşı başa düşmək üçün bir misal çəkək. Qonşularınızın evlərində olan meyvələrin sayını nəzərə alaq.
| Qonşu | meyvələrin sayı ( X) |
| Sam | 3 |
| Daniel | 4 |
| Robin | 6 |
| Məryəm | 7 |
| Kim | 9 |
Meyvələrin sayı x ilə işarələnən məlumat nöqtələridir və Orta \(\bar{x}\) ilə təmsil olunur. Yuxarıdakı məlumatlar üçün ortadır
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
İndi məlumat nöqtələrini ( \(x\) ) , orta ( \(\bar{x}\) ) və məlumat nöqtəsinin orta ( \(x - \bar{x}\) ) ilə fərqini göstərən cədvəl yaradın.
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Fərqlərin ortasını tapın \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Standart sapma:
\(\sigma = \sqrt{4.56} = 2.13\)
Orta = 5,8 meyvə
Standart sapma = 2.13 meyvə
İndi kimin bir standart sapma daxilində olduğunu və kimin ondan kənarda olduğunu asanlıqla anlaya bilərik. Beləliklə, standart sapma bizə nəyin normal, nəyin qeyri-adi hallar olduğunu bilməyə kömək edir.
Məlumatların təxminən üçdə ikisinin ortadan +1 və ya -1 standart kənara çıxmasını gözləyə bilərik. Qonşuların \(\frac{2}{3}^{rd}\) evlərində 7,93(5,8 + 2,13) ilə 3,67 (5,8 - 2,13) arasında meyvə olduğunu deyə bilərik.
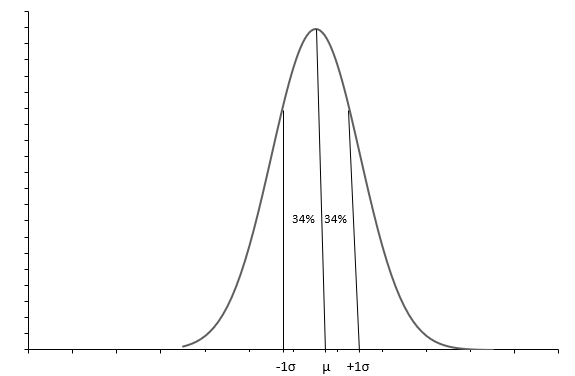
Yuxarıdakı qrafik zəng formalı əyri ilə normal paylanmanı göstərir. Hər Normal paylama orta ( \(\mu\) ) və standart sapma ( \(\sigma\) ) ilə müəyyən edilir. Müşahidələrin təxminən 68%-i \(+1\sigma\) və \(-1\sigma\) arasındadır. Orta ( \(\mu\) ) eyni zamanda median bizə paylanmanın orta nöqtəsini bildirir, ətrafda bütün məlumat qiymətləri yayılır. Standart sapma ( \(\sigma\) ) bizə məlumatın necə yayılacağını izah edir.
Standart sapmanı hesablamaq üçün aşağıdakı addımları yerinə yetirin:
1) Verilmiş çoxluqdakı məlumat elementlərinin ortasını ( \(\bar{x}\) ) tapın
2) Məlumat elementinin hər bir fərqini ortadan götürün, kvadratını alın və nəticəni ortalayın. Bu nəticə Variasiya adlanır
3) Variasiyanın kvadrat kökünü götürün, bu Standart Sapma \(\sigma\) verəcəkdir.