বিচ্যুতি মানে স্বাভাবিক বা গড় থেকে কত দূরে।
নির্দিষ্ট আচরণ স্বাভাবিক বা অনন্য/অসাধারণ কিনা তা জানতে আমরা আদর্শ বিচ্যুতি ব্যবহার করতে পারি। স্ট্যান্ডার্ড বিচ্যুতি প্রায়শই একটি ডেটা সেটের গড় দিয়ে গণনা করা হয় এবং এটি আমাদের জানতে সাহায্য করে যে ডেটা কীভাবে ছড়িয়ে পড়ে। অন্য কথায়, ডেটার একটি সেটে স্ট্যান্ডার্ড বিচ্যুতি আমাদের বলে যে কতটা শক্তভাবে সমস্ত বিভিন্ন ডেটা পয়েন্ট গড়ের চারপাশে ক্লাস্টার করা হয়েছে। প্রমিত বিচ্যুতি \('\sigma'\) চিহ্ন দ্বারা চিহ্নিত করা হয়।
স্ট্যান্ডার্ড বিচ্যুতি সহজেই একটি ক্যালকুলেটর, স্প্রেডশীট সফ্টওয়্যার বা গণিত সূত্র ব্যবহার করে গণনা করা যেতে পারে যা নীচে ব্যাখ্যা করা হয়েছে।
এটি আরও ভালভাবে বোঝার জন্য একটি উদাহরণ দেওয়া যাক। আসুন আপনার প্রতিবেশীদের বাড়িতে কতগুলি ফল রয়েছে তার হিসাব নেওয়া যাক।
| প্রতিবেশী | ফলের সংখ্যা (X) |
| স্যাম | 3 |
| ড্যানিয়েল | 4 |
| রবিন | 6 |
| মেরি | 7 |
| কিম | 9 |
ফলের সংখ্যা হল ডেটা পয়েন্ট যা x দ্বারা চিহ্নিত করা হয় এবং গড়কে \(\bar{x}\) দ্বারা প্রকাশ করা হয়। উপরোক্ত তথ্যের জন্য গড়
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
এখন একটি টেবিল তৈরি করুন যা ডেটা পয়েন্ট ( \(x\) ) , গড় ( \(\bar{x}\) ) এবং গড় থেকে ডেটা পয়েন্টের পার্থক্য দেখায়( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | ৫.৮ | 7.84 |
| 4 | ৫.৮ | 3.24 |
| 6 | ৫.৮ | 0.04 |
| 7 | ৫.৮ | 1.44 |
| 9 | ৫.৮ | 10.24 |
পার্থক্যের গড় নির্ণয় কর \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
আদর্শ চ্যুতি:
\(\sigma = \sqrt{4.56} = 2.13\)
গড় = 5.8 ফল
আদর্শ বিচ্যুতি = 2.13 ফল
এখন আমরা সহজেই বের করতে পারি কারা এক আদর্শ বিচ্যুতির মধ্যে এবং কারা এর বাইরে। সুতরাং আদর্শ বিচ্যুতি আমাদের জানতে সাহায্য করে যে কোনটি সাধারণ কেস এবং কোনটি অসাধারণ কেস।
আমরা আশা করতে পারি প্রায় দুই-তৃতীয়াংশ ডেটা গড় থেকে +1 বা -1 স্ট্যান্ডার্ড বিচ্যুতির মধ্যে পড়বে। আমরা বলতে পারি প্রতিবেশীদের \(\frac{2}{3}^{rd}\) তাদের বাড়িতে 7.93 (5.8 + 2.13) এবং 3.67 (5.8 - 2.13) ফল রয়েছে৷
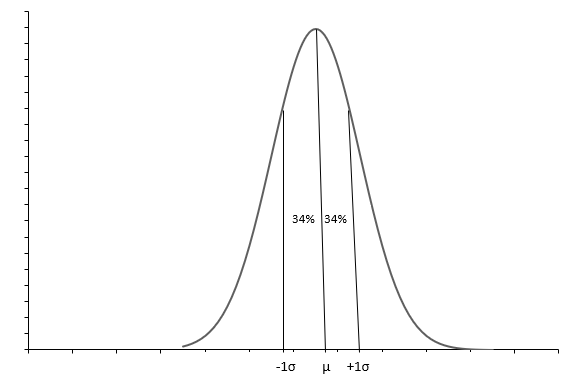
উপরের গ্রাফটি একটি বেল আকৃতির বক্ররেখা সহ একটি স্বাভাবিক বন্টন দেখায়। প্রতিটি সাধারণ বন্টন গড় ( \(\mu\) ) এবং মানক বিচ্যুতি ( \(\sigma\) ) দিয়ে সংজ্ঞায়িত করা হয়। প্রায় 68% পর্যবেক্ষণ \(+1\sigma\) এবং \(-1\sigma\) মধ্যে পড়ে। গড়( \(\mu\) ) এছাড়াও মধ্যমা আমাদেরকে বন্টনের মধ্য-বিন্দু বলে, যার চারপাশে সমস্ত ডেটা মান ছড়িয়ে আছে। স্ট্যান্ডার্ড ডেভিয়েশন( \(\sigma\) ) আমাদের বলে যে কীভাবে ডেটা ছড়িয়ে দিতে হয়।
আদর্শ বিচ্যুতি গণনা করতে নিম্নলিখিত পদক্ষেপগুলি অনুসরণ করুন:
1) প্রদত্ত সেটে ডেটা আইটেমগুলির গড় ( \(\bar{x}\) ) খুঁজুন
2) গড় থেকে ডেটা আইটেমের প্রতিটি পার্থক্য নিন, এটিকে বর্গ করুন এবং তারপর ফলাফল গড় করুন। এই ফলাফলকে ভ্যারিয়েন্স বলা হয়
3) ভ্যারিয়েন্সের বর্গমূল নিন, এটি মানক বিচ্যুতি দেবে \(\sigma\)