Abweichung bedeutet, wie weit vom Normalwert oder Durchschnitt entfernt.
Wir können die Standardabweichung verwenden, um festzustellen, ob ein bestimmtes Verhalten normal oder einzigartig/außergewöhnlich ist. Die Standardabweichung wird oft mit dem Mittelwert eines Datensatzes berechnet und hilft uns zu wissen, wie verteilt die Daten sind. Mit anderen Worten, in einer Reihe von Daten sagt uns die Standardabweichung, wie eng alle verschiedenen Datenpunkte um den Mittelwert gruppiert sind. Die Standardabweichung wird durch das Symbol \('\sigma'\) bezeichnet.
Die Standardabweichung kann einfach mit einem Taschenrechner, einer Tabellenkalkulationssoftware oder mathematischen Formeln berechnet werden, die unten erklärt werden.
Nehmen wir ein Beispiel, um es besser zu verstehen. Berücksichtigen wir die Anzahl der Früchte, die Ihre Nachbarn in ihren Häusern haben.
| Nachbar | Anzahl Früchte ( X) |
| Sam | 3 |
| Daniel | 4 |
| Robin | 6 |
| Maria | 7 |
| Kim | 9 |
Die Anzahl der Früchte sind Datenpunkte, die mit x bezeichnet werden und der Mittelwert wird durch \(\bar{x}\) dargestellt. Mittelwert für die obigen Daten ist
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Bilden Sie nun eine Tabelle, die Datenpunkte ( \(x\) ) , Mittelwert ( \(\bar{x}\) und Differenz des Datenpunkts vom Mittelwert ( \(x - \bar{x}\) zeigt.
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0,04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 24.10 |
Finden Sie den Mittelwert der Differenzen \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Standardabweichung:
\(\sigma = \sqrt{4.56} = 2.13\)
Durchschnitt = 5,8 Früchte
Standardabweichung = 2,13 Früchte
Jetzt können wir leicht herausfinden, wer innerhalb einer Standardabweichung liegt und wer darüber hinaus. Die Standardabweichung hilft uns also zu wissen, was normale Fälle und was außergewöhnliche Fälle sind.
Wir können davon ausgehen, dass etwa zwei Drittel der Daten innerhalb einer Standardabweichung von +1 oder -1 vom Mittelwert liegen. Wir können sagen \(\frac{2}{3}^{rd}\) der Nachbarn zwischen 7,93 (5,8 + 2,13) und 3,67 (5,8 - 2,13) Früchte in ihren Häusern haben.
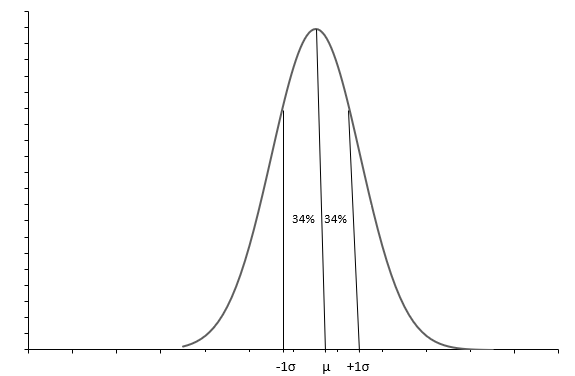
Das obige Diagramm zeigt eine Normalverteilung mit einer glockenförmigen Kurve. Jede Normalverteilung wird mit dem Mittelwert ( \(\mu\) ) und der Standardabweichung ( \(\sigma\) ) definiert. Etwa 68 % der Beobachtungen liegen zwischen \(+1\sigma\) und \(-1\sigma\) . Der Mittelwert ( \(\mu\) ) auch der Median gibt uns den Mittelpunkt der Verteilung an, um den alle Datenwerte verteilt sind. Die Standardabweichung ( \(\sigma\) ) sagt uns, wie die Daten zu verteilen sind.
Führen Sie die folgenden Schritte aus, um die Standardabweichung zu berechnen:
1) Finden Sie den Mittelwert ( \(\bar{x}\) ) der Datenelemente in der gegebenen Menge
2) Nehmen Sie jede Differenz der Datenelemente vom Mittelwert, quadrieren Sie sie und mitteln Sie dann das Ergebnis. Dieses Ergebnis wird Varianz genannt
3) Nehmen Sie die Quadratwurzel der Varianz, dies ergibt die Standardabweichung \(\sigma\)