Desviación significa qué tan lejos de lo normal o promedio.
Podemos usar la desviación estándar para saber si cierto comportamiento es normal o único/extraordinario. La desviación estándar a menudo se calcula con la media de un conjunto de datos y nos ayuda a saber qué tan dispersos están los datos. En otras palabras, en un conjunto de datos, la desviación estándar nos dice qué tan estrechamente se agrupan todos los puntos de datos alrededor de la media. La desviación estándar se indica con el símbolo \('\sigma'\) .
La desviación estándar se puede calcular fácilmente usando una calculadora, un software de hoja de cálculo o fórmulas matemáticas que se explican a continuación.
Pongamos un ejemplo para entenderlo mejor. Tomemos en cuenta la cantidad de frutas que tienen tus vecinos en sus casas.
| Vecino | Nº de frutos (X) |
| Sam | 3 |
| Daniel | 4 |
| Robin | 6 |
| María | 7 |
| Kim | 9 |
El número de frutas son puntos de datos que se indican con x y la media se representa con \(\bar{x}\) . La media de los datos anteriores es
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Ahora forme una tabla que muestre los puntos de datos ( \(x\) ), la media ( \(\bar{x}\) ) y la diferencia entre el punto de datos y la media ( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Encuentra la media de las diferencias \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Desviación Estándar:
\(\sigma = \sqrt{4.56} = 2.13\)
Media = 5,8 frutos
Desviación Estándar = 2.13 frutos
Ahora podemos averiguar fácilmente quiénes están dentro de una desviación estándar y quiénes están más allá. Entonces, la desviación estándar nos ayuda a saber qué son casos normales y qué casos extraordinarios.
Podemos esperar que alrededor de dos tercios de los datos se encuentren dentro de una desviación estándar de +1 o -1 de la media. Podemos decir \(\frac{2}{3}^{rd}\) de vecinos tienen entre 7.93(5.8 + 2.13) y 3.67 (5.8 - 2.13) frutas en sus casas.
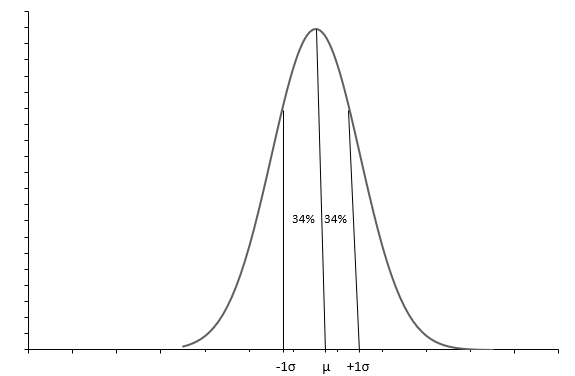
El gráfico anterior muestra una distribución normal con una curva en forma de campana. Cada distribución normal se define con la media ( \(\mu\) ) y la desviación estándar ( \(\sigma\) ). Aproximadamente el 68 % de las observaciones se encuentran entre \(+1\sigma\) y \(-1\sigma\) . La media( \(\mu\) ) también la mediana nos dice el punto medio de la distribución, alrededor del cual se distribuyen todos los valores de los datos. La desviación estándar ( \(\sigma\) ) nos dice cómo distribuir los datos.
Para calcular la desviación estándar, siga los pasos a continuación:
1) Encuentra la media ( \(\bar{x}\) ) de los elementos de datos en el conjunto dado
2) Tome cada diferencia de elemento de datos de la media, elévela al cuadrado y luego promedie el resultado. Este resultado se llama Varianza.
3) Saque la raíz cuadrada de la varianza, esto le dará la desviación estándar \(\sigma\)