انحراف به این معنی است که چقدر از حد معمول یا متوسط فاصله دارد.
ما میتوانیم از انحراف معیار استفاده کنیم تا بدانیم آیا رفتار خاصی طبیعی است یا منحصربهفرد/غیرعادی. انحراف استاندارد اغلب با میانگین یک مجموعه داده محاسبه میشود و به ما کمک میکند تا بدانیم دادهها چقدر پراکنده هستند. به عبارت دیگر، در مجموعهای از دادهها، انحراف استاندارد به ما میگوید که چگونه تمام نقاط داده مختلف حول میانگین خوشهبندی شدهاند. انحراف استاندارد با نماد \('\sigma'\) نشان داده می شود.
انحراف معیار را می توان به راحتی با استفاده از یک ماشین حساب، نرم افزار صفحه گسترده یا فرمول های ریاضی که در زیر توضیح داده شده است محاسبه کرد.
برای درک بهتر، مثالی می زنیم. بیایید به تعداد میوه هایی که همسایه های شما در خانه هایشان دارند حساب کنیم.
| همسایه | تعداد میوه ها (X) |
| سام | 3 |
| دانیال | 4 |
| رابین | 6 |
| مريم | 7 |
| کیم | 9 |
تعداد میوه ها نقاط داده ای هستند که با x نشان داده می شوند و میانگین با \(\bar{x}\) نشان داده می شود. میانگین برای داده های فوق است
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
اکنون جدولی تشکیل دهید که نقاط داده ( \(x\) ) ، میانگین ( \(\bar{x}\) ) و تفاوت نقطه داده از میانگین \(x - \bar{x}\) نشان می دهد.
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
میانگین تفاوتها را بیابید \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
انحراف معیار:
\(\sigma = \sqrt{4.56} = 2.13\)
میانگین = 5.8 میوه
انحراف استاندارد = 2.13 میوه
اکنون ما به راحتی می توانیم بفهمیم که چه کسانی در یک انحراف معیار قرار دارند و چه کسانی فراتر از آن هستند. بنابراین انحراف معیار به ما کمک می کند تا بدانیم چه مواردی عادی و چه مواردی غیرعادی هستند.
ما می توانیم انتظار داشته باشیم که حدود دو سوم داده ها در انحراف استاندارد +1 یا -1 از میانگین قرار گیرند. می توان گفت \(\frac{2}{3}^{rd}\) همسایگان بین 7.93 (5.8 + 2.13) و 3.67 (5.8 - 2.13) میوه در خانه های خود دارند.
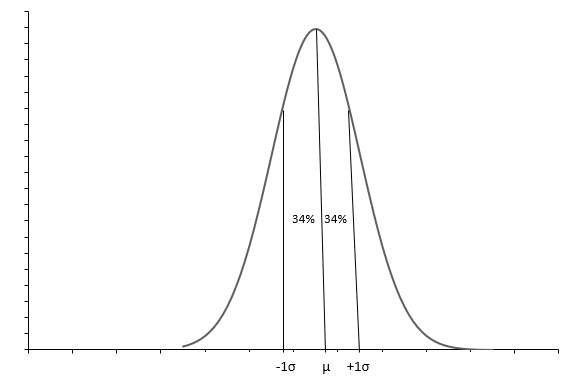
نمودار بالا توزیع نرمال را با منحنی زنگوله ای نشان می دهد. هر توزیع نرمال با میانگین ( \(\mu\) ) و انحراف استاندارد ( \(\sigma\) تعریف می شود. تقریباً 68٪ از مشاهدات بین \(+1\sigma\) و \(-1\sigma\) قرار دارند. میانگین ( \(\mu\) ) همچنین میانه نقطه میانی توزیع را به ما می گوید که تمام مقادیر داده ها در اطراف آن پخش می شوند. انحراف استاندارد( \(\sigma\) ) به ما می گوید که چگونه داده ها را پخش کنیم.
برای محاسبه انحراف معیار مراحل زیر را دنبال کنید:
1) میانگین ( \(\bar{x}\) اقلام داده در مجموعه داده شده را بیابید
2) هر تفاوت آیتم داده را از میانگین بگیرید، مربع آن را بگیرید و سپس میانگین نتیجه را بگیرید. این نتیجه واریانس نامیده می شود
3) ریشه دوم واریانس را بگیرید، این انحراف استاندارد \(\sigma\) نشان می دهد.