L'écart signifie à quelle distance de la normale ou de la moyenne.
Nous pouvons utiliser l'écart type pour savoir si certains comportements sont normaux ou uniques/extraordinaires. L'écart type est souvent calculé avec la moyenne d'un ensemble de données, et cela nous aide à savoir dans quelle mesure les données sont réparties. En d'autres termes, dans un ensemble de données, l'écart type nous indique à quel point tous les différents points de données sont regroupés autour de la moyenne. L'écart type est indiqué par le symbole \('\sigma'\) .
L'écart type peut facilement être calculé à l'aide d'une calculatrice, d'un tableur ou de formules mathématiques expliquées ci-dessous.
Prenons un exemple pour mieux comprendre. Tenons compte du nombre de fruits que vos voisins ont chez eux.
| Voisine | Nbre de fruits ( X) |
| Sam | 3 |
| Daniel | 4 |
| Rouge-gorge | 6 |
| Marie | sept |
| Kim | 9 |
Le nombre de fruits sont des points de données désignés par x et Mean est représenté par \(\bar{x}\) . La moyenne des données ci-dessus est
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Formez maintenant un tableau qui montre les points de données( \(x\) ), la moyenne ( \(\bar{x}\) ) et la différence entre le point de données et la moyenne( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7,84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0,04 |
| sept | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Trouver la moyenne des différences \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Écart-type:
\(\sigma = \sqrt{4.56} = 2.13\)
Moyenne = 5,8 fruits
Écart type = 2,13 fruits
Maintenant, nous pouvons facilement déterminer qui se trouve à moins d'un écart-type et qui est au-delà. L'écart type nous aide donc à savoir quels sont les cas normaux et quels sont les cas extraordinaires.
Nous pouvons nous attendre à ce qu'environ les deux tiers des données se situent à +1 ou -1 écart type par rapport à la moyenne. On peut dire que \(\frac{2}{3}^{rd}\) des voisins ont entre 7,93(5,8 + 2,13) et 3,67 (5,8 - 2,13) fruits dans leurs maisons.
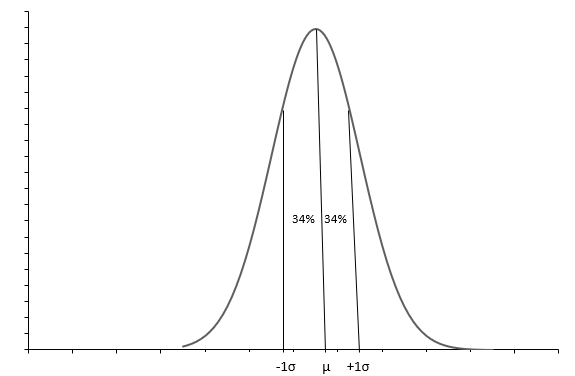
Le graphique ci-dessus montre une distribution normale avec une courbe en forme de cloche. Chaque distribution normale est définie avec la moyenne( \(\mu\) ) et l'écart type( \(\sigma\) ). Environ 68 % des observations se situent entre \(+1\sigma\) et \(-1\sigma\) . La moyenne ( \(\mu\) ) également la médiane nous indique le point médian de la distribution, autour duquel toutes les valeurs de données sont réparties. L'écart type( \(\sigma\) ) nous indique comment répartir les données.
Pour calculer l'écart type, suivez les étapes ci-dessous :
1) Trouver la moyenne ( \(\bar{x}\) ) des éléments de données dans l'ensemble donné
2) Prenez chaque différence d'élément de données de la moyenne, mettez-la au carré, puis faites la moyenne du résultat. Ce résultat est appelé Variance
3) Prenez la racine carrée de la variance, cela donnera l'écart type \(\sigma\)