विचलन का अर्थ है सामान्य या औसत से कितनी दूर।
हम मानक विचलन का उपयोग यह जानने के लिए कर सकते हैं कि कुछ व्यवहार सामान्य है या अद्वितीय/असाधारण। मानक विचलन की गणना अक्सर डेटा सेट के माध्य से की जाती है, और यह हमें यह जानने में मदद करती है कि डेटा कितना फैला हुआ है। दूसरे शब्दों में, डेटा के एक सेट में मानक विचलन हमें बताता है कि सभी विभिन्न डेटा बिंदुओं को माध्य के चारों ओर कितनी मजबूती से क्लस्टर किया जाता है। मानक विचलन को \('\sigma'\) प्रतीक द्वारा दर्शाया जाता है।
मानक विचलन की गणना आसानी से एक कैलकुलेटर, स्प्रेडशीट सॉफ़्टवेयर या गणित के सूत्रों का उपयोग करके की जा सकती है जिन्हें नीचे समझाया गया है।
आइए इसे बेहतर ढंग से समझने के लिए एक उदाहरण लेते हैं। आइए देखें कि आपके पड़ोसियों के घरों में कितने फल हैं।
| पड़ोसी | फलों की संख्या (X) |
| सैम | 3 |
| डैनियल | 4 |
| रोबिन | 6 |
| मेरी | 7 |
| किम | 9 |
फलों की संख्या डेटा बिंदु हैं जिन्हें x द्वारा दर्शाया जाता है और माध्य को \(\bar{x}\) द्वारा दर्शाया जाता है। उपरोक्त डेटा के लिए माध्य है
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
अब एक तालिका बनाएं जो डेटा बिंदु ( \(x\) ), माध्य ( \(\bar{x}\) ) और डेटा बिंदु का माध्य ( \(x - \bar{x}\) ) से अंतर दिखाती है।
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
अंतरों का माध्य ज्ञात \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
मानक विचलन:
\(\sigma = \sqrt{4.56} = 2.13\)
माध्य = 5.8 फल
मानक विचलन = 2.13 फल
अब हम आसानी से पता लगा सकते हैं कि कौन एक मानक विचलन के भीतर है और कौन इससे परे है। तो मानक विचलन हमें यह जानने में मदद करता है कि सामान्य मामले क्या हैं और असाधारण मामले क्या हैं।
हम उम्मीद कर सकते हैं कि लगभग दो-तिहाई डेटा माध्य से +1 या -1 मानक विचलन के भीतर आ जाएगा। हम कह सकते हैं कि \(\frac{2}{3}^{rd}\) पड़ोसियों के घरों में 7.93(5.8 + 2.13) और 3.67 (5.8 - 2.13) फल हैं।
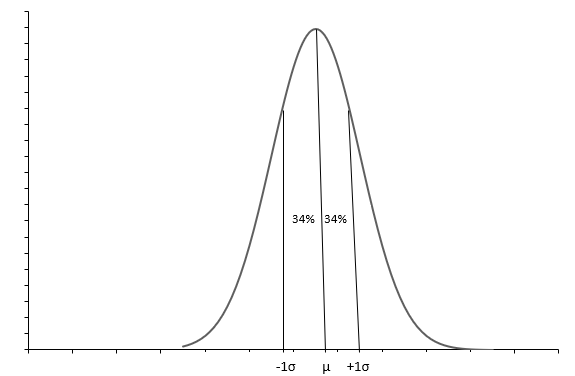
उपरोक्त ग्राफ घंटी के आकार के वक्र के साथ एक सामान्य वितरण दिखाता है। प्रत्येक सामान्य वितरण को माध्य ( \(\mu\) ) और मानक विचलन ( \(\sigma\) ) के साथ परिभाषित किया गया है। लगभग 68% अवलोकन \(+1\sigma\) और \(-1\sigma\) के बीच आते हैं। माध्य ( \(\mu\) ) भी माध्यिका हमें वितरण का मध्य-बिंदु बताता है, जिसके चारों ओर सभी डेटा मान फैले हुए हैं। मानक विचलन ( \(\sigma\) ) हमें बताता है कि डेटा को कैसे फैलाना है।
मानक विचलन की गणना करने के लिए नीचे दिए गए चरणों का पालन करें:
1) दिए गए सेट में डेटा आइटम्स का माध्य ( \(\bar{x}\) ) ज्ञात कीजिए
2) डेटा आइटम के प्रत्येक अंतर को माध्य से लें, इसे वर्ग करें, और फिर परिणाम को औसत करें। इस परिणाम को वेरिएंस कहा जाता है
3) प्रसरण का वर्गमूल लें, यह मानक विचलन देगा \(\sigma\)