Odstupanje znači koliko je daleko od normale ili prosjeka.
Možemo koristiti standardnu devijaciju da znamo je li određeno ponašanje normalno ili jedinstveno/izvanredno. Standardna devijacija se često izračunava pomoću srednje vrijednosti skupa podataka i pomaže nam da znamo koliko su podaci rašireni. Drugim riječima, u skupu podataka standardna devijacija nam govori koliko su čvrsto sve različite podatkovne točke grupirane oko srednje vrijednosti. Standardna devijacija je označena simbolom \('\sigma'\) .
Standardna devijacija može se lako izračunati pomoću kalkulatora, softvera za proračunske tablice ili matematičkih formula koje su objašnjene u nastavku.
Uzmimo primjer kako bismo to bolje razumjeli. Uzmimo u obzir broj voća koje vaši susjedi imaju u svojim kućama.
| Susjed | broj voća (X) |
| Sam | 3 |
| Daniel | 4 |
| Robin | 6 |
| Marija | 7 |
| Kim | 9 |
Broj plodova su podatkovne točke koje su označene s x, a srednja vrijednost je predstavljena s \(\bar{x}\) . Srednja vrijednost za gornje podatke je
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Sada formirajte tablicu koja prikazuje podatkovne točke ( \(x\) ), srednju vrijednost ( \(\bar{x}\) ) i razliku podatkovne točke od srednje vrijednosti ( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0,04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Pronađite srednju vrijednost razlika \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
standardna devijacija:
\(\sigma = \sqrt{4.56} = 2.13\)
Srednja vrijednost = 5,8 plodova
Standardna devijacija = 2,13 plodova
Sada možemo lako shvatiti tko je unutar jedne standardne devijacije, a tko izvan nje. Dakle, standardna devijacija nam pomaže da znamo što su normalni, a što izvanredni slučajevi.
Možemo očekivati da će oko dvije trećine podataka biti unutar +1 ili -1 standardne devijacije od srednje vrijednosti. Možemo reći da \(\frac{2}{3}^{rd}\) susjeda ima između 7,93(5,8 + 2,13) i 3,67 (5,8 - 2,13) plodova u svojim kućama.
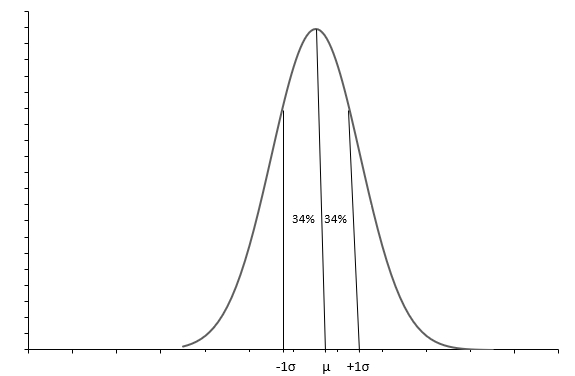
Gornji grafikon prikazuje normalnu distribuciju s krivuljom u obliku zvona. Svaka normalna distribucija definirana je srednjom ( \(\mu\) ) i standardnom devijacijom ( \(\sigma\) ). Otprilike 68% opažanja je između \(+1\sigma\) i \(-1\sigma\) . Srednja vrijednost ( \(\mu\) ) također medijan nam govori o središnjoj točki distribucije, oko koje se šire sve vrijednosti podataka. Standardna devijacija ( \(\sigma\) ) nam govori kako rasporediti podatke.
Za izračunavanje standardne devijacije slijedite sljedeće korake:
1) Pronađite srednju vrijednost ( \(\bar{x}\) ) stavki podataka u danom skupu
2) Uzmite svaku razliku podatka iz srednje vrijednosti, kvadrirajte je, a zatim usrednjujte rezultat. Ovaj rezultat se zove Variance
3) Uzmi kvadratni korijen varijance, to će dati standardnu devijaciju \(\sigma\)